Efeitos da Constante Cosmológica


Próxima: Efeitos da Constante Cosmológica
Volta: Cosmologia Relativística
Anterior: Levantando e Baixando Índices
A observação de que o Universo é homogêneo e isotrópico,
e que está em expansão segundo a lei de Hubble, produz
condições suficientes para que a Teoria da Relatividade
Geral prediga concretamente a topologia e a evolução
do Universo.
Para um sistema isotrópico e homogêneo, podemos escrever
as coordenadas em um sistema esférico, e considerar somente
a coordenada radial, que chamaremos de 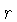 , distância média
entre as galáxias, e a coordenada temporal,
, distância média
entre as galáxias, e a coordenada temporal, 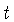 .
Pode-se demonstrar que a
componente i=0, k=0 ou i=t, k=t do tensor de Einstein
.
Pode-se demonstrar que a
componente i=0, k=0 ou i=t, k=t do tensor de Einstein 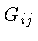 :
:
é dada por:
A condição de homogeneidade implica que a métrica deve
ser homogênea. Para uma esfera de raio r, em três dimensões,
uma geodésica é dada por:
Para uma métrica de Friedmann, onde para cada valor de 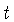 o espaço-tempo
representa um hiper-esfera quadri-dimensional de circunferência própria
o espaço-tempo
representa um hiper-esfera quadri-dimensional de circunferência própria
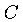 , e o locus
, e o locus
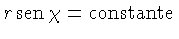 define esferas de área
define esferas de área 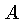 ,
temos:
A circunferência própria (
,
temos:
A circunferência própria (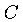 ) é dada por:
a área da superfície (
) é dada por:
a área da superfície (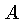 ):
e o volume (
):
e o volume (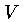 ) da quadri-esfera:
Neste caso,
A equação (24), com
) da quadri-esfera:
Neste caso,
A equação (24), com 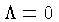 , se reduz a:
, se reduz a:
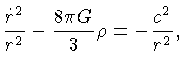 |
(1.27) |
já que pela equação (23):
Como o volume total deste Universo fechado é 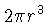 ,
identificando
,
identificando 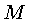 como a massa total em prótons, nêutrons,
elétrons, etc.,
como a massa total em prótons, nêutrons,
elétrons, etc.,
e a equação (27) pode ser escrita como:
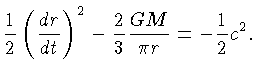 |
(1.28) |
Fazendo a mudança para variáveis adimensionais
a equação (28) pode ser re-escrita como:
que nós já resolvemos com a solução da equação (14)
para o caso do Universo fechado.
A densidade total é dada por:
Quando o Universo está dominado por matéria,
onde
e como:
Quando o Universo era dominado pela radiação:
onde
e
Podemos expandir a equação (27) para 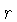 pequeno em:
e integrar, assumindo
pequeno em:
e integrar, assumindo 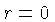 para
para 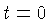 ,
ou seja,
,
ou seja,
O físico-matemático americano
Howard Percy Robertson (1894-1979)
e o matemático inglês Arthur Geoffrey Walker (1909-2001),
demonstraram em 1935 e 1936 que a métrica
mais geral que satisfaz a condição de homogeneidade e isotropia
para a geometria do espaço-tempo é a chamada métrica de
Robertson-Walker:
Esta métrica pode ser convertida para a forma de Friedmann,
com um fator de renormalização.
Para a métrica de Robertson-Walker, a componente (00) da
equação de campo de Einstein se reduz a:
Como na Equação (3), podemos identificar a
constante de Hubble como:
A trajetória de uma galáxia que se move junto com a expansão
do Universo é dada por (r,θφ)=
constante, enquanto
que a trajetória de um fóton satisfaz
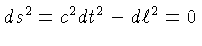 .
Portanto a distância
.
Portanto a distância 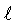 que um fóton percorre afastando-se
radialmente (θ e φ
mantidos constantes) de uma fonte
é governada pela equação diferencial:
que um fóton percorre afastando-se
radialmente (θ e φ
mantidos constantes) de uma fonte
é governada pela equação diferencial:
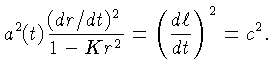 |
(1.29) |
Logo of fótons sempre atravessam uma distância própria 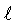 em um intervalo de tempo próprio
em um intervalo de tempo próprio 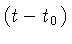 à velocidade da luz
à velocidade da luz 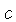 ,
Após ser emitido por uma fonte isotrópica, o fóton atravessa
uma esfera de área
,
Após ser emitido por uma fonte isotrópica, o fóton atravessa
uma esfera de área
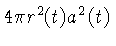 em um tempo
em um tempo 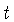 , mas esta
área não é igual a
, mas esta
área não é igual a
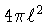 , pois depende do valor de
, pois depende do valor de
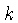 e de
e de 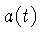 .
.
Por exemplo, para um Universo de Einstein-de Sitter, isto é, plano,
K=0 e
Se o fóton for emitido num tempo te,
o desvio para o vermelho (redshift) z
na recepção (tempo t0) será dado por:
A equação (29), para K=0, se reduz a:
de modo que
onde
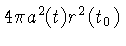 é a área da esfera centrada na fonte e
passando pelo tempo presente. Como
é a área da esfera centrada na fonte e
passando pelo tempo presente. Como
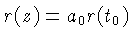 ,
já que para o Universo plano
,
já que para o Universo plano
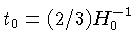 .
Tendo em vista que Universo plano é Euclidiano, r(z)
é a distância no presente da fonte,
também chamada de distância comóvel, ou distância radial própria.
A distância própria comóvel, que leva em conta que o Universo se expandiu
desde que a radiação do fundo do Universo foi emitida na época da recombinação, é de 45,7 bilhões de anos-luz, enquanto a
distância própria até a borda do Universo (após inflação, se houve) é de 46,6 bilhões de anos-luz, 2% maior
(Distance measures in cosmology, 2000, de
David W. Hogg,
A Map of the Universe, 2005, de
J. Richard Gott, III, Mario Juriĉ, David Schlegel, Fiona Hoyle, Michael Vogeley, Max Tegmark, Neta Bahcall, Jon Brinkmann).
Estes valores assumem os valores atuais para a constante de Hubble H0,
a constante cosmológica Λ, a densidade de energia em radiação ρr,
a densidade de matéria bariônica e escura ρm e K=0 (Universo plano).
Se a inflação ocorreu, o valor de aceleração H da época era muito maior do que o atual.
.
Tendo em vista que Universo plano é Euclidiano, r(z)
é a distância no presente da fonte,
também chamada de distância comóvel, ou distância radial própria.
A distância própria comóvel, que leva em conta que o Universo se expandiu
desde que a radiação do fundo do Universo foi emitida na época da recombinação, é de 45,7 bilhões de anos-luz, enquanto a
distância própria até a borda do Universo (após inflação, se houve) é de 46,6 bilhões de anos-luz, 2% maior
(Distance measures in cosmology, 2000, de
David W. Hogg,
A Map of the Universe, 2005, de
J. Richard Gott, III, Mario Juriĉ, David Schlegel, Fiona Hoyle, Michael Vogeley, Max Tegmark, Neta Bahcall, Jon Brinkmann).
Estes valores assumem os valores atuais para a constante de Hubble H0,
a constante cosmológica Λ, a densidade de energia em radiação ρr,
a densidade de matéria bariônica e escura ρm e K=0 (Universo plano).
Se a inflação ocorreu, o valor de aceleração H da época era muito maior do que o atual.
A distância que o fóton atravessou desde que foi emitido,
chamada de distância de viagem da luz, é dada por:
e portanto uma fonte com alto valor de z
está mais
longe do que a distância atravessada pela luz.
Definindo a pressão de cada componente como 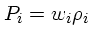 ,
,
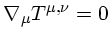 implica que
a densidade será expressa
como
implica que
a densidade será expressa
como
e o parametro de desaceleração
e
para um universo dominado por matéria e constante cosmológica,
já que 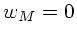 ,
,
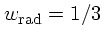 e
e 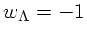 .
.
A radiação do fundo do Universo é normalmente decomposta em
esféricos harmônicos
e o momentum de multipolo é dado por
relacionado à separação angular
O valor de 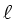 do primeiro "pico Doppler",
um aumento na potência devido a oscilações acústicas,
é diretamente proporcional ao valor de
do primeiro "pico Doppler",
um aumento na potência devido a oscilações acústicas,
é diretamente proporcional ao valor de
 ,
pois é a escala angular subentendida pelo raio de Hubble quando os
fótons da radiação de fundo se originaram, na época da recombinação.
,
pois é a escala angular subentendida pelo raio de Hubble quando os
fótons da radiação de fundo se originaram, na época da recombinação.


Próxima: Evolução Térmica
Volta: Cosmologia Relativística
Anterior: Levantando e Baixando Índices
©
Modificada em 3 jan 2019
![]() , distância média
entre as galáxias, e a coordenada temporal,
, distância média
entre as galáxias, e a coordenada temporal, ![]() .
Pode-se demonstrar que a
componente i=0, k=0 ou i=t, k=t do tensor de Einstein
.
Pode-se demonstrar que a
componente i=0, k=0 ou i=t, k=t do tensor de Einstein ![]() :
:
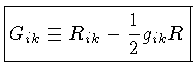
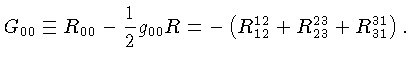
![ds^2 = c^2dt^2 - r(t)[d\chi^2 + sen^2 \chi\,(d\theta^2 + sen^2 \theta d\phi^2)]](img2601.gif)
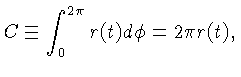
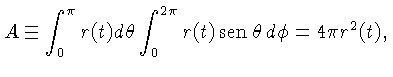
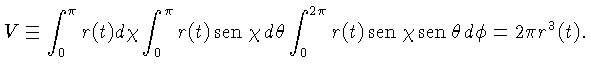
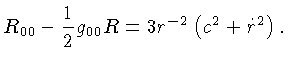
![]() ,
identificando
,
identificando ![]() como a massa total em prótons, nêutrons,
elétrons, etc.,
como a massa total em prótons, nêutrons,
elétrons, etc.,
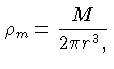
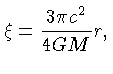
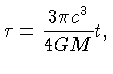
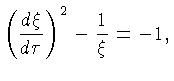
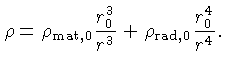
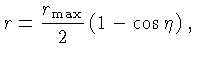
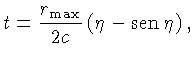
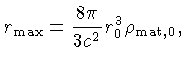
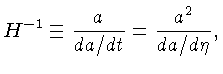
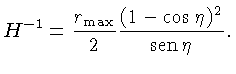
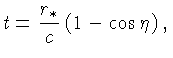
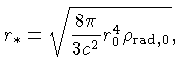
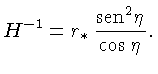
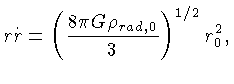
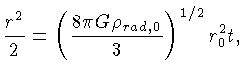
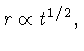
![${ds^2 = c^2dt^2 - a^2(t)[\frac{dr^2}{1-Kr^2} + r^2(d\theta^2 + sen^2 \theta d\phi^2)]}$](img279.gif)
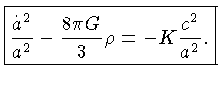
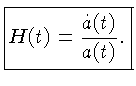
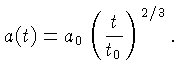
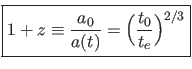
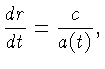
![$r(t_0)=\frac{3c}{a_0}t_0[1-(\frac{t_e}{t_0})^{1/3}]$](img298.gif)
![$r(z)=\frac{2c}{H_0}\left[1-(1+z)^{-\frac{1}{2}}\right],$](img301.gif)
![$\ell(z)=c(t_e-t_0) = \frac{2c}{3H_0}[1-(1+z)^{-\frac{1}{2}}]$](img304.gif)
![]() ,
,
![]() implica que
a densidade será expressa
como
implica que
a densidade será expressa
como
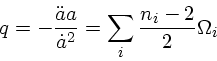
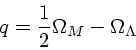
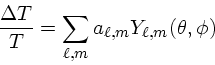
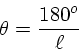
![]() do primeiro "pico Doppler",
um aumento na potência devido a oscilações acústicas,
é diretamente proporcional ao valor de
do primeiro "pico Doppler",
um aumento na potência devido a oscilações acústicas,
é diretamente proporcional ao valor de
![]() ,
pois é a escala angular subentendida pelo raio de Hubble quando os
fótons da radiação de fundo se originaram, na época da recombinação.
,
pois é a escala angular subentendida pelo raio de Hubble quando os
fótons da radiação de fundo se originaram, na época da recombinação.