Tempo Conformal e Raio do Universo
Considerando a métrica de Friedmann-Lemaître-Robertson-Walker [Howard Percy Robertson (1903-1961), 1935;
Arthur Geoffrey Walker (1909-2001), 1937;
Georges Henri Joseph Edouard Lamaître (1894-1966), 1927; Alexander Alexandrovich Friedmann (Алекса́ндр Алекса́ндрович Фри́дман, 1888-1925), 1922]
em coordenadas polares reduzidas a uma circunferência
ds2 = -
c2dt2 +
R2(
t)
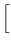
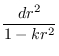
+
r2(
dθ2 + sen
2θdφ2![$ \Big]$](img3.png)
onde t é o tempo cosmológico desde o Big Bang (ou fim da inflação, se houve),
R(t) é o fator de escala, ou raio de curvatura,
a(t) = R(t)/R0 é o fator de escala
adimensional, as galáxias individuais participam da expansão cósmica seguindo uma geodésica
com valores constantes de r, θ e φ, as coordenadas de comovimento,
e k=-1,0,1 é o sinal da curvatura espacial, para universo aberto, plano ou fechado.
Por esta definição de a(t), a=1 no presente, mas atente para a mudança de normalização ao calcularmos o raio de curvatura para o Universo plano.
Definindo o tempo conformal η pela relação
dη = dt/a
η(
t) =
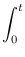
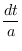
de modo que a luz viaja em geodésicas radiais com
c dη = ±dr. Deste modo, uma galáxia a
uma distância comóvel r de nós emitiu a luz que vemos hoje em um tempo conformal
η(t) = η(t0) - r/c.
Desta forma podemos calcular o tempo t e o desvio para o vermelho (redshift)
z =
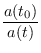
- 1
quando a luz foi emitida.
Como os fótons viajam em geodésicas nulas de tempo próprio nulo,
r =
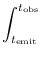 c
c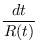
a distância comóvel é constante.
O fator de escala
a(t) = a(t0)/(1 + z) obedece
para qualquer valor de K,
ρm∝a-3 é a densidade de matéria, incluindo a matéria escura fria,
ρr∝a-4 é a densidade de radiação média do Universo, principalmente vindo da radiação do
fundo do Universo,
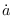 = a, t é a derivada de a em relação ao tempo. Esta equação é chamada Equação de Friedmann.
= a, t é a derivada de a em relação ao tempo. Esta equação é chamada Equação de Friedmann.
Podemos escrever
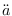 = a„ tt a segunda derivada e, portanto,
a aceleração da expansão
= a„ tt a segunda derivada e, portanto,
a aceleração da expansão
mostrando que a constante cosmológica produz aceleração, enquanto a densidade de matéria e de radiação
produzem desaceleração.
O tempo conformal pode ser obtido integrando-se a equação de Friedman
c η(
t) =
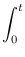 c
c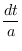
=
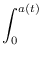
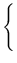
-
Ka2 +
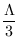 a4
a4 +
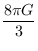 a4
a4[
ρm(
a) +
ρr(
a)]
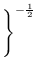 da
da
A Lei de Hubble é escrita como
Note que a(t) é o raio de curvatura do Universo para K = ±1,
mas para K = 0 não existe esta escala e podemos renormalizar colocando
a0 = a(t0)≡RH0 = cH0-1 = 4220 Mpc, para H0 = 71 km/s/Mpc. Note que esta normalização é diferente da anterior.
Desta forma η mede as distâncias comóveis na época atual, em unidades do radio de Hubble atual, RH0.
Para Universo plano, K=0,
c η(
a) =
c η[
a(
t)] =
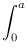
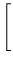
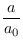 Ωm
Ωm +
Ωr +
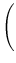
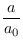
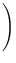 ΩΛ
ΩΛ![$ ]^{{-\frac{1}{2}}}_{}$](img31.png)
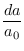
que com os valores atuais resulta em
c η(a0) = 3,38
indicando que quando olhamos agora em t = t0, podemos enxergar até uma distância comóvel de
c η(a0)a0 = 14 300 Mpc=46,6 bilhões de anos-luz.
Este é o horizonte de partículas efetivo, onde estão as partículas do momento do Big Bang (ou fim da inflação, se houve).
Esta distância é maior do que a idade do Universo, porque é a distância comóvel que as partículas mais velhas terão agora,
e não a distância que tinham então.
Podemos calcular esta distância em função de a, ou em função de z. Para
zrecomb = 1089,
c η(zrecomb) = 0.0671 a0 e, portanto,
a distância comóvel da radiação do
fundo do Universo é
[c(η0 - η(zrecomb)]a0 = 14 000 Mpc
A idade do Universo pode ser escrita como
t(
z) =
H(
z)
-1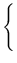
[1 -
Ω(
z)]
-1 +
![$ {\frac{{K \Omega(z)}}{{2[K(\Omega(z)-1)]^{3/2}}}}$](img33.png) CK-1
CK-1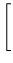
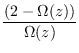
![$ r]$](img36.png)
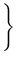
onde o parâmetro de densidade total Ω
ρcr tico
tico =
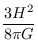
Como ρ e H mudam com o tempo, o parâmetro de densidade depende da época,
mas Ω = 1 é constante para Universo plano (K=0).
ρΛ =
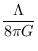
Inserindo a dependencia de z em H(z) e Ω(z) para o caso geral,
H(
z) =
H0(1 +
z)
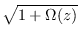
Ω(
z) =
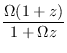
nos dá a relação tempo-desvio para o vermelho,
que pode ser aproximada por
Ck(
r) =
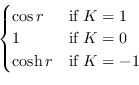
O valor presente do fator de escala, para K = ±1, é obtido diretamente da equação de Friedmann:
 Cosmologia na Relatividade Geral
Cosmologia na Relatividade Geral
 Cosmologia Matemática
Cosmologia Matemática
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 5 jan 2019
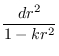 + r2(dθ2 + sen2θdφ2
+ r2(dθ2 + sen2θdφ2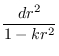 + r2(dθ2 + sen2θdφ2
+ r2(dθ2 + sen2θdφ2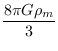 +
+ 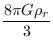
![]() = a„ tt a segunda derivada e, portanto,
a aceleração da expansão
= a„ tt a segunda derivada e, portanto,
a aceleração da expansão
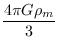 -
- 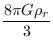
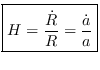
![$ {\frac{{K \Omega(z)}}{{2[K(\Omega(z)-1)]^{3/2}}}}$](img33.png) CK-1
CK-1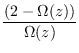
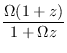
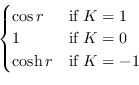
![$ {R_0=\frac{c}{H_0}[\frac{(\Omega-1)}{k}]^{-\frac{1}{2}}}$](img50.png)
![]()