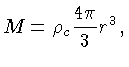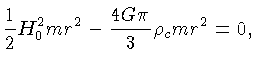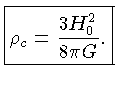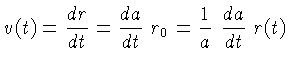

Próxima: Idade do Universo
Volta: Cosmologia Newtoniana
Anterior: Cosmologia Newtoniana
Consideremos uma galáxia de massa 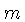 movendo-se com
velocidade
movendo-se com
velocidade 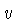 ,
a uma distância
,
a uma distância 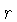 de um sistema de coordenadas qualquer,
em um sistema de massa total
de um sistema de coordenadas qualquer,
em um sistema de massa total 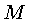 contida no volume de raio
contida no volume de raio 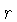 .
A energia total do sistema, na ausência de cargas elétricas,
é a soma da energia cinética
com a energia potencial gravitacional:
.
A energia total do sistema, na ausência de cargas elétricas,
é a soma da energia cinética
com a energia potencial gravitacional:
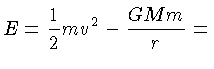
constante

Dependendo do valor da energia total do Universo,
que é uma constante do sistema,
o Universo será aberto ou fechado.
Usando a lei de Hubble:
onde 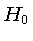 é a constante de Hubble no presente, e
onde
é a constante de Hubble no presente, e
onde 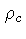 é a densidade crítica, isto é,
a densidade necessária para parar a expansão do Universo,
é a densidade crítica, isto é,
a densidade necessária para parar a expansão do Universo,
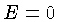 , obtemos:
Usando
, obtemos:
Usando 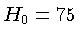 km/s/Mpc, obtemos
que pode ser comparado com a densidade de matéria visível
observada, que é da ordem de
km/s/Mpc, obtemos
que pode ser comparado com a densidade de matéria visível
observada, que é da ordem de
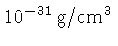 ,
ou seja, cerca de 100 vezes menor do que a densidade crítica.
,
ou seja, cerca de 100 vezes menor do que a densidade crítica.
Vamos escrever a distância
entre dois pontos quaisquer no espaço como:
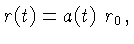 |
(1.1) |
onde 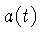 é um fator de escala crescente com o tempo para um Universo
em expansão e
é um fator de escala crescente com o tempo para um Universo
em expansão e 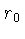 é a distância entre os dois pontos no instante
é a distância entre os dois pontos no instante
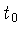 em que
em que
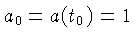 .
.
A velocidade de recessão entre os dois pontos pode ser obtida
derivando-se (1) no tempo:
Se escrevermos:
 |
(1.2) |
como na lei de Hubble, identificamos
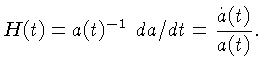 |
(1.3) |


Próxima: Idade do Universo
Volta: Cosmologia Newtoniana
Anterior: Cosmologia Newtoniana
©
Modificada em 6 fev 1999
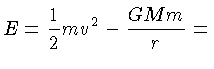 constante
constante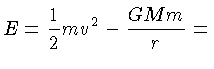 constante
constante