
 Limite de Eddington
Polítropos são modelos para os casos em que a pressão pode ser
escrita como uma função que depende somente da densidade. Nestes
casos específicos, como para gases degenerados, podemos calcular
analiticamente as relações entre pressão, massa e raio.
Quando vamos calcular modelos estelares, necessitamos de
valores iniciais de pressão central e raio estelar, por exemplo.
Como podemos estimar estes valores? Em geral usam-se modelos
de polítropos para estes valores iniciais.
Os polítropos são adequados para situações especiais, como no
caso de anãs brancas e estrelas no Ramo Gigante
e Supergigante.
Limite de Eddington
Polítropos são modelos para os casos em que a pressão pode ser
escrita como uma função que depende somente da densidade. Nestes
casos específicos, como para gases degenerados, podemos calcular
analiticamente as relações entre pressão, massa e raio.
Quando vamos calcular modelos estelares, necessitamos de
valores iniciais de pressão central e raio estelar, por exemplo.
Como podemos estimar estes valores? Em geral usam-se modelos
de polítropos para estes valores iniciais.
Os polítropos são adequados para situações especiais, como no
caso de anãs brancas e estrelas no Ramo Gigante
e Supergigante.
Quando discutimos a equação de estado
de um gás completamente degenerado,
não-relativístico,
obtivemos:
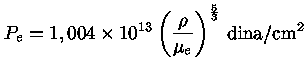 |
(1) |
que é uma lei de potência com
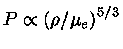 .
.
Outra situação é para uma estrela
completamente convectiva,
com
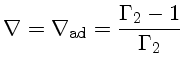 .
Como
.
Como
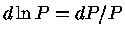 e
e
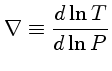
|
(2) |
Integrando-se,
obtemos
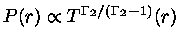 |
(3) |
Se o gás for ideal,
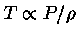 e portanto
e portanto
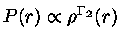 .
.
Como nesses exemplos,
se a pressão puder ser escrita como uma função da densidade
somente, 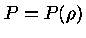 , então a estrutura da estrela depende
somente das equações de equilíbrio hidrostático
e continuidade da massa.
Em particular, se a pressão em todos os pontos do interior
estelar satisfizer a relação
, então a estrutura da estrela depende
somente das equações de equilíbrio hidrostático
e continuidade da massa.
Em particular, se a pressão em todos os pontos do interior
estelar satisfizer a relação
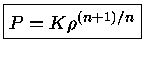 |
(4) |
com 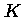 e
e 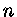 constantes, a configuração é chamada de
um polítropo.
constantes, a configuração é chamada de
um polítropo.
Para um gás ideal,
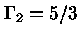 ,
e
,
e 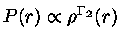 de uma estrela
completamente convectiva nos dá
de uma estrela
completamente convectiva nos dá
Note que este é o mesmo expoente
do gás completamente degenerado, não relativístico.
As equações de equilíbrio hidrostático
e continuidade da massa podem ser reduzidas a uma equação
diferencial de segunda ordem, dividindo-se a equação
de equilíbrio hidrostático por 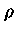 ,
multiplique por
,
multiplique por 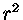 e, então, derivando-se em relação
a
e, então, derivando-se em relação
a 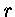 os dois lados:
os dois lados:
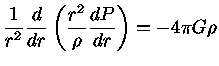 |
(5) |
que é a equação de Poisson.
Se definirmos variáveis adimensionais
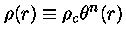 |
(6) |
e
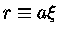 |
(7) |
onde
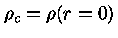 é a densidade central e a constante
é a densidade central e a constante 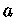 dada pela equação
dada pela equação
![$ a = [\frac{(n+1)K\rho_c^{(1/n-1)}}{4\pi G}]^\frac{1}{2}$](img23.gif) |
(8) |
a equação de Poisson
(equação 5) pode ser escrita como
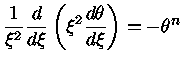 |
(9) |
Essa equação é chamada de equação de Lane-Emden, em honra ao
físico americano Jonathan Homer Lane
(1819-1880), que derivou a equação do
equilíbrio hidrostático em 1869 e ao
físico suíço Robert Emden (1862-1940).
Modelos correspondentes às soluções dessa equação,
para um certo valor de 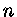 ,
são chamados de polítropos de índice
,
são chamados de polítropos de índice 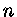 .
A pressão será dada por
.
A pressão será dada por
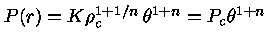 |
(10) |
Se a equação de estado do material for a de um gás ideal,
com
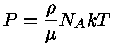 |
(11) |
então
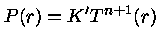 |
(12) |
e
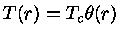 |
(13) |
com
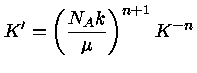 |
(14) |
e
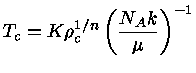 |
(15) |
Portanto, para um polítropo com equação de estado de gás
ideal e 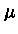 constante,
constante, 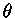 mede a temperatura. Finalmente, nesse
caso, o fator de escala radial é dado por
mede a temperatura. Finalmente, nesse
caso, o fator de escala radial é dado por
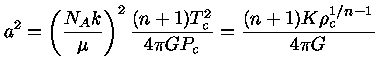 |
(16) |
As condições de contorno
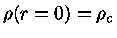 e
e
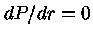 para
para 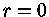 se traduzem em
se traduzem em
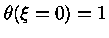 e
e
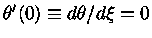 . Se o índice
politrópico
. Se o índice
politrópico 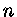 e a densidade central
e a densidade central 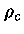 forem dados,
podemos integrar a equação de Lane-Emden (equação 9)
numericamente do centro até uma distância
forem dados,
podemos integrar a equação de Lane-Emden (equação 9)
numericamente do centro até uma distância 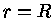 onde
onde 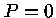 .
Se chamarmos de
.
Se chamarmos de
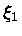 a variável radial onde
a variável radial onde
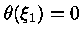 para
para 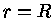 , obtemos para o valor do raio
, obtemos para o valor do raio
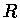 :
:
![$ R = a\xi_1 = [\frac{(n+1)P_c}{4\pi G \rho^2_c}]^\frac{1}{2} \xi_1$](img45.gif) |
(17) |
Dessa forma, especificando
K, n e ρ, ou Pc,
obtemos o raio R.
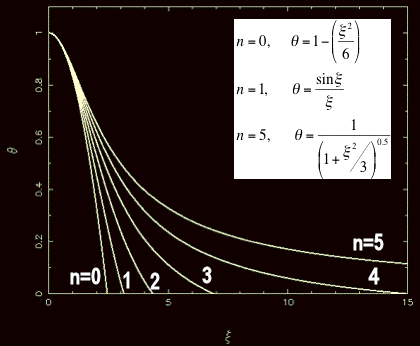 Solução analíticas existem para
n=0, 1 e 5. Soluções
numéricas precisam ser obtidas para um valor de
n geral.
A solução para n=0
corresponde a uma esfera de densidade constante,
e
Solução analíticas existem para
n=0, 1 e 5. Soluções
numéricas precisam ser obtidas para um valor de
n geral.
A solução para n=0
corresponde a uma esfera de densidade constante,
e
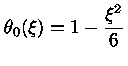 |
(18) |
com
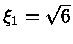 . Nesse caso
. Nesse caso
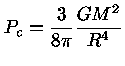 |
(19) |
Para n=1 a solução
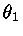 é a função sinc
é a função sinc
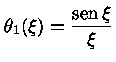 |
(20) |
com
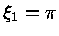 . A densidade é dada por
. A densidade é dada por
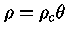 e a pressão por
e a pressão por
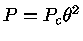 .
.
O polítropo para n=5 tem uma densidade central finita, mas o raio
é ilimitado
![$ \theta_5(\xi) = [1+\xi^2/3]^{-\frac{1}{2}}$](img57.gif) |
(21) |
com
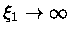 . Apesar de ter raio infinito, o polítropo
contêm uma quantidade de massa finita. As soluções com
. Apesar de ter raio infinito, o polítropo
contêm uma quantidade de massa finita. As soluções com 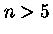 também
são infinitas em raio, mas contém também massa infinita. O intervalo de interesse, portanto, está limitado para
também
são infinitas em raio, mas contém também massa infinita. O intervalo de interesse, portanto, está limitado para
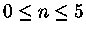 .
.
A massa contida em uma esfera de raio r
pode ser obtida pela equação
da continuidade da massa
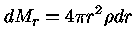 |
(22) |
Em termos de 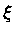 , obtemos
, obtemos
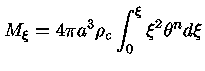 |
(23) |
Pela equação de Lane-Emden (equação 9),
podemos substituir 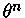 por
por
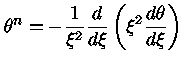 |
(24) |
eliminando o fator 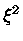 e a própria integral, obtendo
e a própria integral, obtendo
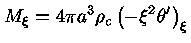 |
(25) |
onde
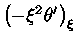 significa calcular
significa calcular
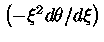 no ponto
no ponto 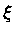 . A massa
total é dada por
. A massa
total é dada por
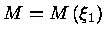 e
e
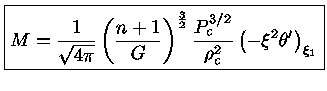 |
(26) |
Com alguma álgebra, pode-se chegar a
Se a equação de estado for de um gás ideal
Para cada valor de 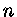 , podemos obter
, podemos obter
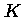 em função de
em função de 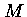 e
e 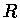 :
:
![$ K = [\frac{4\pi}{\xi^{n+1} (-\theta')^{n-1}}]^{\frac{1}{n}}_{\xi_1} \frac{G}{n+1}M^{1-1/n}R^{-1+3/n}$](img80.gif) |
(31) |
Note que se n=3, 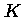 depende somente de
depende somente de 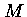 .
.
Uma outra quantidade útil é a densidade média
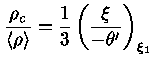 |
(32) |
Os valores de 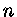 que nos interessam são n=3/2,
para o caso de um gás completamente degenerado mas não
relativístico,
que nos interessam são n=3/2,
para o caso de um gás completamente degenerado mas não
relativístico,
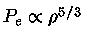 , que também
é o caso de um gás ideal completamente convectivo,
e
, que também
é o caso de um gás ideal completamente convectivo,
e 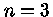 para um gás totalmente relativístico
para um gás totalmente relativístico
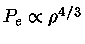 .
.
As soluções numéricas nestes casos estão listados na
Tabela (1).
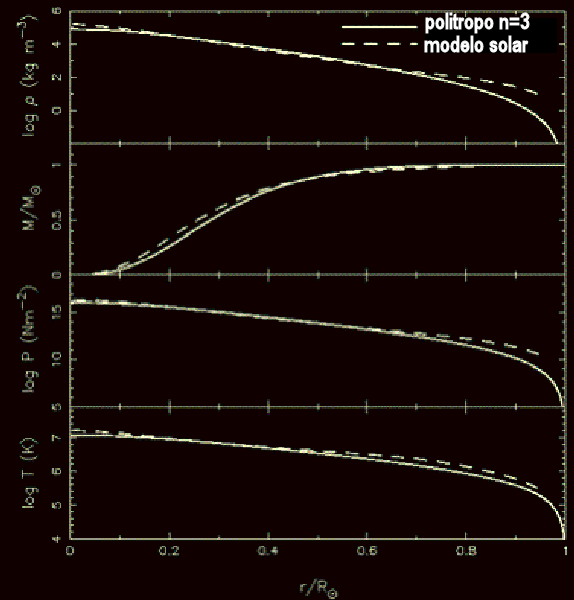
Um polítropo com a massa e o raio do Sol e n=3 tem
ρ
c=7.65×10
4 kg/m
3
e
P
c=1.25×10
16 N/m
2,
enquanto um modelo do Sol tem
ρ
c=1.52×10
5 kg/m
3
e
P
c=2.34×10
16 N/m
2.
Um gás completamente degenerado
mas não-relativístico
pode ser representado por um polítropo de ordem 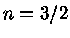 . Além disso,
a comparação
da relação entre pressão e densidade de um
polítropo
(equação 4)
com a equação da pressão
degenerada não-relativística
(equação 1)
mostra que
. Além disso,
a comparação
da relação entre pressão e densidade de um
polítropo
(equação 4)
com a equação da pressão
degenerada não-relativística
(equação 1)
mostra que
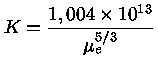 |
(33) |
Mas se usarmos o valor da constante K dado pela
equação (31),
com o valor do coeficiente θ′
dado pela tabela (1), obtemos
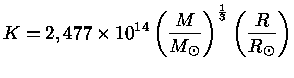 |
(34) |
Substuindo (33) em (34) obtemos
a relação massa-raio das anãs brancas:
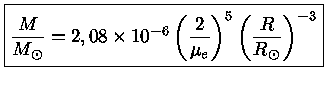 |
(35) |
Vemos que para um gás completamente degenerado, o raio é menor quanto maior
for a massa e, pelo princípio da incerteza, maior é a velocidade dos
elétrons.
Para o limite
completamente degenerado e relativístico, encontramos
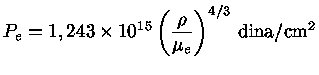 |
(36) |
Portanto, trata-se de um polítropo com 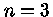 .
Usando a constante K
dada pela equação (31),
com o valor do coeficiente θ′
dado pela tabela (1) nos dá
.
Usando a constante K
dada pela equação (31),
com o valor do coeficiente θ′
dado pela tabela (1) nos dá
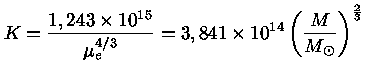 |
(37) |
ou
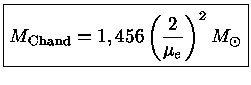 |
(38) |
que é a massa limite de Chandrasekhar, a maior massa
que uma anã branca pode alcançar, pois neste caso a velocidade
dos elétrons é igual à velocidade da luz!
Para estrelas de altíssima massa, a pressão de radiação domina.
Calculemos quando a pressão de radiação é igual à gravidade
local; para qualquer valor de radiação acima desse limite, não
haverá equilíbrio hidrostático, havendo excessiva perda de massa.
Pela equação do equilíbrio hidrostático, substituindo a
pressão total pela pressão de radiação:
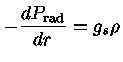 |
(39) |
A equação do transporte radiativo é dada por
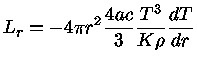 |
(40) |
e a pressão de radiação por
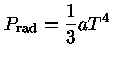 |
(41) |
Portanto, derivando a equação (41) em relação a 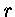 , obtemos
, obtemos
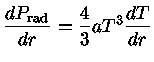 |
(42) |
ou seja, podemos escrever a equação (40) como
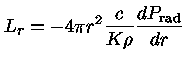 |
(43) |
Substituindo o último termo pela equação (39), obtemos
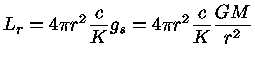 |
(44) |
chegando-se ao limite de Eddington, que representa a maior luminosidade
que uma estrela de massa 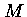 pode ter em equilíbrio
hidrostático:
pode ter em equilíbrio
hidrostático:
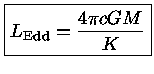 |
(45) |
Como para altas temperaturas a opacidade K
é dominada pelo
espalhamento de elétrons,
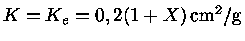 ,
podemos estimar, para X=0,7:
,
podemos estimar, para X=0,7:
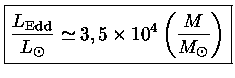 |
(46) |
Na verdade, se a luminosidade for alguns décimos da luminosidade
de Eddington, a pressão de radiação será tão intensa
que haverá perda de massa significativa.
Se dividirmos a
relação entre a massa e a luminosidade na
seqüência principal
pela equação (46) obtemos
ou seja
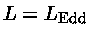
para
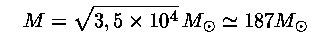
Esta é a maior massa para uma estrela na seqüência principal.
Sir Arthur Stanley Eddington (1882-1944),
no seu livro "A Constituição Interna
das Estrelas" de 1929, já propôs que as
estrelas acima de uma certa massa sofreriam pulsações
que as tornariam instáveis, limitando suas massas.
O limite derivado acima, com a opacidade dada por
espalhamento de elétrons, é maior do
que o observado, pois o vento é dominado pela opacidade
das linhas metálicas, como mostrado por
Henny J.G.L.M. Lamers (1941-) & Edward L. Fitzpatrick em 1988,
no Astrophysical Journal, 324, 279.
É interessante notar que embora as estrelas tipo O sejam intrínsecamente
mais luminosas, como a maior parte da radiação é emitida no ultravioleta,
as estrelas A7 supergiantes são mais luminosas no visível.
Note também que durante a seqüência principal, o vento de uma estrela
de 100 massas solares contribui cerca de 2 × 1051
ergs,
mais do que os cerca de 1051
ergs despejados no meio
interestelar por uma supernova tipo II.


 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 7 set 2011
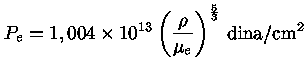
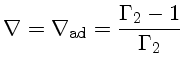 .
Como
.
Como
![]() e
e
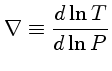
![]() , então a estrutura da estrela depende
somente das equações de equilíbrio hidrostático
e continuidade da massa.
Em particular, se a pressão em todos os pontos do interior
estelar satisfizer a relação
, então a estrutura da estrela depende
somente das equações de equilíbrio hidrostático
e continuidade da massa.
Em particular, se a pressão em todos os pontos do interior
estelar satisfizer a relação
![]() ,
e
,
e ![]() de uma estrela
completamente convectiva nos dá
de uma estrela
completamente convectiva nos dá
![]() ,
multiplique por
,
multiplique por ![]() e, então, derivando-se em relação
a
e, então, derivando-se em relação
a ![]() os dois lados:
os dois lados:
![$ a = [\frac{(n+1)K\rho_c^{(1/n-1)}}{4\pi G}]^\frac{1}{2}$](img23.gif)
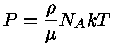
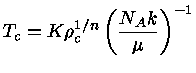
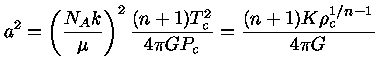
![$ R = a\xi_1 = [\frac{(n+1)P_c}{4\pi G \rho^2_c}]^\frac{1}{2} \xi_1$](img45.gif)
 Solução analíticas existem para
n=0, 1 e 5. Soluções
numéricas precisam ser obtidas para um valor de
n geral.
A solução para n=0
corresponde a uma esfera de densidade constante,
e
Solução analíticas existem para
n=0, 1 e 5. Soluções
numéricas precisam ser obtidas para um valor de
n geral.
A solução para n=0
corresponde a uma esfera de densidade constante,
e
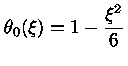
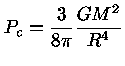
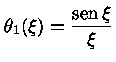
![$ \theta_5(\xi) = [1+\xi^2/3]^{-\frac{1}{2}}$](img57.gif)
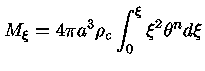
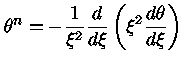
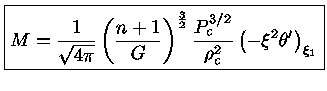
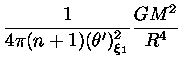
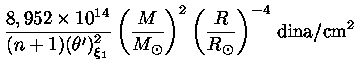
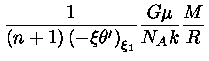
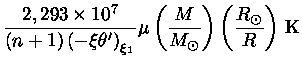
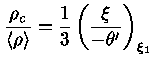

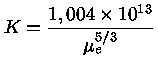
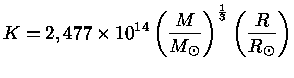
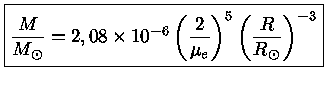
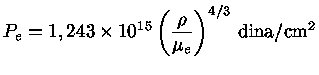
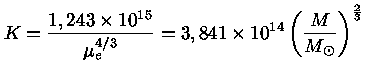
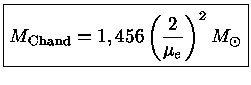
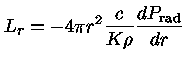
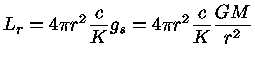
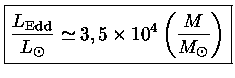
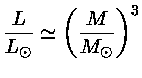
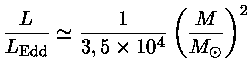
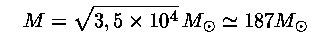
![]()