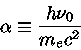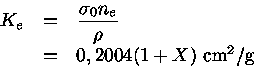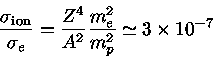Próxima: Coeficiente Total
Volta: Opacidades
Anterior: Coeficiente de Absorção Monocromática
Quando uma onda eletromagnética passa por um elétron, o campo
elétrico faz o elétron oscilar. Um elétron oscilando
representa um dipolo clássico (carga em movimento), que irradia
em todas as direções, isto é, o elétron espalha
parte da energia da onda incidente.
O tratamento clássico, chamado de espalhamento Thomson, é
válido para
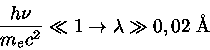 |
(1) |
Nesse caso, a energia irradiada por um elétron com aceleração
a é dada pela
equação de Larmor:
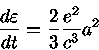 |
(2) |
Se o campo elétrico da radiação incidente for representado por
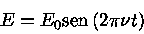 |
(3) |
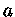 será dado por:
será dado por:
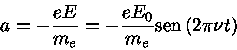 |
(4) |
de modo que
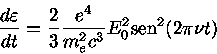 |
(5) |
Como a energia incidente por unidade de área é dada por
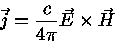 |
(6) |
onde H é o campo magnético, perpendicular e de mesma magnitude
que o campo elétrico E, temos
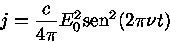 |
(7) |
e a seção de choque do espalhamento Thomson é dada por
Para o espalhamento Thomson, o coeficiente de absorção monocromático
por unidade de massa é
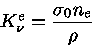 |
(10) |
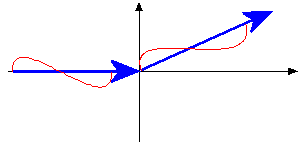
Se o elétron for acelerado para velocidades relativísticas,
precisamos utilizar as fórmulas do espalhamento de Compton,
e o espalhamento será incoerente, isto é, a radiação
emitida pelos elétrons terá uma freqüência
![\nu = \nu_0 [1-\frac{\alpha(1-\cos\theta)}{1+\alpha(1-\cos\theta)}]](opac/img15.gif) |
(11) |
onde 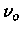 é a freqüência da radiação incidente,
é a freqüência da radiação incidente,
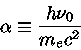 |
(12) |
e 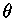 o ângulo entre o feixe incidente e a direção
do feixe irradiado.
o ângulo entre o feixe incidente e a direção
do feixe irradiado.
Para um gás completamente ionizado, a densidade de elétrons é dada
por
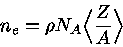 |
(13) |
Se
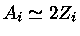 ,
,
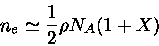 |
(14) |
e o coeficiente de absorção por unidade de massa
O espalhamento por íons é sempre menor do que o por elétrons,
pois, como têm massa mais alta, os íons respondem menos às
oscilações impostas:
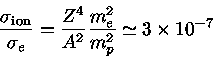 |
(15) |





Próxima: Coeficiente Total
Volta: Opacidades
Anterior: Coeficiente de Absorção Monocromática
©
Modificada em 28 ago 2011

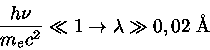
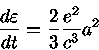
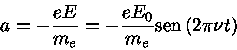
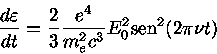
![\nu = \nu_0 [1-\frac{\alpha(1-\cos\theta)}{1+\alpha(1-\cos\theta)}]](opac/img15.gif)