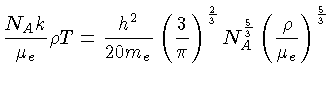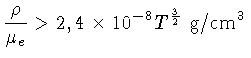Próxima: Degenerescência Total Relativística
Volta: Degenerescência dos Elétrons
Anterior: Degenerescência Total
Se a energia associada ao momentum 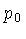 for muito menor
do que a energia de repouso do elétron,
for muito menor
do que a energia de repouso do elétron,
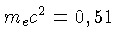 MeV,
então
MeV,
então 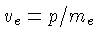 para todos os momenta na distribuição,
e a integral da pressão (1.7) é diretamente:
para todos os momenta na distribuição,
e a integral da pressão (1.7) é diretamente:
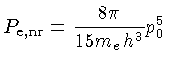 |
(1.13) |
onde nr significa elétrons não-relativísticos.
Usando a relação entre o momentum total e a
densidade de elétrons (1.12), demonstramos
que a pressão de elétrons é determinada pela
densidade de elétrons:
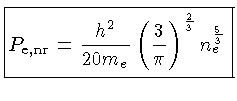 |
(1.14) |
Podemos expressar a densidade de elétrons em termos da
densidade de massa [veja eq. (1.61)]
onde
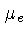 aqui é o peso molecular médio por elétron,
ou seja, o número médio de massas atômicas (A) por elétron:
e
onde
aqui é o peso molecular médio por elétron,
ou seja, o número médio de massas atômicas (A) por elétron:
e
onde 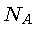 é o número de Avogadro [Amedeo Avogadro (1776-1856)].
Normalmente
é o número de Avogadro [Amedeo Avogadro (1776-1856)].
Normalmente
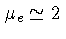 , a não ser que o gás contenha uma fração
substancial de hidrogênio, o que não é geralmente o caso
pois o estado degenerado é atingido no núcleo de estrelas
que já queimaram o hidrogênio,
e os núcleos de anãs brancas são predominantemente
compostos de He, C, O, ou Ne, todos com A/Z=2.
Mas para os interiores de planetas gigantes e anãs marrons,
onde também há degenerescência, o hidrogênio
é dominante.
, a não ser que o gás contenha uma fração
substancial de hidrogênio, o que não é geralmente o caso
pois o estado degenerado é atingido no núcleo de estrelas
que já queimaram o hidrogênio,
e os núcleos de anãs brancas são predominantemente
compostos de He, C, O, ou Ne, todos com A/Z=2.
Mas para os interiores de planetas gigantes e anãs marrons,
onde também há degenerescência, o hidrogênio
é dominante.
Note que a pressão degenerada e não
relativística dada pela equação
(1.15) não depende da temperatura
e, portanto, um aumento da temperatura não causa um aumento da pressão,
e subsequente expansão, que reduziria a temperatura. Este fato
tem implicações na história evolutiva das estrelas,
desde a queima explosiva do hélio até a explosão de
supernova, como veremos no decorrer deste capítulo.
Vemos pela equação
(1.15) que a pressão de um gás de elétrons
degenerado aumenta como uma potência 5/3 da densidade.
Como para um gás não degenerado a pressão aumenta linearmente
com a densidade, é claro que, com o aumento de densidade,
existe um ponto em que a pressão degenerada será maior
do que o valor dado pela fórmula não degenerada.
Podemos definir uma linha no plano 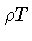 dividindo a
região degenerada da não-degenerada, calculando-se
os valores para os quais as duas fórmulas são iguais:
dividindo a
região degenerada da não-degenerada, calculando-se
os valores para os quais as duas fórmulas são iguais:
ou seja, a pressão completamente degenerada supera a pressão
não-degenerada para densidades maiores do que
Naturalmente a transição de não-degenerado para degenerado não
ocorre abruptamente, mas sim suavemente. Na região de
transição, precisamos utilizar a equação que discutiremos
na
seção de degenerescência parcial. Para o interior do Sol, onde
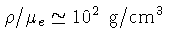 e
e
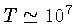 K,
a inequalidade mostra que o gás está completamente não-degenerado.
Para o interior de uma anã-branca, onde
K,
a inequalidade mostra que o gás está completamente não-degenerado.
Para o interior de uma anã-branca, onde
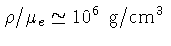 e
e
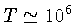 K,
a inequalidade se satisfaz, e a pressão degenerada domina.
K,
a inequalidade se satisfaz, e a pressão degenerada domina.





Próxima: Degenerescência Total Relativística
Volta: Degenerescência dos Elétrons
Anterior: Degenerescência Total
©
Modificada em 22 nov 2004
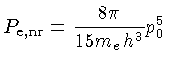
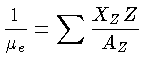
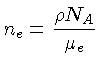
![]() dividindo a
região degenerada da não-degenerada, calculando-se
os valores para os quais as duas fórmulas são iguais:
dividindo a
região degenerada da não-degenerada, calculando-se
os valores para os quais as duas fórmulas são iguais: