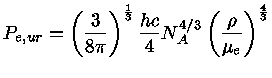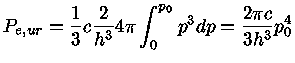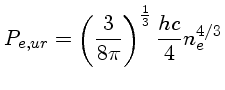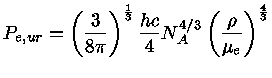Próxima: Degenerescência Parcial
Volta: Degenerescência dos Elétrons
Anterior: Degenerescência Total Não-Relativística
Conforme a densidade de elétrons aumenta, o momentum máximo
de um gás de elétrons completamente degenerado aumenta. Em uma
certa densidade,
os elétrons mais energéticos se tornarão relativísticos.
Nestas condições, a substituição de 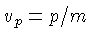 utilizada
para derivar a equação (1.13) é incorreta,
e precisamos utilizar a expressão da relatividade
ou seja
Podemos estimar a densidade para a qual os elétrons tornam-se
relativísticos, calculando-se
utilizada
para derivar a equação (1.13) é incorreta,
e precisamos utilizar a expressão da relatividade
ou seja
Podemos estimar a densidade para a qual os elétrons tornam-se
relativísticos, calculando-se
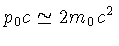 .
Usando-se o momentum máximo derivado na equação
(1.12), obtemos
.
Usando-se o momentum máximo derivado na equação
(1.12), obtemos
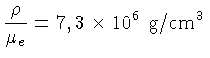
relativístico
Ou seja, para densidades aproximando-se deste valor precisamos usar
a cinemática relativística.
Inserindo-se a velocidade relativística na integral da
pressão (1.7), obtemos
Para calcular esta integral podemos definir um novo parâmetro
de modo que
e a integral pode ser escrita como
que pode ser integrada, resultando em
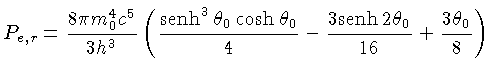 |
(1.16) |
e, em termos do momentum de Fermi,
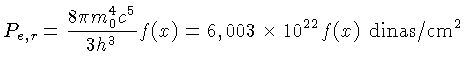 |
(1.17) |
onde
Degenerescência total ultra-relativística
No limite ultra-relativístico, 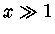 ,
,
e usando-se somente o primeiro termo da expansão:
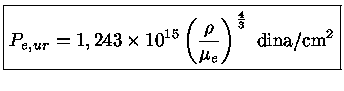 |
(1.17a) |
Uma derivação mais simples do limite ultra-relativístico
pode ser obtido da definição de pressão (1.7),
utilizando (1.10a),
assumindo
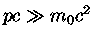 e portanto
e portanto
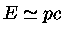 ;
como
;
como
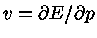 ,
, 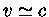 :
Utilizando a relação entre o momentum de Fermi
:
Utilizando a relação entre o momentum de Fermi
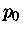 e a densidade dada pela equação (1.12):
ou, termos da densidade de massa, recuperamos a equação para
Pe,ur
Portanto a pressão degenerada ultra-relativística
depende da potência 4/3 da densidade e, novamente, não
depende da temperatura.
e a densidade dada pela equação (1.12):
ou, termos da densidade de massa, recuperamos a equação para
Pe,ur
Portanto a pressão degenerada ultra-relativística
depende da potência 4/3 da densidade e, novamente, não
depende da temperatura.





Próxima: Degenerescência Parcial
Volta: Degenerescência dos Elétrons
Anterior: Degenerescência Total Não-Relativística
©
Modificada em 18 abril 2006
![$p=\frac{m_0v}{[1-(v/c)^2]^\frac{1}{2}}$](img117.gif)
![$p=\frac{m_0v}{[1-(v/c)^2]^\frac{1}{2}}$](img117.gif)
![$v=\frac{p/m_0}{[1-(p/m_0c)^2]^\frac{1}{2}}$](img118.gif)
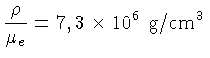 relativístico
relativístico
![$P_{e,r} = \frac{8\pi}{3mh^3}\int_0^{p_0} \frac{p^4dp}{[1+(p/m_0c)^2]^\frac{1}{2}}$](img121.gif)
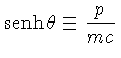
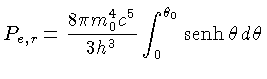
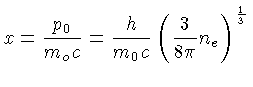
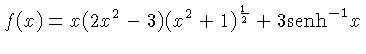
![]() ,
,