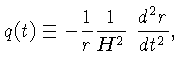 |
(1.20) |
Usando as equações (4), (8) e (10) obtemos:
Logo, o valor de ![]() , assim como o de
, assim como o de ![]() determinam o futuro
da expansão do Universo.
Note que
determinam o futuro
da expansão do Universo.
Note que ![]() ,
, ![]() e
e ![]() são funções do
tempo.
Mas o fato de
são funções do
tempo.
Mas o fato de
![]() ser constante, juntamente com as equações
(11) e (21), garante
que se
ser constante, juntamente com as equações
(11) e (21), garante
que se
![]() (ou analogamente
(ou analogamente
![]() ) em um dado instante,
esta condição continua satisfeita ao longo do tempo, ainda que o
valor do parâmetro varie.
A determinação do parâmetro de densidade (ou do parâmetro
de desaceleração) do Universo em seu estágio atual contém
informação
sobre o desenlace da competição entre a
expansão do Universo e a gravitação
que tende a contê-la.
) em um dado instante,
esta condição continua satisfeita ao longo do tempo, ainda que o
valor do parâmetro varie.
A determinação do parâmetro de densidade (ou do parâmetro
de desaceleração) do Universo em seu estágio atual contém
informação
sobre o desenlace da competição entre a
expansão do Universo e a gravitação
que tende a contê-la.