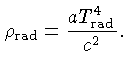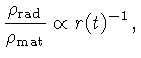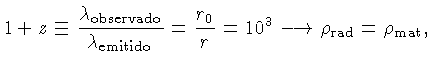

Próxima: Cosmologia Relativística
Volta: Cosmologia Newtoniana
Anterior: Parâmetro de Desaceleração
Levando-se em conta que a densidade de energia
de um campo de radiação é dada por:
a densidade de massa equivalente (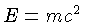 ) é dada por:
Para comparação, se assumirmos
) é dada por:
Para comparação, se assumirmos
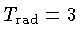 K,
obtemos
K,
obtemos
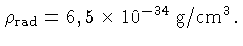 Usando-se a lei de Wien [Wilhelm Wien (1864-1928)],
e usando-se a relação de desvio para o vermelho devido à expansão
do Universo:
onde
Usando-se a lei de Wien [Wilhelm Wien (1864-1928)],
e usando-se a relação de desvio para o vermelho devido à expansão
do Universo:
onde 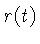 é a escala do Universo, representada pela
distância média entre as galáxias, obtemos:
ou seja, a densidade de radiação
enquanto que a densidade de matéria é inversamente proporcional
ao volume do Universo:
Deste modo obtemos que
indicando que quando o Universo era muito mais jovem, para
isto é, quando o Universo era muito jovem (
é a escala do Universo, representada pela
distância média entre as galáxias, obtemos:
ou seja, a densidade de radiação
enquanto que a densidade de matéria é inversamente proporcional
ao volume do Universo:
Deste modo obtemos que
indicando que quando o Universo era muito mais jovem, para
isto é, quando o Universo era muito jovem (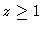 ) ele era dominado pela
radiação. Nesta definição,
) ele era dominado pela
radiação. Nesta definição, 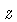 é chamado de deslocamento
para o vermelho, redshift, devido ao efeito Doppler.
é chamado de deslocamento
para o vermelho, redshift, devido ao efeito Doppler.


Próxima: Cosmologia Relativística
Volta: Cosmologia Newtoniana
Anterior: Parâmetro de Desaceleração
©
Modificada em 1999-02-06