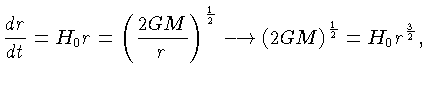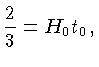

Próxima: Parâmetro de Densidade
Volta: Cosmologia Newtoniana
Anterior: Densidade Crítica
Idade do Universo
Como a lei de Hubble, que
relaciona a velocidade de expansão da galáxia, v,
com a distância a esta, d, é dada por
assumindo que a velocidade v permaneceu constante no tempo,
isto é, que não houve desaceleração,
ou seja que o Universo é aberto.
Podemos também derivar a idade do Universo para o caso do
Universo plano (E=0), escrevendo 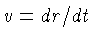 na equação da
energia total:
na equação da
energia total:
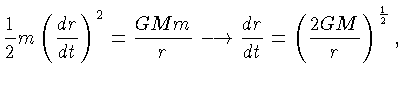 |
(1.4) |
ou
Integrando-se os dois lados, e usando r=0 para t=0, obtemos:
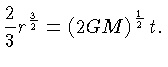 |
(1.5) |
Como a lei de Hubble pode ser escrita como:
podemos usar a equação (4) para escrever o termo
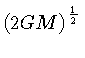 em função da constante de
Hubble:
que substituindo na equação (5) nos dá:
em função da constante de
Hubble:
que substituindo na equação (5) nos dá:
Lembre-se que 1 Mpc corresponde a 3,26 milhões de anos-luz e
que a dimensão da constante de Hubble H é
simplesmente o inverso de tempo. As unidades que usamos simplesmente
explicitam que quando olhamos a um Mpc, a velocidade é
de recessão das galáxias é da ordem de
50 a 100 km/s.

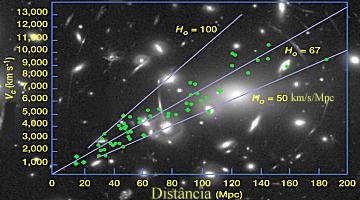
A constante de Hubble é derivada medindo-se independentemente
da velocidade, a distância às galáxias, como
usando o fato de que as estrelas Cefeidas são intrinsicamente
mais brilhantes quanto maior é o período de pulsação.
Calculador
para a idade do Universo:
Para Ho = 71 km/s/Mpc, ΩM=0,270, Ωvac=0,730,
z=11 corresponde à idade de 462 milhões de anos, e o Universo tem agora
13,665 bilhões de anos. Este é o z compatível com as observações do WMAP
para a época da formação das primeiras estrelas, isto é, da reionização
do Universo.


Próxima: Parâmetro de Densidade
Volta: Cosmologia Newtoniana
Anterior: Densidade Crítica
©
Modificada em 21 abril 2007
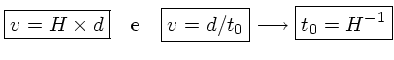
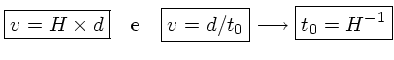
![]() na equação da
energia total:
na equação da
energia total:
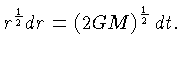
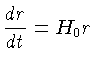
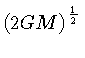 em função da constante de
Hubble:
em função da constante de
Hubble: