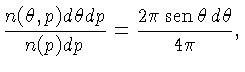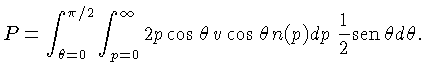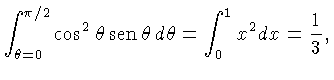Próxima: Gás Não Degenerado
Volta: Interiores Estelares
Anterior: Temperatura
Um gás perfeito (ideal)
é definido como aquele em que não há interação
entre as partículas do gás. Embora este critério nunca seja satisfeito,
a aproximação é válida quando a energia de interação entre
as partículas é muito menor que sua energia térmica.
A fonte microscópica de pressão em um gás perfeito é
o bombardeamento de partículas. A reflexão, ou absorção,
destas partículas em uma superfície real ou imaginária
resulta em transferência de momentum para esta superfície.
Pela Segunda Lei de Newton (F=dp/dt),
o momentum transferido
exerce uma força na superfície. A força média
por unidade de área é chamada de pressão.
É a mesma quantidade na expressão: trabalho =
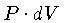 , em
uma expansão infinitesimal.
, em
uma expansão infinitesimal.
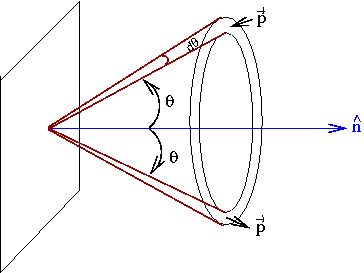
Pressão: Secção cônica na direção θ
à normal.
Para um gás em equilíbrio térmico, a
distribuição de momentum é
isotrópica, isto é, as partículas se movem com a mesma probabilidade
em todas as direções. Quando refletidas em uma superfície,
as partículas transferem momentum a esta superfície.
Quando uma partícula de momentum p,
deslocando-se com um ângulo θ
à normal,
é refletida na superfície,
o momentum transferido é
Seja
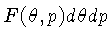 é o número de partículas
com momentum p
no intervalo dp
colidindo com a parede,
por unidade de área, por unidade de tempo, de todas as
direções inclinadas com um ângulo θ
à normal,
no intervalo dθ.
A contribuição à
pressão total (dP)
é dada por:
de modo que a pressão total
é o número de partículas
com momentum p
no intervalo dp
colidindo com a parede,
por unidade de área, por unidade de tempo, de todas as
direções inclinadas com um ângulo θ
à normal,
no intervalo dθ.
A contribuição à
pressão total (dP)
é dada por:
de modo que a pressão total 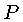 é:
é:
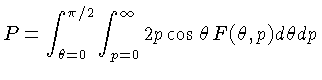 |
(1.6) |
O fluxo de partículas
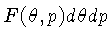 de velocidade v pode ser calculado
como o produto da densidade de partículas com momentum p
movendo-se no cone com ângulo θ,
vezes o volume das partículas
que passarão pela unidade de área, na unidade de tempo.
Este volume é dado por:
de velocidade v pode ser calculado
como o produto da densidade de partículas com momentum p
movendo-se no cone com ângulo θ,
vezes o volume das partículas
que passarão pela unidade de área, na unidade de tempo.
Este volume é dado por:
para dA e dt unitários já que estamos calculando
o fluxo, isto é, número de partículas por unidade de área e unidade de tempo. Logo,
onde
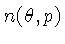 é a densidade (número de partículas
por unidade de volume) no cone referido.
é a densidade (número de partículas
por unidade de volume) no cone referido.
Para um gás isotrópico:
que é a fração do ângulo esférico total definido pelo cone.
Ou seja, a pressão é dada por:
Como
a pressão de um gás isotrópico é dada por:
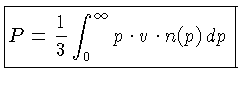 |
(1.7) |
Esta integral precisa ser calculada para diferentes circunstâncias,
já que a relação entre o momentum
p
e a velocidade v
depende de considerações
relativísticas, enquanto a forma da distribuição
n(p)
depende do tipo de partículas e da estatística
quântica.





Próxima: Gás Não Degenerado
Volta: Interiores Estelares
Anterior: Temperatura
 Astronomia e Astrofísica
Astronomia e Astrofísica
 ©
©
Modificada em 8 ago 2011
![]() , em
uma expansão infinitesimal.
, em
uma expansão infinitesimal.
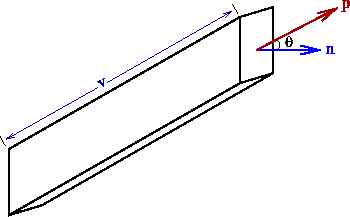
![]() de velocidade v pode ser calculado
como o produto da densidade de partículas com momentum p
movendo-se no cone com ângulo θ,
vezes o volume das partículas
que passarão pela unidade de área, na unidade de tempo.
Este volume é dado por:
de velocidade v pode ser calculado
como o produto da densidade de partículas com momentum p
movendo-se no cone com ângulo θ,
vezes o volume das partículas
que passarão pela unidade de área, na unidade de tempo.
Este volume é dado por: