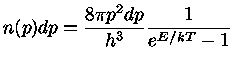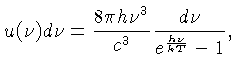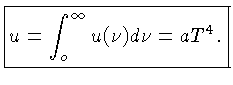Próxima: Degenerescência dos Elétrons
Volta: Pressão Mecânica
Anterior: Gás Não Degenerado
Para um gás de fótons,
como cada fóton tem um momentum associado
eles também exercem uma pressão, chamada
pressão de radiação
 :
onde
:
onde 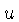 é a densidade de energia (energia
por unidade de volume) da radiação:
onde
é a densidade de energia (energia
por unidade de volume) da radiação:
onde 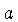 é a constante de Stefan-Boltzmann:
é a constante de Stefan-Boltzmann:
O valor da densidade de energia 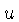 vem do fato que
a energia de cada fóton é dada por
vem do fato que
a energia de cada fóton é dada por 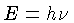 ,
e o momentum
,
e o momentum 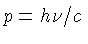 , de modo que, usando a
distribuição de momentum de Bose-Einstein
com
, de modo que, usando a
distribuição de momentum de Bose-Einstein
com 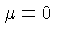 ,
,
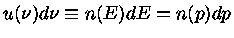 , e
, e
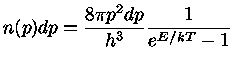
|
(1.7a) |
obtém-se que a densidade de energia
de fótons com uma frequência 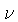 no intervalo
no intervalo
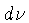 , em equilíbrio térmico é dada por:
de modo que
, em equilíbrio térmico é dada por:
de modo que
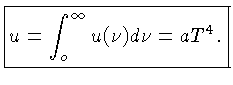
|
(1.7b) |
Existem casos, como em estrelas quentes de população I e II,
que a pressão de
radiação é comparável com a pressão do gás,
que sustenta a estrela. De fato, para estrelas destas populações
com massa
maior que 100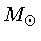 , a pressão de radiação,
principalmente nos grãos formados em suas camadas mais externas,
é maior do que a força gravitacional por
unidade de área, e a pressão de radiação
causa a ejeção das camadas externas da estrela.
, a pressão de radiação,
principalmente nos grãos formados em suas camadas mais externas,
é maior do que a força gravitacional por
unidade de área, e a pressão de radiação
causa a ejeção das camadas externas da estrela.





Próxima: Degenerescência dos Elétrons
Volta: Pressão Mecânica
Anterior: Gás Não Degenerado
©
Modificada em 15 mar 2006
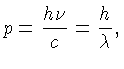
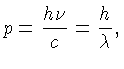
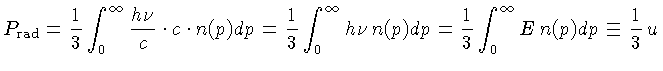
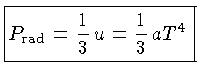
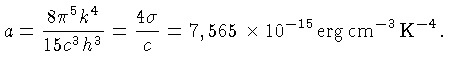
![]() vem do fato que
a energia de cada fóton é dada por
vem do fato que
a energia de cada fóton é dada por ![]() ,
e o momentum
,
e o momentum ![]() , de modo que, usando a
distribuição de momentum de Bose-Einstein
com
, de modo que, usando a
distribuição de momentum de Bose-Einstein
com ![]() ,
,
![]() , e
, e