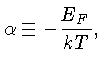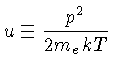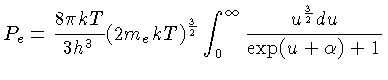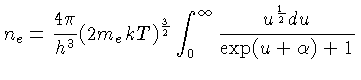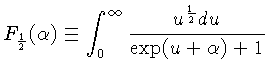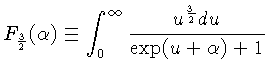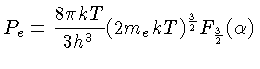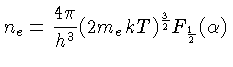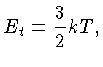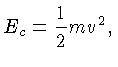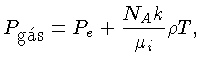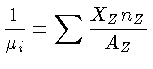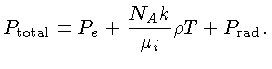Próxima: Equilíbrio Hidrostático
Volta: Pressão Mecânica
Anterior: Degenerescência Total Relativística
Para a região de transição, ou para o caso geral, precisamos
utilizar a distribuição de Fermi-Dirac na equação da
pressão (1.7):
![$P_e = \frac{8\pi}{3h^3}\int_0^\infty \frac{p^3v_pdp}{\exp[(E-E_F)/kT]+1}$](img129.gif) |
(1.18) |
e obter a energia de Fermi 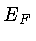 integrando-se a densidade total:
integrando-se a densidade total:
![$n_e = \frac{2}{h^3}\int_0^\infty \frac{4\pi p^2dp}{\exp[(E-E_F)/kT]+1}$](img130.gif) |
(1.19) |
Para temperaturas menores que 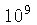 K, a degenerescência total
inicia-se antes dos elétrons tornarem-se
relativísticos, de modo que podemos nos restringir a
velocidades não relativísticas para a degenerescência parcial,
isto é, podemos utilizar
K, a degenerescência total
inicia-se antes dos elétrons tornarem-se
relativísticos, de modo que podemos nos restringir a
velocidades não relativísticas para a degenerescência parcial,
isto é, podemos utilizar 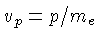 , de modo que
, de modo que
![$P_e = \frac{8\pi}{3h^3m_e}\int_0^\infty \frac{p^4dp}{\exp[(\frac{p^2}{2m_e}-E_F)/kT]+1}$](img133.gif) |
(1.20) |
e
![$n_e = \frac{8\pi}{h^3}\int_0^\infty \frac{p^2dp}{\exp[(\frac{p^2}{2m_e}-E_F)/kT]+1}$](img134.gif) |
(1.21) |
Podemos definir dois parâmetros adimensionais, a energia
de Fermi comparada com a energia térmica,
e a energia cinética comparada com a energia térmica,
e escrever
e
constituindo duas equações paramétricas para a
equação de estado.
Definindo-se duas funções:
que não têm solução exatas, podemos escrever
e
e finalmente
![${P_e = n_e kT \left[\frac{2F_\frac{3}{2}(\alpha)}{3F_\frac{1}{2}(\alpha)}\right]}$](img143.gif) |
(1.22) |
O fator
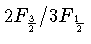 mede o desvio da pressão
eletrônica em relação ao gás não degenerado, e
varia de 8 para
mede o desvio da pressão
eletrônica em relação ao gás não degenerado, e
varia de 8 para
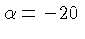 (energia térmica muito maior
do que a energia de Fermi), a 1 para
(energia térmica muito maior
do que a energia de Fermi), a 1 para 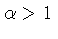 (energia de Fermi maior do que a energia térmica).
(energia de Fermi maior do que a energia térmica).
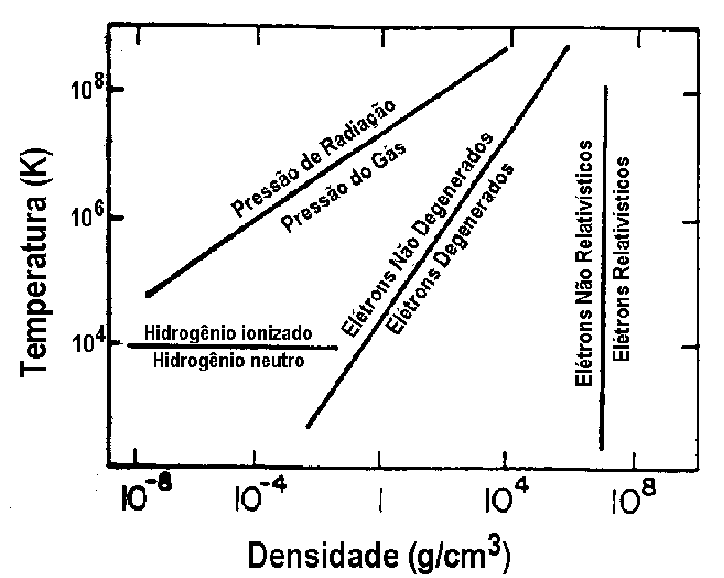 Diagrama mostrando qual o estado do gás para as combinações
de densidade e temperatura (
Diagrama mostrando qual o estado do gás para as combinações
de densidade e temperatura (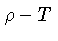 ).
).
Note que os íons normalmente são não degenerados,
exceto nas estrelas de nêutrons,
pois
seu espaço de fase é muito maior que o dos elétrons já
que sua massa é cerca de 2000 vezes maior;
para a mesma energia térmica
que corresponde a energia cinética,
pois os íons são
não relativísticos,
a velocidade dos íons é muito menor do que a velocidade dos
elétrons.
Portanto:
onde 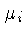 é o peso molecular médio dos íons
Precisamos ainda levar em conta a contribuição
da pressão de radiação à pressão total.
Para comparação, esta contribuição passa de 2,1%
para uma estrela de 5
é o peso molecular médio dos íons
Precisamos ainda levar em conta a contribuição
da pressão de radiação à pressão total.
Para comparação, esta contribuição passa de 2,1%
para uma estrela de 5 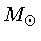 para 11% para uma estrela de 15
para 11% para uma estrela de 15 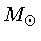 .
.





Próxima: Equilíbrio Hidrostático
Volta: Pressão Mecânica
Anterior: Degenerescência Total Relativística
©
Modificada em 15 mar 2006
![$P_e = \frac{8\pi}{3h^3}\int_0^\infty \frac{p^3v_pdp}{\exp[(E-E_F)/kT]+1}$](img129.gif)