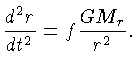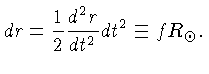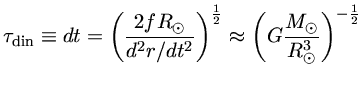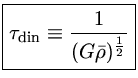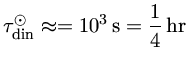Próxima: Reserva de Energia de uma Estrela
Volta: Interiores Estelares
Anterior: Degenerescência Parcial
Mesmo para a estrela mais bem estudada só podemos medir 4 parâmetros:
massa, luminosidade, raio e composição química das camadas
externas. Podemos determinar a estrutura da estrela com estes parâmetros,
porque dispomos de mais uma condição: a constância das
estrelas por longos períodos de tempo. Mesmo as estrelas variáveis
apresentam estabilidade da estrutura média por longos tempos.
A existência de algas fósseis na Terra com mais de 1 bilhão
de anos e fósseis de até 3,5 bilhões de anos,
são evidência de que a temperatura
da Terra não pode ter mudado mais que aproximadamente 20°C.
Portanto, o interior das estrelas precisa estar em perfeito
equilíbrio.
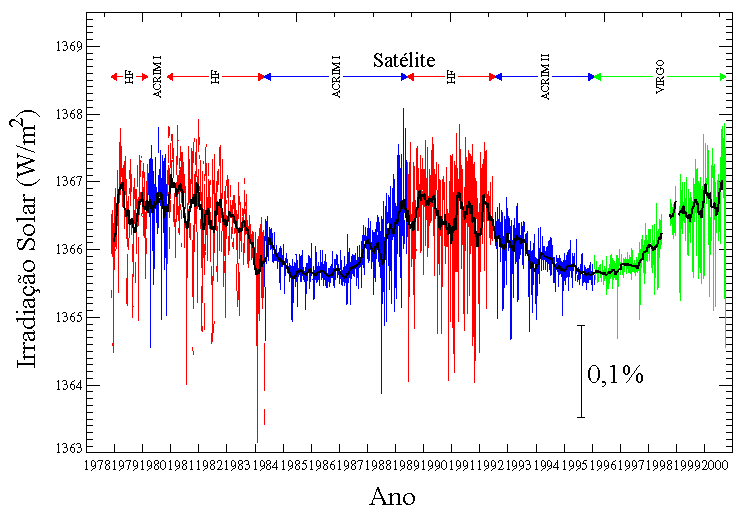 Irradiação solar (constante solar) medida nos
últimos anos através de satélites.
Irradiação solar (constante solar) medida nos
últimos anos através de satélites.
Construiremos um conjunto de condições que precisam ser
cumpridas em todas as camadas das estrelas. Ignoraremos
perturbações como rotação, pulsação,
distorção por forças de maré e campos magnéticos
de larga escala. Consequentemente, podemos assumir
simetria esférica.
A primeira condição que precisa ser cumprida pelo interior
estelar é a condição de equilíbrio hidrostático
(mecânico):
todas as forças atuando em qualquer elemento de volume
dentro da estrela têm que ser compensadas exatamente,
já que uma força resultante não nula implicaria
movimentos e, portanto, mudanças na estrutura. As únicas
forças que precisamos considerar são a
força gravitacional,
para dentro, e a força de pressão, para fora.
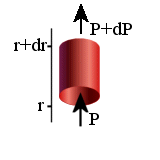 Vamos considerar um elemento de volume cilíndrico,
a uma distância r
do centro da estrela, com seu eixo
na direção do centro, com uma seção transversal
ds
e um comprimento dr.
A força de pressão atuando sobre
este elemento, isto é,
a diferença entre a força de pressão na parede interna
e a força de pressão na parede externa, é dada por:
Vamos considerar um elemento de volume cilíndrico,
a uma distância r
do centro da estrela, com seu eixo
na direção do centro, com uma seção transversal
ds
e um comprimento dr.
A força de pressão atuando sobre
este elemento, isto é,
a diferença entre a força de pressão na parede interna
e a força de pressão na parede externa, é dada por:
onde P
é a pressão, que será uma função,
monotonicamente decrescente, da distância r
ao centro.
A força gravitacional atuando sobre o mesmo volume
será dada pela massa do volume, vezes a aceleração
gravitacional, isto é:
onde 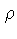 é a densidade e G
é a constante gravitacional.
Expressamos a aceleração gravitacional em termos de Mr,
que significa a massa em uma esfera de raio r
e pode ser expressa em termos da densidade como:
é a densidade e G
é a constante gravitacional.
Expressamos a aceleração gravitacional em termos de Mr,
que significa a massa em uma esfera de raio r
e pode ser expressa em termos da densidade como:
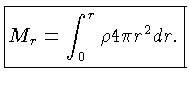 |
(1.23) |
Esta equação é chamada de equação da massa, ou
equação da continuidade.
Lembramos que a força exercida pelas camadas externas
é nula.
Igualando as duas forças opostas, obtemos a
condição de equilíbrio hidrostático:
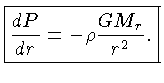 |
(1.24) |
Ou caso não haja simetria esférica
onde 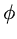 é o potencial gravitacional.
é o potencial gravitacional.
Se a pressão de radiação for importante, esta equação
precisa incluir o momentum transferido pelo campo de radiação
à matéria
onde κ é o coeficiente de absorção,
que descreve a
probabilidade de que um fóton será ou absorvido ou espalhado,
e F é o fluxo de energia transportado por radiação por unidade
de área. Mas este termo pode ser simplesmente incluído
na pressão total.
Em unidades do sistema c.g.s., a gravidade de uma estrela de massa M em um ponto r é
dada por:
As equações (1.23) e (1.24) são as duas
primeiras das equações que governam a estrutura estelar.
Sozinhas elas são claramente insuficientes para determinar
com unicidade como a pressão, densidade e massa variam
com a distância ao centro da estrela.
Mas elas permitem obter uma estimativa da ordem de grandeza
da pressão e temperatura que vamos encontrar. Vamos aplicar
a equação de equilíbrio hidrostático (1.24)
para um ponto no meio do Sol. Podemos usar, para
uma primeira estimativa, a densidade média do Sol
para
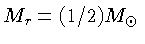 , a metade da massa do Sol,
, a metade da massa do Sol,
 ,
e para
,
e para
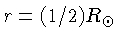 a metade do raio do Sol,
a metade do raio do Sol,
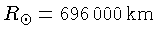 .
Além disto, para o lado esquerdo da equação (1.24),
podemos usar
.
Além disto, para o lado esquerdo da equação (1.24),
podemos usar
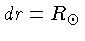 , para
, para
 ,
e assumirmos
,
e assumirmos
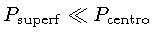 .
Usando G=6,67 × 108 dina cm-2 g-2,
obtemos:
usando unidades c.g.s (cm grama seg). Como 1 N/m2=10 dina/cm2,
PcentroSol=5,3 × 1014 N/m2,
no sistema mks (metro kg seg).
.
Usando G=6,67 × 108 dina cm-2 g-2,
obtemos:
usando unidades c.g.s (cm grama seg). Como 1 N/m2=10 dina/cm2,
PcentroSol=5,3 × 1014 N/m2,
no sistema mks (metro kg seg).
Desta estimativa de pressão, podemos imediatamente estimar a temperatura,
se usarmos a equação de estado de um gás ideal, que,
como demonstraremos depois, é valida para a maioria das
estrelas. A equação do gás ideal pode ser escrita como
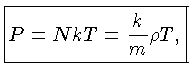 |
(1.25) |
onde 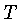 é a temperatura,
é a temperatura, 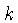 a constante de Boltzmann, e
a constante de Boltzmann, e 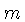 o peso molecular médio, já que
o peso molecular médio, já que 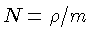 . Para
. Para 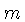 podemos
usar a metade da massa do próton, já que o hidrogênio
é o elemento mais abundante, e para hidrogênio ionizado,
um próton e um elétron atuam como duas partículas
com massa média de meia massa do próton já que
podemos
usar a metade da massa do próton, já que o hidrogênio
é o elemento mais abundante, e para hidrogênio ionizado,
um próton e um elétron atuam como duas partículas
com massa média de meia massa do próton já que
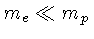 .
.
Para o caso geral,
isto é, precisamos levar em conta a pressão do gás
e a pressão de radiação,
mas no interior de estrelas de baixa massa, como o Sol,
e podemos desprezá-la.
Aplicando para a pressão central do Sol, ainda usando a
densidade média do Sol, obtemos:
Isto é, encontramos uma temperatura típica no
interior do Sol de 10 milhões de graus Kelvin.
Podemos agora estimar a pressão de radiação
Prad=(1/3)aT4 = 2,5 × 10-15 erg cm-3K-4× 1028K4=2,5 × 1013 dina/cm2
ou seja, Pgás > 100 Prad para o Sol.
Com estas estimativas podemos ver o cenário que temos que trabalhar.
A esta temperatura, o
máximo da função de Planck
está em 2,9 Å, muito mais energético do
que os 912 Å
de comprimento de onda mínimo para a ionização do hidrogênio.
Os gases estão muito quentes para conter qualquer composto
químico, e quentes o suficiente para estarem altamente
ionizados. Não precisamos portanto considerar a
física complexa de sólidos e líquidos.
O hidrogênio e o hélio, principais constituintes,
estão completamente ionizados, e aparecerão como prótons,
elétrons, e partículas 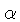 .
.
Antes de assumir
estrita obediência ao equilíbrio
hidrostático, vamos estimar qual é o custo da
não obediência. Vamos assumir que em algum lugar
da estrela a aceleração gravitacional não
é estritamente balançada pela força
de pressão, deixando uma fração 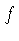 não
balançada. O material então será
acelerado por uma quantia:
não
balançada. O material então será
acelerado por uma quantia:
Podemos resolver esta equação para o valor de 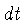 em que a aceleração não balançada causa um deslocamento
em que a aceleração não balançada causa um deslocamento
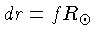 .
Assumindo um movimento retilíneo uniformemente acelerado,
Logo, para o ponto no meio do Sol:
Isto é, qualquer desequilíbrio da condição
de equilíbrio hidrostático causa deslocamentos grandes e
rápidos. Este tempo é chamado de tempo
de queda livre, ou tempo dinâmico.
Portanto, uma falta de equilíbrio leva a mudanças
significativas no raio da estrela. Como o raio do Sol não
mudou significativamente durante bilhões de anos,
ou a temperatura na Terra teria variado,
a equação de equilíbrio hidrostático é
satisfeita com alta precisão.
.
Assumindo um movimento retilíneo uniformemente acelerado,
Logo, para o ponto no meio do Sol:
Isto é, qualquer desequilíbrio da condição
de equilíbrio hidrostático causa deslocamentos grandes e
rápidos. Este tempo é chamado de tempo
de queda livre, ou tempo dinâmico.
Portanto, uma falta de equilíbrio leva a mudanças
significativas no raio da estrela. Como o raio do Sol não
mudou significativamente durante bilhões de anos,
ou a temperatura na Terra teria variado,
a equação de equilíbrio hidrostático é
satisfeita com alta precisão.





Próxima: Reserva de Energia de uma Estrela
Volta: Interiores Estelares
Anterior: Degenerescência Parcial
©
Modificada em 30 set 2008


 Vamos considerar um elemento de volume cilíndrico,
a uma distância r
do centro da estrela, com seu eixo
na direção do centro, com uma seção transversal
ds
e um comprimento dr.
A força de pressão atuando sobre
este elemento, isto é,
a diferença entre a força de pressão na parede interna
e a força de pressão na parede externa, é dada por:
Vamos considerar um elemento de volume cilíndrico,
a uma distância r
do centro da estrela, com seu eixo
na direção do centro, com uma seção transversal
ds
e um comprimento dr.
A força de pressão atuando sobre
este elemento, isto é,
a diferença entre a força de pressão na parede interna
e a força de pressão na parede externa, é dada por:
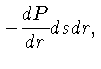
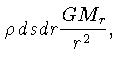
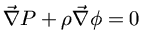
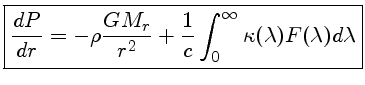
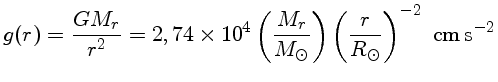
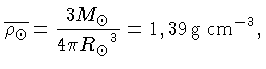
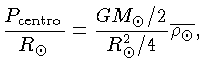
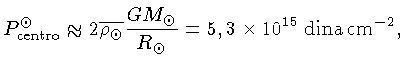
![]() .
.
![]() não
balançada. O material então será
acelerado por uma quantia:
não
balançada. O material então será
acelerado por uma quantia: