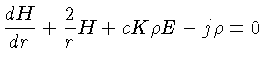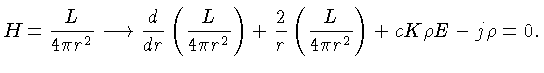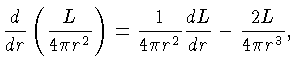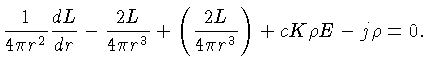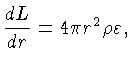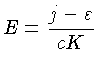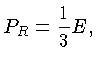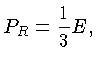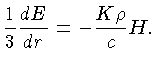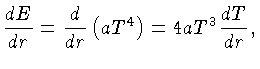Próxima: Ordem de Grandeza da Luminosidade
Volta: Interiores Estelares
Anterior: A Equação de Transporte Radiativo
A solução da equação (1.36) para o campo de
radiação representa um dos principais problemas na
teoria de atmosferas estelares. Para o interior estelar,
o problema é simplificado pelo fato do campo ser
quase isotrópico. Ao invés de trabalharmos com
a intensidade 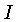 , que representa a distribuição
de radiação para cada direção, vamos considerar
os três primeiros momentos da distribuição,
a densidade de energia
, que representa a distribuição
de radiação para cada direção, vamos considerar
os três primeiros momentos da distribuição,
a densidade de energia
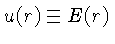 , o fluxo da radiação
-->
, o fluxo da radiação
-->
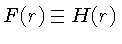 , e a pressão de radiação
, e a pressão de radiação 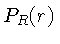 .
.
Por definição, a intensidade é a energia que atravessa
a superfície, na direção 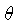 , por unidade de área,
por unidade de tempo, por unidade de ângulo sólido. O
fluxo é a energia, por unidade de área,
por unidade de tempo,
em todas as direções:
, por unidade de área,
por unidade de tempo, por unidade de ângulo sólido. O
fluxo é a energia, por unidade de área,
por unidade de tempo,
em todas as direções:
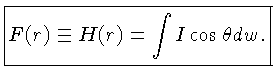 |
(1.37) |
A densidade de energia, ou energia por unidade de volume, pode ser derivada
notando-se que, se F for a quantidade de energia cruzando a
área 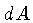 , em uma direção
, em uma direção 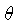 , por unidade de tempo,
em um segundo, a radiação F ocupará um volume
, por unidade de tempo,
em um segundo, a radiação F ocupará um volume
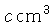 .
Então, a energia por unidade de volume, será dada por:
.
Então, a energia por unidade de volume, será dada por:
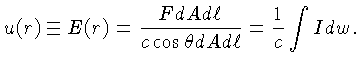 |
(1.38) |
Sabemos que a energia cruzando a área 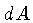 é
é
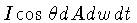 .
O número de fótons é dado pela energia
total dividida pela energia de cada fóton,
.
O número de fótons é dado pela energia
total dividida pela energia de cada fóton, 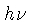 . Como o momentum
de cada fóton é dado por
. Como o momentum
de cada fóton é dado por 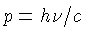 , a pressão
transferida para a área normal a direção
, a pressão
transferida para a área normal a direção
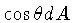 ,
será dada por
,
será dada por
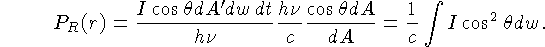 |
(1.39) |
para dA' e dt unitários.
Integrando (1.36) sobre o elemento de ângulo sólido 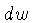 , obtemos:
, obtemos:
Usando-se a definição (1.37) e (1.38), e notando que o
segundo termo pode ser escrito como:
obtemos:
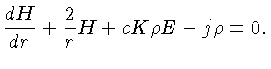 |
(1.40) |
Outra relação é obtida
multiplicando-se (1.36) por
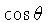 e integrando sobre
e integrando sobre 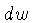 :
A integral no primeiro termo é igual a
:
A integral no primeiro termo é igual a 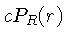 , e a do
terceiro termo é igual a
, e a do
terceiro termo é igual a 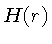 .
O último termo é nulo pois,
.
O último termo é nulo pois,
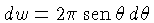 , e:
No segundo termo, fazendo-se uma integração por partes,
com
, e:
No segundo termo, fazendo-se uma integração por partes,
com
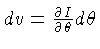 e
e
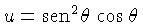 :
:
Logo:
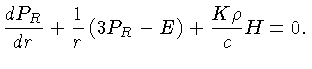 |
(1.41) |
Obtivemos somente duas equações com três funções,
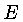 ,
, 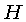 e
e 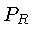 . Esta insuficiência quase sempre é
encontrada quando se substitui uma equação diferencial
parcial, como a equação (1.36), por um conjunto
de equações diferenciais ordinárias, com as
equações (1.40) e (1.41). Para resolver
o sistema, encontraremos uma relação adicional
entre os momentos, usando a quase isotropia do campo
de radiação no interior estelar.
. Esta insuficiência quase sempre é
encontrada quando se substitui uma equação diferencial
parcial, como a equação (1.36), por um conjunto
de equações diferenciais ordinárias, com as
equações (1.40) e (1.41). Para resolver
o sistema, encontraremos uma relação adicional
entre os momentos, usando a quase isotropia do campo
de radiação no interior estelar.
Representemos o campo de radiação em qualquer ponto
da estrela por uma série:
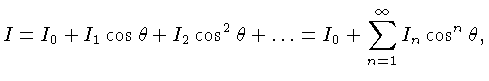 |
(1.42) |
e determinemos a taxa de convergência desta série introduzindo-a
na equação de equilíbrio radiativo (1.36):
Como nossa expansão vale para qualquer 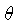 , a igualdade
precisa ser exata para cada potência de
, a igualdade
precisa ser exata para cada potência de
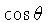 :
:
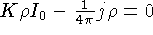 |
(1.43) |
e obtemos a fórmula de recorrência, para 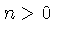 :
:
Para estimar a convergência, estimemos:
obtemos
já que
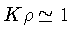 cm-1, e o raio do Sol é
cm-1, e o raio do Sol é
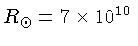 cm.
Portanto, a série (1.42) converge rapidamente no interior
estelar. Podemos portanto nos restringir aos dois primeiros
termos da série (1.42); não podemos usar somente o
primeiro termo porque teríamos caído novamente
na condição de isotropia do campo de radiação,
sem qualquer fluxo resultante.
Esta condição é chamada de equilíbrio termodinâmico
local, já que a diferença do equilíbrio termodinâmico
é tão pequena. Isto é, localmente, as
condições no interior das estrelas podem ser
consideradas em equilíbrio termodinâmico. Neste caso,
não precisamos levar em consideração as transições
dos elementos, porque todas as populações dos níveis
dependem de só um parâmetro, a temperatura cinética
dos elétrons.
Introduzindo os dois
primeiros termos da série (1.42) nas equações
(1.37) a (1.39) para os três momentos, obtemos:
cm.
Portanto, a série (1.42) converge rapidamente no interior
estelar. Podemos portanto nos restringir aos dois primeiros
termos da série (1.42); não podemos usar somente o
primeiro termo porque teríamos caído novamente
na condição de isotropia do campo de radiação,
sem qualquer fluxo resultante.
Esta condição é chamada de equilíbrio termodinâmico
local, já que a diferença do equilíbrio termodinâmico
é tão pequena. Isto é, localmente, as
condições no interior das estrelas podem ser
consideradas em equilíbrio termodinâmico. Neste caso,
não precisamos levar em consideração as transições
dos elementos, porque todas as populações dos níveis
dependem de só um parâmetro, a temperatura cinética
dos elétrons.
Introduzindo os dois
primeiros termos da série (1.42) nas equações
(1.37) a (1.39) para os três momentos, obtemos:
já que
Como
e
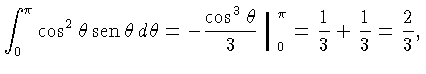 |
(1.44) |
obtemos:
Para a pressão de radiação (1.39):
Usando (1.44) e
obtemos:
de onde segue que:
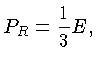 |
(1.45) |
onde 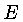 é a energia do campo de radiação por unidade de volume.
O erro relativo nesta relação será da ordem de
é a energia do campo de radiação por unidade de volume.
O erro relativo nesta relação será da ordem de 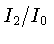 ,
da ordem de
,
da ordem de 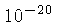 , portanto com precisão suficiente. A equação
(1.45) é a relação adicional que, junto com as
relações (1.40) e (1.41),
completam o conjunto de três equações para
os três momentos.
, portanto com precisão suficiente. A equação
(1.45) é a relação adicional que, junto com as
relações (1.40) e (1.41),
completam o conjunto de três equações para
os três momentos.
Com a ajuda da equação (1.45), podemos agora simplificar
as duas equações diferenciais (1.40) e (1.41).
Primeiro, vamos substituir o fluxo por unidade de área, 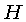 ,
pelo fluxo por toda a esfera, a luminosidade
,
pelo fluxo por toda a esfera, a luminosidade 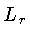 , usando a
relação geométrica:
, usando a
relação geométrica:
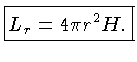 |
(1.46) |
Agora precisamos introduzir uma expressão para a emissividade 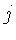 .
A emissão consiste de duas partes; a primeira contribuição
vem da emissão térmica normal, que, de acordo com a lei
de Kirchhoff, é proporcional ao coeficiente de absorção
.
A emissão consiste de duas partes; a primeira contribuição
vem da emissão térmica normal, que, de acordo com a lei
de Kirchhoff, é proporcional ao coeficiente de absorção
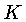 , à constante de Stefan-Boltzmann
, à constante de Stefan-Boltzmann 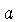 , à velocidade da
luz
, à velocidade da
luz 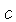 , e à quarta potência da temperatura
, e à quarta potência da temperatura 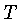 do gás
emitente. Isto porque, em equilíbrio térmico, podemos usar
a relação (1.43):
do gás
emitente. Isto porque, em equilíbrio térmico, podemos usar
a relação (1.43):
e
Como
A segunda contribuição vem dos processos nucleares, e é
igual à produção de energia nuclear por unidade de massa,
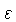 . A expressão completa para a emissividade então
é dada por:
. A expressão completa para a emissividade então
é dada por:
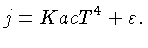 |
(1.47) |
Finalmente, podemos eliminar
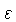 com a ajuda da condição
de equilíbrio radiativo (1.34) na equação (1.40):
com a ajuda da condição
de equilíbrio radiativo (1.34) na equação (1.40):
Como
Como, pela equação (1.34):
Obtemos:
eliminando 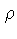 :
:
e usando a relação para a emissividade (1.47), obtemos:
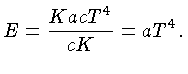 |
(1.48) |
Substituindo-se (1.48) na relação entre a pressão
de radiação e a densidade de energia (1.45):
obtemos uma forma simples para a pressão de radiação:
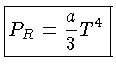 |
(1.49) |
Introduzindo-se (1.45)
na equação (1.41), que anula o segundo termo, obtemos:
Como, da equação (1.48):
obtemos:
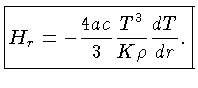 |
(1.50) |
Substituindo-se a relação (1.46), obtemos finalmente:
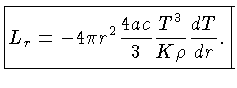 |
(1.51) |
Esta é a nossa quarta equação básica de equilíbrio.
Ela fixa o valor do fluxo líquido de radiação como uma
função do gradiente de temperatura e da opacidade
dos gases através dos quais a radiação passa.





Próxima: Ordem de Grandeza da Luminosidade
Volta: Interiores Estelares
Anterior: A Equação de Transporte Radiativo
©
Modificada em 12 Maio 1999
![]() , que representa a distribuição
de radiação para cada direção, vamos considerar
os três primeiros momentos da distribuição,
a densidade de energia
, que representa a distribuição
de radiação para cada direção, vamos considerar
os três primeiros momentos da distribuição,
a densidade de energia
![]() , o fluxo da radiação
-->
, o fluxo da radiação
-->
![]() , e a pressão de radiação
, e a pressão de radiação ![]() .
.
![]() , por unidade de área,
por unidade de tempo, por unidade de ângulo sólido. O
fluxo é a energia, por unidade de área,
por unidade de tempo,
em todas as direções:
, por unidade de área,
por unidade de tempo, por unidade de ângulo sólido. O
fluxo é a energia, por unidade de área,
por unidade de tempo,
em todas as direções:
![]() , obtemos:
, obtemos:
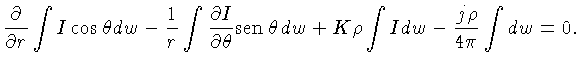
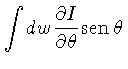

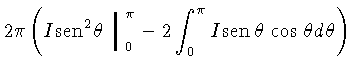
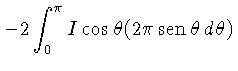
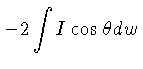
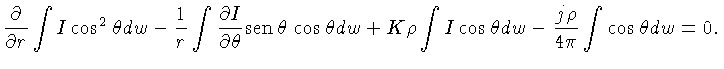

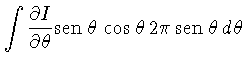
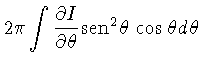
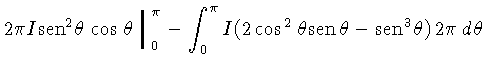
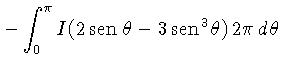
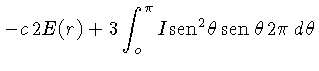
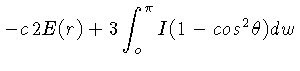
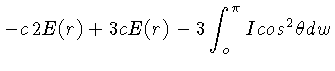
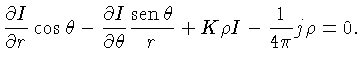
![\frac{\partial}{\partial r}\left(I_0 + I_n\cos^n\theta\right) +
\...
...rm{sen}^2\theta\right]+K\rho I_0 +K\rho I_n\cos^n\theta-
\frac{1}{4\pi}j\rho=0,$](img347.gif)
![$ \frac{\partial}{\partial r}\left(I_0 + I_n\cos^n\theta\right) +
\...
...1-cos^2\theta)\right]+K\rho I_0 +
K\rho I_n\cos^n\theta- \frac{1}{4\pi}j\rho=0,$](img348.gif)
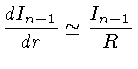
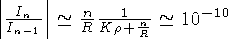
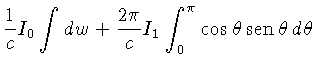
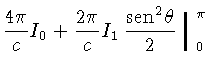
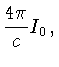
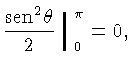
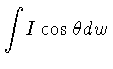
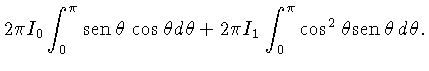
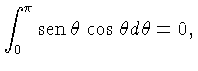
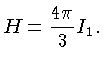
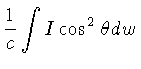
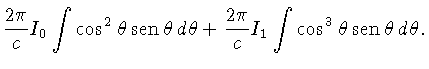
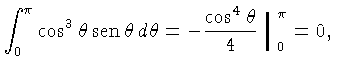
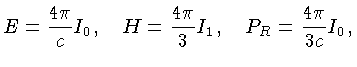
![]() ,
pelo fluxo por toda a esfera, a luminosidade
,
pelo fluxo por toda a esfera, a luminosidade ![]() , usando a
relação geométrica:
, usando a
relação geométrica:
![]() .
A emissão consiste de duas partes; a primeira contribuição
vem da emissão térmica normal, que, de acordo com a lei
de Kirchhoff, é proporcional ao coeficiente de absorção
.
A emissão consiste de duas partes; a primeira contribuição
vem da emissão térmica normal, que, de acordo com a lei
de Kirchhoff, é proporcional ao coeficiente de absorção
![]() , à constante de Stefan-Boltzmann
, à constante de Stefan-Boltzmann ![]() , à velocidade da
luz
, à velocidade da
luz ![]() , e à quarta potência da temperatura
, e à quarta potência da temperatura ![]() do gás
emitente. Isto porque, em equilíbrio térmico, podemos usar
a relação (1.43):
do gás
emitente. Isto porque, em equilíbrio térmico, podemos usar
a relação (1.43):
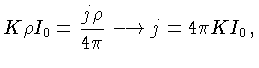
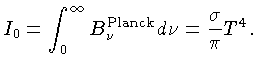
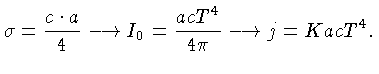
![]() . A expressão completa para a emissividade então
é dada por:
. A expressão completa para a emissividade então
é dada por:
![]() com a ajuda da condição
de equilíbrio radiativo (1.34) na equação (1.40):
com a ajuda da condição
de equilíbrio radiativo (1.34) na equação (1.40):