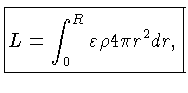Próxima: O Transporte de Energia Radiativo Volta: Interiores Estelares Anterior: Energia Nuclear

Condição de Equilíbrio Térmico

Discutímos na seção anterior que a perda de energia na superfície por radiação é compensada pela liberação de energia por processos nucleares no interior da estrela.

Esta condição pode ser expressa como:

$${L = \int_0^R \varepsilon \rho 4 \pi r^2 dr,}$$ (1.33)

onde $\varepsilon$ é a energia liberada por processos nucleares, por unidade de massa e por unidade de tempo, excluindo-se as perdas por neutrinos. A produção de energia nuclear $\varepsilon$ depende da temperatura, densidade e composição.

Nosso tratamento da radiação pode ser macroscópico, isto é, não é necessário levar em conta os efeitos quânticos da radiação. A radiação é tratada como um fluído. Entretanto, quando tratarmos da interação da radiação com a matéria, precisaremos adotar uma descrição quântica. Será que a condição de equilíbrio térmico precisa ser satisfeita minuto a minuto, como a condição de equilíbrio hidrostático? Não. Se desligássemos a produção de energia nuclear do Sol, ele continuaria a brilhar, alimentando-se de sua energia gravitacional. Se tornássemos a ligar a geração de energia nuclear em um tempo menor do que o tempo de contração de Kelvin, o Sol não teria sido afetado seriamente pela interferência. Por estes períodos, as energias gravitacional e térmica agem como um reservatório. Entretanto, para tempos maiores do que o tempo de contração de Kelvin, a condição (1.33) precisa ser satisfeita.

A equação (1.33) garante o balanço de energia para a estrela como um todo. Mas o mesmo tipo de balanço tem que ser satisfeito em cada camada da estrela. Um ganho de energia por uma camada e uma perda de energia em outra camada levaria à mudança na estrutura de temperatura no interior da estrela, e portanto tornaria a estrela instável. Consideremos uma camada esférica de raio $r$ e espessura unitária. O balanço de energia nesta camada pode ser escrito como:

$$\frac{dL_r}{dr} = \varepsilon \rho 4\pi r^2$$ (1.34)

onde $L_r$ é o fluxo de energia através da esfera de raio $r$. O termo da esquerda desta equação representa a perda líquida de energia da camada causada pelo excesso de fluxo deixando a superfície externa, em relação ao fluxo de energia entrando pela superfície interna. O termo da direita representa a energia produzida na camada por processos nucleares.

Uma derivação mais formal usa a definição de fluxo, $\vec{F}$, que é o vetor do fluxo de energia total (energia por unidade de área), e $\varepsilon$ a energia total gerada perto do ponto $r$, por todas as fontes, por unidade de massa e por unidade de tempo. O estado estacionário (invariança) requer que:

$\oint_S \vec{F}\cdot d\vec{s} = \int_V \rho \varepsilon dV,$

onde $d\vec{s}$ é o elemento de área, e $dV$ o elemento de volume. Pelo teorema da divergência,

$\vec{\nabla}\cdot \vec{F} = \rho \varepsilon.$

Assumindo simetria esférica, $\vec{F}$ é somente radial, de modo que:

$\vec{\nabla}\cdot \vec{F} = \frac{1}{r^2}\frac{d}{dr}(r^2 F\...t) = \frac{1}{4\pi r^2} \frac{d}{dr}(4\pi r^2 F) = \rho \varepsilon.$

Como $L_r \equiv 4\pi r^2 F$, temos:

$$\frac{dL_r}{dr} = 4\pi r^2 \rho \varepsilon,$$

reproduzindo a equação (1.34), que representa a terceira das condições básicas que devem ser obedecidas no interior da estrela.

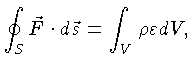
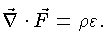
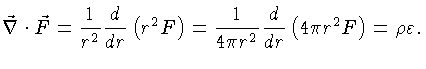
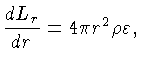
A equação (1.34) precisa ser modificada para as fases curtas mas críticas da evolução estelar em que as mudanças da estrutura interna são tão rápidas que as variações nos dois reservatórios menores de energia estelar - térmica e gravitacional - são importantes. Nestas fases, não podemos esperar que o fluxo carregue para fora do volume exatamente a energia gerada por segundo por reações nucleares dentro do volume, como expresso pela relação (1.34). Espera-se que a energia perdida pelo fluxo, a energia gerada pelas reações nucleares, e o trabalho exercido pela pressão, juntos, determinem a taxa de mudança da energia interna do volume. A energia interna por unidade de massa de um gás ideal é dada por $\frac{3k}{2m}T$. O trabalho exercido pela pressão é dado por $-PdV$. A energia nuclear liberada por unidade de massa, por unidade de tempo, é, por definição, $\varepsilon$. A perda líquida de energia, por uma camada esférica de espessura unitária, é $dL_r/dr$, que precisa ser dividida pela massa da camada, $4\pi r^2 \rho$ para dar a perda por unidade de massa. Portanto:

$\frac{d}{dt}(\frac{3}{2}\frac{k}{m}T) = -P\frac{dV}{dt} + \varepsilon - \frac{1}{4\pi r^2 \rho}\frac{dL_r}{dr}$

Como o volume específico pode ser substituído pelo seu recíproco, a densidade,

$V \equiv \frac{1}{\rho} \rightarrow dV = - \frac{1}{\rho^2}d\rho \rightarrow -PdV = + \frac{P}{\rho^2}d\rho,$

obtemos a expressão geral

$\frac{d}{dt}(\frac{3}{2}\frac{k}{m}T) = + \frac{P}{\rho^2}\frac{d\rho}{dt} + \varepsilon - \frac{1}{4\pi r^2 \rho}\frac{dL_r}{dr}$

Usando a equação de estado de um gás ideal (1.25), podemos escrever:

$P = \frac{k}{m}\rho T \rightarrow \frac{k}{m}T=\frac{P}{\rho}$

$\frac{d}{dt}(\frac{3}{2}\frac{P}{\rho}) - \frac{P}{\rho^2}\frac{d\rho}{dt} = \varepsilon - \frac{1}{4\pi r^2 \rho}\frac{dL_r}{dr}.$

Como

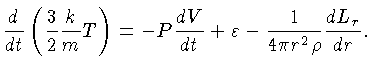
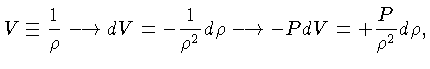
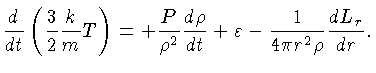
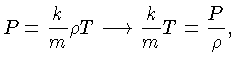
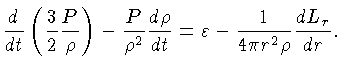
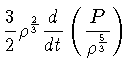$$\frac{3}{2}\rho^{\frac{2}{3}}\frac{d}{dt}(\frac{P}{\rho^{\frac{5}{3}}}) \frac{3}{2}\rho^{\frac{2}{3}}[\frac{1}{\rho^{\frac{2}{3}}}\f...) + \frac{P}{\rho}\frac{d}{dt}\(\frac{1}{\rho^{\frac{2}{3}}}) ]$$

$$\frac{3}{2}\frac{d}{dt}(\frac{P}{\rho}) + \frac{3}{2}\...c{1}{3}}P(-\frac{2}{3})\frac{1}{\rho^{\frac{5}{3}}} \frac{d\rho}{dt}$$

$$\frac{3}{2}\frac{d}{dt}(\frac{P}{\rho})- \frac{P}{\rho^2}\frac{d\rho}{dt}.$$

é igual ao termo da esquerda, podemos escrever:

$\frac{3}{2}\rho^{\frac{2}{3}}\frac{d}{dt}(\frac{P}{\rho^{\frac{5}{3}}}) =\varepsilon - \frac{1}{4\pi r^2 \rho}\frac{dL_r}{dr},$

ou

$${\frac{dL_r}{dr}=4\pi r^2\rho[\varepsilon-\frac{3}{2}\rho^{\frac{2}{3}}\frac{d}{dt}(\frac{P}{\rho^{\frac{5}{3}}})]}$$ (1.35)

Esta equação deve ser usada em lugar da equação (1.34) durante as fases em que as mudanças evolucionárias são significativas. Ela é idêntica à (1.34) nas fases normais, em que as mudanças são tão lentas que o termo com a derivada temporal na equação (1.35) pode ser desprezado.

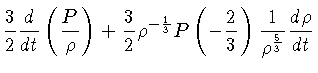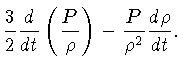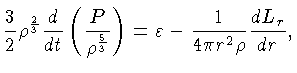
Até agora somente consideramos a condição que o fluxo de energia deve obedecer para balançar a produção de energia. Fisicamente, entretanto, o fluxo é determinando pelos mecanismos de transporte de energia, que podem ser condução (transporte de energia através dos corpos), convecção (transporte de energia pelo movimento dos corpos), ou radiação (transporte de energia pelo campo eletromagnético). Para qualquer destes três mecanismos, é o gradiente de temperatura que essencialmente determina o fluxo de energia. Portanto precisamos considerar estes mecanismos em detalhe para determinar o gradiente de temperatura que irá produzir um fluxo que obedeça à condição (1.34) ou (1.35).

Como o livre caminho médio dos íons e elétrons é tão pequeno, comparados com o raio estelar, a condução pode ser desprezada nas estrelas normais. Existem condições especiais, como o caso de gás degenerado, no interior de estrelas anãs brancas e estrelas de nêutrons, e mesmo no núcleo de gigantes vermelhas, em que o livre caminho médio dos elétrons é muito grande, e a condução por elétrons muito efetiva.

Nas próximas seções, consideraremos em detalhe os dois mecanismos de transporte de energia que dominam no interior da maioria das estrelas, radiação e convecção.

Próxima: O Transporte de Energia Radiativo Volta: Interiores Estelares Anterior: Energia Nuclear