




Próxima: Geração de Energia Nuclear
Volta: Opacidades
Anterior: Espalhamento Thomson
Finalmente, o coeficiente total de absorção por unidade de massa,
levando-se em conta o espalhamento coerente e a
emissão induzida,
pode ser escrito como:
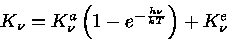 |
(1) |
A emissão induzida leva em conta que se uma radiação
de freqüência 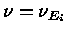 incide sobre um átomo já no
estado
incide sobre um átomo já no
estado 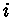 , a probabilidade de emissão de radiação nessa
freqüência será aumentada. O excesso de probabilidade
é proporcional à intensidade
, a probabilidade de emissão de radiação nessa
freqüência será aumentada. O excesso de probabilidade
é proporcional à intensidade 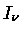 da radiação
incidente, como determinado por Einstein em 1917, em sua
derivação da lei de Planck.
da radiação
incidente, como determinado por Einstein em 1917, em sua
derivação da lei de Planck.
Podemos obter fórmulas aproximadas para os coeficientes
de absorção, no caso de ionização completa:
 \bar{g}_{ff} F'(\rho,T)\frac{\rho}{T_6^{3,5}}~{cm^2/g}}](img5.gif) |
(2) |
onde
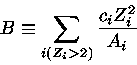 |
(3) |
e
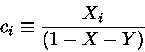 |
(4) |
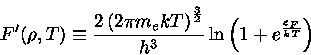 |
(5) |
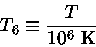 |
(6) |
e
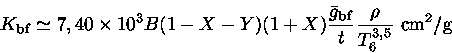 |
(7) |
onde 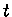 é chamado de fator de guilhotina
é chamado de fator de guilhotina
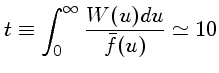 |
(8) |
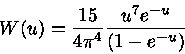 |
(9) |
com
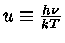 ,
,
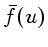 uma média de
uma média de
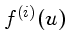 sobre todos os elementos
relevantes exceto H e He de
e
sobre todos os elementos
relevantes exceto H e He de
e
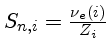 a carga efetiva.
a carga efetiva.
Como o coeficiente numérico de 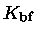 é muito
maior do que o coeficiente de
é muito
maior do que o coeficiente de 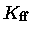 , o coeficiente
de
absorção ligado-livre domina sobre o coeficiente
livre-livre no interior estelar, se a abundância
dos elementos pesados
, o coeficiente
de
absorção ligado-livre domina sobre o coeficiente
livre-livre no interior estelar, se a abundância
dos elementos pesados 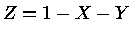 for grande o suficiente.
Se usarmos
for grande o suficiente.
Se usarmos
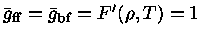 ,
,
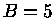 e
e 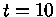 , obtemos a condição
, obtemos a condição
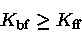 |
(10) |
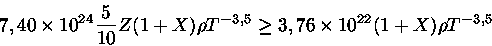 |
(11) |
ou seja
isto é, a opacidade ligado-livre domina sobre a livre-livre
para estrelas de População I, como o Sol.
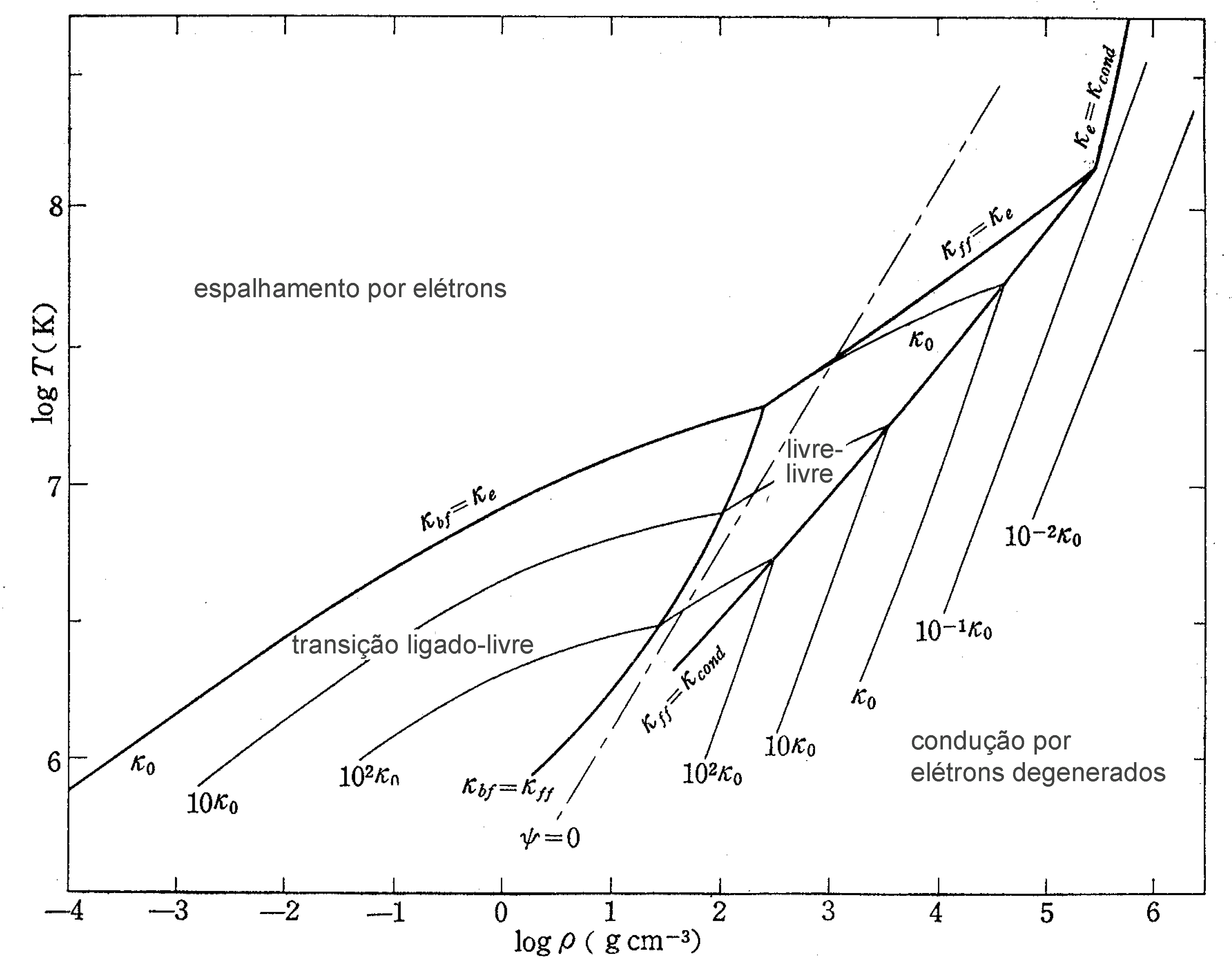
Figura publicada por Chushiro Hayashi, Minoru Nishida e Daiichiro Sugimoto
(1962, Progress of Theoretical Physics Supplement,
22, 1) ilustrando as regiões onde cada tipo de opacidade é mais
importante, em função da temperatura e densidade.
Já a condição
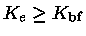 ,
assumindo
,
assumindo
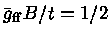 , se dá com:
, se dá com:
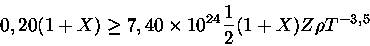 |
(12) |
ou
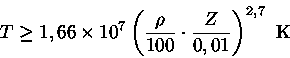 |
(13) |
isto é, para
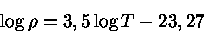 |
(14) |
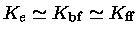 , para
, para 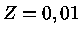 .
Portanto, para densidades
.
Portanto, para densidades
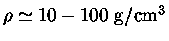 ,
normais nos interiores estelares, o espalhamento por
elétrons domina para
,
normais nos interiores estelares, o espalhamento por
elétrons domina para 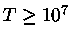 K.
K.
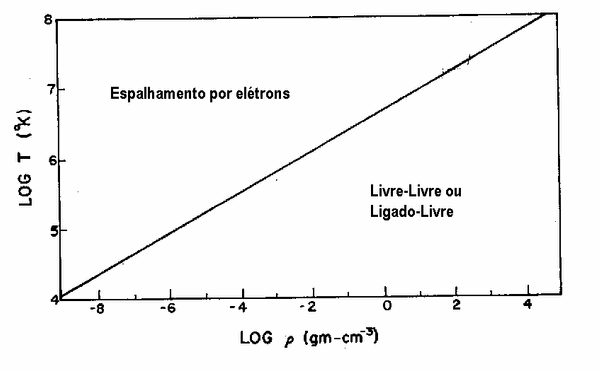
Regiões de domínio dos diferentes tipos de absorção.
Outras componentes que precisam ser levadas em conta são
as transições ligado-ligado, e o
alargamento da
linha por colisão, efeito Doppler (velocidade) e efeito Stark (campo elétrico, proporcional à densidade)
[Johannes Stark (1874-1957),
Beobachtungen über den Effekt des elektrischen Feldes auf Spektrallinien I. Quereffekt
(Observações do efeito do campo elétricos nas linhas espectrais I. Efeito transversal), Annalen der Physik, vol. 43, pp. 965-983 (1914)].
Para estrelas com campos magnéticos fortes, como no caso de estrelas de nêutrons, precisamos levar em conta o efeito Zeeman
[Pieter Zeeman (1865-1943)
(1897, "The Effect of Magnetisation on the Nature of Light Emitted by a Substance", Nature, 55, 347) e
a explicação teórica de seu professor Hendrik Antoon Lorentz (1853-1928)],
já que a propagação ao longo do campo é diferente de perpendicular a ele.
H-
Para temperaturas abaixo de 7000 K, pode formar-se
o íon negativo H-
pois um hidrogênio neutro se polariza se houver uma carga
elétrica próxima, podendo atrair e ligar-se a outro elétron.
A baixas temperaturas,
o íon negativo H-
é a principal fonte de absorção, pois tem um nível
somente 0,754 eV acima do fundamental, que corresponde a
um fóton de
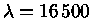 Å. Para que exista o íon,
é necessária a presença de hidrogênio neutro e elétrons
livres.
O número de íons negativos de hidrogênio em equilíbrio
é dado pela
lei de Saha, onde o potencial de ionização
é dado pela energia de ligação do segundo elétron.
A função de partição U-=1
para o íon negativo e U0=2 para o hidrogênio neutro. Logo
a lei de Saha pode ser escrita como
Å. Para que exista o íon,
é necessária a presença de hidrogênio neutro e elétrons
livres.
O número de íons negativos de hidrogênio em equilíbrio
é dado pela
lei de Saha, onde o potencial de ionização
é dado pela energia de ligação do segundo elétron.
A função de partição U-=1
para o íon negativo e U0=2 para o hidrogênio neutro. Logo
a lei de Saha pode ser escrita como
Os elétrons são provenientes de algum hidrogênio ionizado
e de elétrons das camadas externas de alguns metais abundantes,
como Na, K, Ca e Al. Portanto, a opacidade do 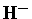 depende
não somente da temperatura, mas da abundância dos metais. Para
depende
não somente da temperatura, mas da abundância dos metais. Para
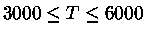 K, densidades de
K, densidades de
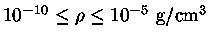 , uma estimativa
da opacidade é
, uma estimativa
da opacidade é
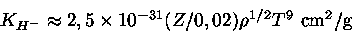 |
(15) |
Para temperaturas
abaixo de 5000 K, as absorções moleculares são muito importantes.
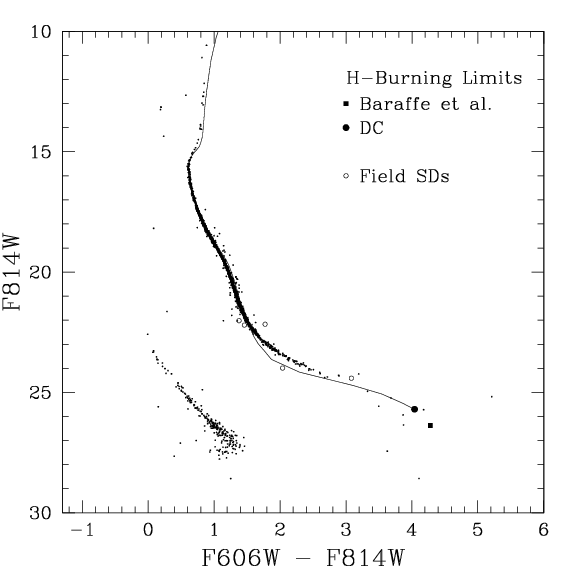
Diagrama cor-magnitude do aglomerado globular NGC 6397 obtido por
Harvey B. Richer, Aaron Dotter, Jarrod Hurley, Jay Anderson, Ivan King, Saul Davis, Gregory G. Fahlman, Brad M. S. Hansen, Jason Kalirai, Nathaniel Paust, R. Michael Rich & Michael M. Shara
(2008, Astronomical Journal, 135, 2141),
combinando 126 órbitas do Hubble Space Telescope com a Advanced Camera for Surveys.
O limite mínimo de queima de hidrogênio de
Baraffe, I. et al. 1997 (A&A, 327, 1054)
e de
Dotter, A., Chaboyer, B., Jevremovic, D., Baron, E., Ferguson, J. W.,
Sarajedini, A., & Anderson, J. 2007 (AJ, 134, 376)
estão representados por um quadrado e por um círculo fechado.
Somente os modelos mais recentes incluem
as opacidades moleculares
necessárias para explicar a cor das estrelas próximas do limite de
queima de hidrogênio (0,08 MSol), observadas por exemplo
com o Telescópio Espacial Hubble nos cúmulos globulares NGC 6397
e M4, e também as estrelas mais vermelhas do ramo das supergigantes (AGB)
[Jason W. Ferguson & Aaron Dotter, 2008,
The Art of Modeling Stars in the 21st Century, Proceedings of the International Astronomical Union, IAU Symposium, Volume 252, p. 1;
Aaron Dotter,
Brian Chaboyer,
Darko Jevremovic,
Veselin Kostov,
E. Baron, &
Jason W. Ferguson, 2008, The Dartmouth Stellar Evolution Database,
Astrophysical Journal Supplement, 178, 89;
Paola Marigo, Leo Girardi, Alessandro Bressan et al. 2008,
Astronomy & Astrophysics, 482, 883;
Achim Weiss & James W. Ferguson, 2009,
Astronomy & Astrophysics, 508, 1343].
Yang Chen, Léo Girardi, Alessandro Bressan, Paola Marigo, Mauro Barbieri & Xu Kong,
no artigo de 2014 (2014arXiv1409.0322C) mostram que, mesmo usando
as opacidades moleculares, precisam de uma correção empírica para ajustar
os diagramas cor-magnitude dos aglomerados na parte fria.
Como dissemos antes, freqüentemente se aproxima a opacidade por uma fórmula do tipo:
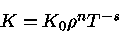 |
(16) |
que, embora não precisas, servem para estimativas. O caso
n=1 e s=3,5, válido para absorção livre-livre em
um gás não-degenerado em que a maioria dos elementos
está completamente ionizado, é chamada de opacidade
de Kramers, pois foi derivada classicamente para as opacidades
livre-livre e ligado-livre pelo
físico holandês Heindrik Anthony Kramers (1894-1952) em 1923.
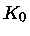 função da composição química,
e
função da composição química,
e 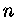 e
e 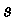 ajustados às tabelas de opacidades. O caso
ajustados às tabelas de opacidades. O caso
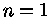 e
e 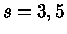 só
é estritamente válido para as transições
livre-livre em um gás não-degenerado basicamente ionizado.
só
é estritamente válido para as transições
livre-livre em um gás não-degenerado basicamente ionizado.
Por condução térmica, o fluxo de energia depende do
gradiente
de temperatura, isto é, o fluxo se dá da região mais quente
para a mais fria,
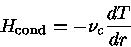 |
(17) |
onde 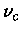 é o coeficiente de condução.
é o coeficiente de condução.
Evry Leon Schatzman (1920-2010) e Françoise Praderie no livro The Stars de 1993,
(Heidelberg, Springer), p. 102, propõe que o coeficiente de
difusão dos elétrons, responsáveis pela condução,
para um plasma fracamente correlacionado, é dado por
onde 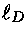 é o comprimento de Debye [Peter Joseph William Debye (1884-1966)] e
Podemos modificar a definição de opacidade, definindo uma
opacidade efetiva total:
é o comprimento de Debye [Peter Joseph William Debye (1884-1966)] e
Podemos modificar a definição de opacidade, definindo uma
opacidade efetiva total:
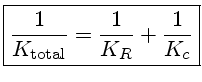 |
(18) |
onde 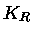 é a opacidade radiativa, e
é a opacidade radiativa, e 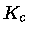 a opacidade
conductiva, definida de modo que:
a opacidade
conductiva, definida de modo que:
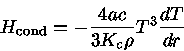 |
(19) |
ou seja:
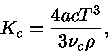 |
(20) |
e, portanto, o fluxo total
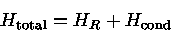 |
(21) |
pode ser escrito usando-se a equação do equilíbrio
radiativo (1.51), substituindo-se 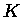 por
por
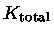 .
.
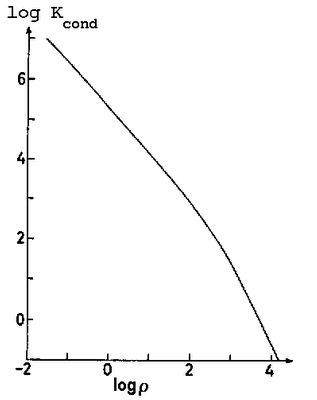
Valores da
opacidade conductiva,
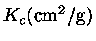
, para
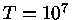
K.
Embora a condução não seja um mecanismo importante de transporte
de energia para estrelas na seqüência principal, ela é importante
no núcleo de estrelas anãs brancas e de algumas supergigantes
vermelhas, onde os elétrons estão degenerados.
Como nenhum processo envolvendo colisão de um elétron degenerado
pode espalhar o elétron para um estado de energia já ocupado,
somente os elétrons próximos do topo do mar de Fermi podem
participar efetivamente no processo de condução. O mecanismo
mais eficiente de espalhamento dos elétrons é através
da interação coulombiana com os íons do meio,
e, portanto, a opacidade conductiva depende da carga dos íons, 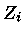 .
.
Em 1950, Leon Mestel calculou o coeficiente condutivo para o
caso de elétrons não-relativísticos,
obtendo
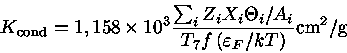 |
(22) |
onde
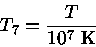 |
(23) |
O fator
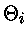 leva em conta os
efeitos dos encontros distantes dos elétrons e íons
leva em conta os
efeitos dos encontros distantes dos elétrons e íons
![\Theta_i = \ln [\frac{2}{1-\cos \theta_i}]^\frac{1}{2} \simeq 1](img63.gif) |
(24) |
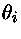 também é função da degenerescência e precisa ser
calculado numericamente, como
também é função da degenerescência e precisa ser
calculado numericamente, como
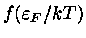 :
:
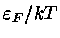 |
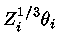 |
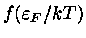 |
| -4 |
0,15479 |
0,4369 |
| -0,2 |
0,48637 |
17,67 |
| 4 |
0,77132 |
367,9 |
| 8 |
0,82284 |
2001 |
Para pequena degenerescência,
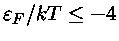 ,
Para grande degenerescência,
,
Para grande degenerescência,
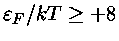 ,
,
Uma estimativa mais simples é
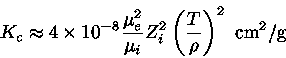 |
(25) |
Essa opacidade também depende da carga dos íons,
pois os elétrons são acelerados em interações
com os íons.
Como um exemplo de onde a opacidade conductiva é importante,
consideremos o interior de uma anã branca fria, com
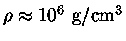 ,
,
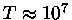 K,
e uma composição de carbono.
Como o carbono estará ionizado,
a opacidade radiativa será dada por
espalhamento de elétrons
K,
e uma composição de carbono.
Como o carbono estará ionizado,
a opacidade radiativa será dada por
espalhamento de elétrons
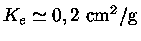 .
.
A opacidade conductiva (25),
com 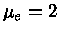 ,
, 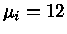 e
e 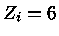 , será de
, será de
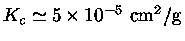 .
.
Como
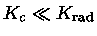 ,
,
 ,
usando-se equação (18).
Portanto, o transporte de energia
se dará por condução, e não por radiação.
Note que neste caso o menor coeficiente é dominante,
o oposto do que ocorre com a opacidade real.
,
usando-se equação (18).
Portanto, o transporte de energia
se dará por condução, e não por radiação.
Note que neste caso o menor coeficiente é dominante,
o oposto do que ocorre com a opacidade real.
Alexander Yurievich
Potekhin
atualizou em 2006-2008 seus cálculos das
opacidades conductivas para casos parcialmente e
completamente degenerados, e disponibiliza um
programa em fortran
para seu cálculo.
Santi Cassisi,
Alexander Yurievich Potekhin,
Adriano Pietrinferni,
Márcio Catelan
& Maurizio Salaris publicaram
"Updated Electron-Conduction Opacities: The Impact on Low-Mass Stellar Models", em
2007 no Astrophysical Journal, 661, 1094.
Os modelos PARSEC utilizam as
opacidades condutivas de
Naoki Itoh, Shinsuke Uchida, Yu Sakamoto, Yasuharu Kohyama & Satoshi Nozawa, 2008,
The Second Born Corrections to the Electrical and Thermal Conductivities of Dense Matter in the Liquid Metal Phase,
Astrophysical Journal, 677, 495.
Os cálculos de opacidades são bastante complexos,
pois dependem da física estatística e da física de
partículas
e variam
de acordo com a composição química do modelo.
Os modelos até o início dos anos 1990 utilizavam as tabelas
do astrônomo americano
Arthur Nelson Cox (1927-2013) e
James Edward Tabor (1931-1989)
do Los Alamos National Laboratory,
publicadas em 1976 no Astrophysical Journal Supplement, 31, 271.
Em 1990,
Carlos A. Iglesias,
Forrest J. Rogers (1938-2013) e Brian G. Wilson,
do Lawrence Livermore National Laboratory,
publicaram no Astrophysical Journal, 360, 281,
as tabelas do projeto OPAL,
atualizadas em 1996 por
Carlos A. Iglesias e Forrest J. Rogers
no Astrophysical Journal, 464, 943
e novamente em 2006.
As tabelas OPAL
incluem correções de muito corpos, degenerescência dos
elétrons, difração quântica e acoplamento de plasma.
Só com estas correções foi possível modelar as
pulsações das estrelas RR Lyrae e Delta Scuti com precisão,
já que para alguns valores de T×ρ, estas opacidades são
um fator de 3× maiores do que as anteriores.
Somente a aproximação hidrogênica (duas partículas)
pode ser calculada analiticamente. Para todos os outros átomos,
o cálculo tem de ser por aproximação.
Por exemplo, o 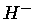 tem um nível de energia 0,75 eV acima do nível
fundamental do hidrogênio neutro, mas esse nível só
pode ser calculado por aproximação não-hidrogênica.
As tabelas e programas de interpolação podem ser acessados também neste link,
e as versões atuais incluem correções nas opacidades conductivas de
Potekhin et al. (2006) e as moleculares de Ferguson et al. (2005,
Astrophysical Journal, 623, 585).
tem um nível de energia 0,75 eV acima do nível
fundamental do hidrogênio neutro, mas esse nível só
pode ser calculado por aproximação não-hidrogênica.
As tabelas e programas de interpolação podem ser acessados também neste link,
e as versões atuais incluem correções nas opacidades conductivas de
Potekhin et al. (2006) e as moleculares de Ferguson et al. (2005,
Astrophysical Journal, 623, 585).
Table:
Estrelas Variáveis
| Tipo |
Período |
População |
Tipo Espectral |
Mag. Absoluta |
| RR Lyrae |
1,5 a 24 h |
Pop. II |
A2-F2 |
0,6 |
| Cefeidas |
1 a 50 d |
Pop. I |
F6-K2 |
-6 a -0,5 |
| W Virg |
2 a 45 d |
Pop. II |
F2-G6 |
-3 a 0 |
| Miras |
100 a 700 d |
I e II |
M,T |
-2 a 1 |
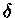 Scuti Scuti |
0,5 a 5 h |
Pop. I |
A5-F5 |
2 a 3 |
Outro projeto que calcula as opacidades chama-se
Opacity Project.,
liderado por
Michael J. Seaton (1923-2007) do University College London
Em 2005, ele publica no Monthly Notices of the Royal Astronomical Society, 362, L1 o coeficiente de absorção monocromática
para 17 elementos: H, He, C, N, O, Ne, Na, Mg, Al, Si, S, Ar, Ca,
Cr, Mn, Fe e Ni, incluindo transições de elétrons internos
(inner shell)
com um arquivo dos dados e programa para
calcular a opacidade média de Rosseland, para composições
químicas diferentes e temperaturas e pressões diferentes.
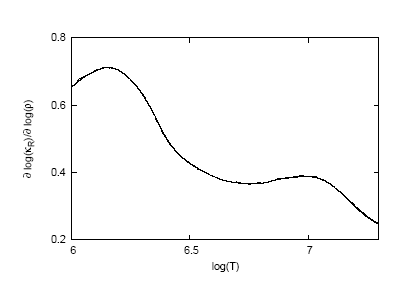
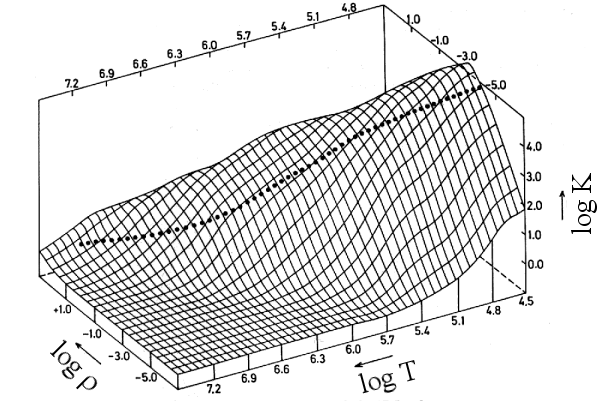
Um exemplo dos resultados para uma composição química específica e uma
densidade específica.
Michael J. Seaton e Nigel R. Badnell
(2004, Monthly Notices of the Royal Astronomical Society, 354, 457)
apresentam uma comparação entre os resultados dos dois projetos,
mostrando que os resultados são bastante similares, dentro
de 5%, mas diferenças maiores que
30% entre OP e OPAL estão presentes para T=3×105K; ρ10-5 g/cm3,
exatamente a local do
Z-bump (excesso por Z), onde o aumento na opacidade local produz as condições
para a excitação de pulsações observadas em estrelas tipo B e subanãs (sdB).
Naturalmente as opacidades totais dependem da composição química assumida.
A maior parte dos cálculos ainda está feita com a composição solar
de Nicolas Grevesse e Arlette Noels (1993). Algums modelos
foram calculadas
para a composição de Martin Asplund, Nicolas Grevesse e A. Jacques Sauval (2005).
Por exemplo, este link contem o coeficiente de Rossland para composição de Martin Asplund, Nicolas Grevesse e
A. Jacques Sauval (2005).
Mas os resultados de heliosismologia não concordam com os valores da
abundância de hélio de 2005.
A mais recente determinação das abundâncias solares é
Nicolas Grevesse, Martin Asplund, A. Jacques Sauval & Pat Scott, 2010,
Astrophysics & Space Science, 328, 179,
obtendo X=0,7380, Y=0,2485 e Z=0,0134, consistente com a
heliosismologia.
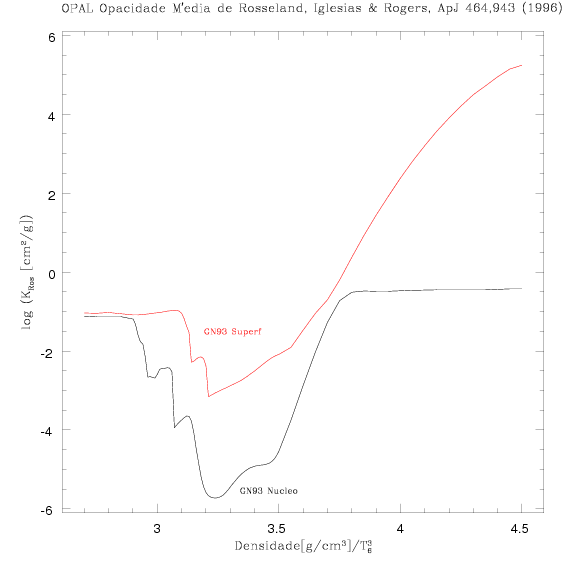
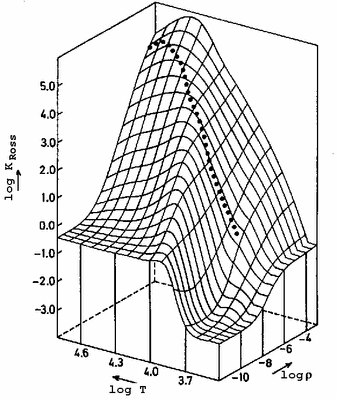
Opacidade média de Rosseland para X=0,8 e Z=0,002. T
6 é T/(1 000 000 K).
Os modelos PARSEC:
PAdova and TRieste Stellar Evolution Code
de
Alessandro Bressan, Paola Marigo, Léo Girardi, Bernardo Salasnich, Claudia Dal Cero, Stefano Rubele & Ambra Nanni,
publicados em
2012 no Monthly Notices of the Royal Astronomical Society, 427, 127, foram calculados para z=0,0152 (Elisabetta Caffau et al. 2011),
mas acoplados com o projeto OPAL, permitem calcular a opacidade para qualquer composição química consistentemente.
Estes modelos, de 0,1 a 12 massas solares, incluem a fase de pré-sequêncial principal, e evoluem até o início dos
pulsos térmicos ou ignição do carbono.





Próxima: Exemplos de opacidades
Volta: Opacidades
Anterior: Espalhamento Thomson
 Evolução Estelar
Evolução Estelar

©
Modificada em 15 set 2014
 \bar{g}_{ff} F'(\rho,T)\frac{\rho}{T_6^{3,5}}~{cm^2/g}}](img5.gif)
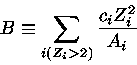
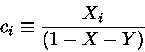
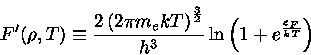
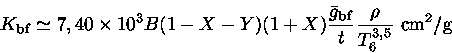
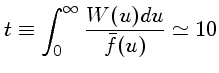
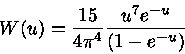
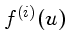 sobre todos os elementos
relevantes exceto H e He de
sobre todos os elementos
relevantes exceto H e He de
![$f^{(i)}(u) \equiv \sum_n \frac{2\pi^2 e^4 m_e Z_i^2}{n^2h^2kT}
...S_{n,i}^4}{n^3}[\frac{2\left(2\pi m_ekT\right)^{3/2}n_n^i}{n_eh^3}]$](imgui4.gif)
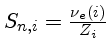 a carga efetiva.
a carga efetiva.
![]() é muito
maior do que o coeficiente de
é muito
maior do que o coeficiente de ![]() , o coeficiente
de
absorção ligado-livre domina sobre o coeficiente
livre-livre no interior estelar, se a abundância
dos elementos pesados
, o coeficiente
de
absorção ligado-livre domina sobre o coeficiente
livre-livre no interior estelar, se a abundância
dos elementos pesados ![]() for grande o suficiente.
Se usarmos
for grande o suficiente.
Se usarmos
![]() ,
,
![]() e
e ![]() , obtemos a condição
, obtemos a condição

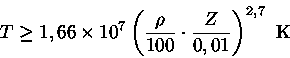
![]() Å. Para que exista o íon,
é necessária a presença de hidrogênio neutro e elétrons
livres.
O número de íons negativos de hidrogênio em equilíbrio
é dado pela
lei de Saha, onde o potencial de ionização
é dado pela energia de ligação do segundo elétron.
A função de partição U-=1
para o íon negativo e U0=2 para o hidrogênio neutro. Logo
a lei de Saha pode ser escrita como
Å. Para que exista o íon,
é necessária a presença de hidrogênio neutro e elétrons
livres.
O número de íons negativos de hidrogênio em equilíbrio
é dado pela
lei de Saha, onde o potencial de ionização
é dado pela energia de ligação do segundo elétron.
A função de partição U-=1
para o íon negativo e U0=2 para o hidrogênio neutro. Logo
a lei de Saha pode ser escrita como
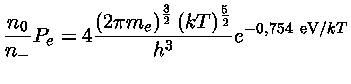

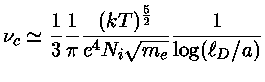
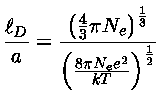
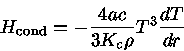
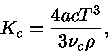
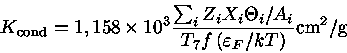
![\Theta_i = \ln [\frac{2}{1-\cos \theta_i}]^\frac{1}{2} \simeq 1](img63.gif)
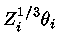
![$\theta_i \simeq 0,589 [e^(\varepsilon_F/kT)]^\frac{1}{3}/Z_i^\frac{1}{3}$](theta1.gif)
![$\theta_i \simeq 0,848 [1-2,06(\varepsilon_F/kT)^{-2}]/Z_i^\frac{1}{3}$](theta2.gif)
![]() ,
,
![]() K,
e uma composição de carbono.
Como o carbono estará ionizado,
a opacidade radiativa será dada por
espalhamento de elétrons
K,
e uma composição de carbono.
Como o carbono estará ionizado,
a opacidade radiativa será dada por
espalhamento de elétrons
![]() .
.
![]() ,
, ![]() e
e ![]() , será de
, será de
![]() .
.
![]() ,
,
![]() ,
usando-se equação (18).
Portanto, o transporte de energia
se dará por condução, e não por radiação.
Note que neste caso o menor coeficiente é dominante,
o oposto do que ocorre com a opacidade real.
,
usando-se equação (18).
Portanto, o transporte de energia
se dará por condução, e não por radiação.
Note que neste caso o menor coeficiente é dominante,
o oposto do que ocorre com a opacidade real.


![]()