6 FACTOR DE EMISIONES ESTIMULADAS
De acuerdo a lo expresado en la sección precedente, el número de emisiones espontáneas del nivel i al j por unidad de tiempo, unidad de ángulo sólido y unidad de volumen es
![]() ,
,
en tanto que
![]()
y
![]() representan
respectivamente los números de absorciones negativas y absorciones verdaderas,
por segundo, unidad de ángulo sólido y unidad de volumen. Si suponemos que
estamos en condiciones de equilibrio
térmico, las poblaciones relativas de los dos niveles de energía
considerados verifican la ley de Boltzmann :
representan
respectivamente los números de absorciones negativas y absorciones verdaderas,
por segundo, unidad de ángulo sólido y unidad de volumen. Si suponemos que
estamos en condiciones de equilibrio
térmico, las poblaciones relativas de los dos niveles de energía
considerados verifican la ley de Boltzmann :
![]() , (10.13)
, (10.13)
en la cual T es la temperatura, ![]() y
y ![]() los pesos
estadísticos de los respectivos niveles y hn la diferencia de energía entre
los 2 niveles. En equilibrio térmico existe balance detallado de energía, de
manera que el número total de emisiones debe igualar el número de absorciones.
Esto es :
los pesos
estadísticos de los respectivos niveles y hn la diferencia de energía entre
los 2 niveles. En equilibrio térmico existe balance detallado de energía, de
manera que el número total de emisiones debe igualar el número de absorciones.
Esto es :
![]() ,
(10.14)
,
(10.14)
en la cual hemos usado ![]() en lugar de
en lugar de ![]() porque en condiciones
de equilibrio térmico la intensidad está dada por la función de Planck. De
(10.13) y (10.14) resulta :
porque en condiciones
de equilibrio térmico la intensidad está dada por la función de Planck. De
(10.13) y (10.14) resulta :
![]() ,
,
o bien, multiplicando por ![]() y ordenando términos, se tiene :
y ordenando términos, se tiene :
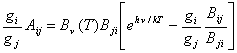 (10.15)
(10.15)
Reemplazando en (10.15) la función de Planck dada en (2.8) se obtiene :
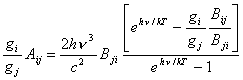 (10.16)
(10.16)
Dado que los 3 coeficientes de
Einstein que aparecen en esta última expresion no pueden depender de la
temperatura T, ya que son constantes
para un determinado átomo, deben entonces verificarse las siguientes igualdades
:
![]() (10.17)
(10.17)
y
![]() (10.18)
(10.18)
Nótese que si uno de los
coeficientes de Einstein se conoce, pueden derivarse los otros dos de las
expresiones anteriores. Por otra parte, si bien las relaciones entre los
coeficientes de Einstein han sido derivadas considerando condiciones de
equilibrio térmico, es importante destacar que las expresiones (10.17) y
(10.18) se mantienen en todas las condiciones.
El problema que nos planteamos en
este capítulo es obtener el coeficiente másico de absorción continua kn y hemos visto en la sección
precedente que las emisiones estimuladas o absorciones negativas tienen su
influencia en la absorción total. Si se escribe (10.12) de la siguiente manera
:
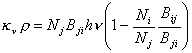 , (10.19)
, (10.19)
y se tienen en
cuenta (10.13) y (10.17) resulta :
![]() (10.20)
(10.20)
El término entre paréntesis en la expresión anterior tiene en cuenta las emisiones estimuladas, ya que
![]()
es pura absorción.
En rigor, lo que representa absorción verdadera es el producto
![]() .
.
Sin embargo, si se multiplica miembro a miembro la
expresión (10.20) por ![]() , el factor entre paréntesis representa las emisiones
estimuladas. En otras palabras, la absorción verdadera producida es disminuida
en un factor
, el factor entre paréntesis representa las emisiones
estimuladas. En otras palabras, la absorción verdadera producida es disminuida
en un factor ![]() , conocido como factor
de emisiones estimuladas, el cual aumenta a medida que aumenta la
temperatura y a medida que disminuye la frecuencia considerada. Para una
estrella A0V, por ejemplo, cuya temperatura superficial es del orden de 10.000 oK,
la disminución de la absorción debida al factor de emisiones estimuladas supera
el 20% en la región del continuo de Paschen y más allá de 10.000 Å sobrepasa el
30%.
, conocido como factor
de emisiones estimuladas, el cual aumenta a medida que aumenta la
temperatura y a medida que disminuye la frecuencia considerada. Para una
estrella A0V, por ejemplo, cuya temperatura superficial es del orden de 10.000 oK,
la disminución de la absorción debida al factor de emisiones estimuladas supera
el 20% en la región del continuo de Paschen y más allá de 10.000 Å sobrepasa el
30%.
Debe tenerse en cuenta que el factor
de emisiones estimuladas ha sido derivado para el caso de una transición
ligado-ligado. Milne (1924), sin embargo, ha mostrado que dicho factor se mantiene
para el caso de una transición libre-libre.