Na nossas derivações até o momento, usamos as condições de
contorno nulas, isto é 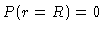 . Os modelos reais utilizam uma
condição um pouco mais realista, advinda dos modelos de atmosferas
estelares.
. Os modelos reais utilizam uma
condição um pouco mais realista, advinda dos modelos de atmosferas
estelares.
Quando discutimos transporte radiativo,
escrevemos a
equação de transporte radiativo
em um elemento com coeficiente de emissão jν:
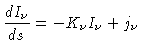 |
(1) |
onde ds é o elemento de distância (comprimento) com
coeficiente de absorção Kν,
atravessado pelo feixe de luz de intensidade específica Iν.
A profundidade ótica 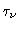 foi definida como
foi definida como
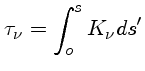 |
(2) |
de modo que
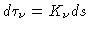 .
.
A função fonte 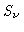 é definida pela equação
é definida pela equação
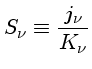 |
(3) |
Em equilíbrio termodinâmico local (ETL),
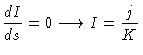 |
(4) |
e nenhuma radiação será transportada. Para
simplificar, estamos neste momento tratando do caso integrado em
freqüência e isotróprico. Como
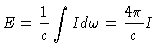 |
(5) |
Mas sabemos que em
equilíbrio termodinâmico local
(ETL)
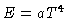 , logo
, logo
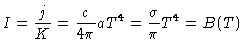 |
(6) |
isto é, em ETL
a função fonte é dada
pela função de Planck 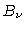 .
Se dividirmos a eq. (1) por
.
Se dividirmos a eq. (1) por 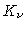 , podemos escrever
, podemos escrever
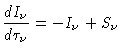 |
(7) |
ou
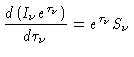 |
(8) |
que podemos integrar, obtendo
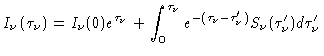 |
(9) |
Se a função fonte for independente da profundidade ótica,
Se houver equilíbrio termodinâmico local,
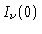 e
e 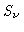 são iguais a
são iguais a
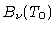 e
e 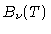 ,
onde
,
onde 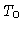 é a temperatura na camada onde
é a temperatura na camada onde 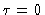 .
Para
.
Para 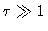 ,
,
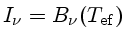 e
e
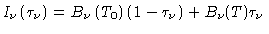 |
(12) |
O fluxo através da superfície da estrela, integrado
sobre todas as freqüências é dado por
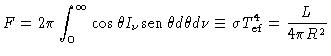 |
(13) |
Substituindo
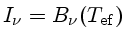 , obtemos
, obtemos
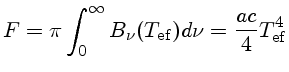 |
(14) |
Se considerarmos uma atmosfera plano-paralela e
assumirmos que o coeficiente de absorção 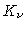 é independente da freqüência, podemos escrever
a equação de transporte radiativo como:
é independente da freqüência, podemos escrever
a equação de transporte radiativo como:
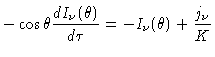 |
(15) |
onde 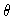 é o ângulo entre a normal e a direção considerada.
Integrando sobre freqüência,
é o ângulo entre a normal e a direção considerada.
Integrando sobre freqüência,
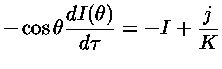 |
(16) |
Integrando-se agora a eq. (16) sobre o ângulo
sólido
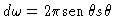 , e lembrando-se das
nossas definições:
, e lembrando-se das
nossas definições:
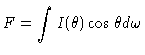 |
(18) |
e
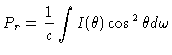 |
(19) |
podemos escrever
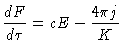 |
(20) |
Como em uma atmosfera estelar plana o fluxo é constante
(define-se uma atmosfera plana justamente para não
termos a variação de área de uma casca esférica),
esta equação
se reduz a
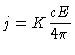 |
(21) |
Multiplicando-se a equação (16) por
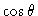 e integrando-se sobre o ângulo sólido, obtemos
e integrando-se sobre o ângulo sólido, obtemos
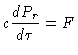 |
(22) |
e sua integral
Se assumirmos que 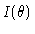 pode ser aproximado como
pode ser aproximado como
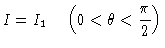 |
(24) |
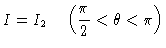 |
(25) |
isto é, o fluxo saindo da estrela é dado por 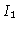 e o fluxo entrando
na estrela por
e o fluxo entrando
na estrela por 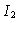 ,
podemos integrar as equações (17), (18) e (19) obtendo:
,
podemos integrar as equações (17), (18) e (19) obtendo:
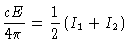 |
(26) |
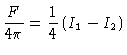 |
(27) |
e
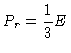 |
(28) |
Tendo em vista que não existe entrada de radiação pela atmosfera,
assumimos que 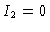 para
para 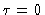 . Logo
. Logo 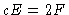 em
em 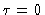 e a constante da equação (23) pode ser obtida:
Portanto
podemos escrever a equação (23) como
e a constante da equação (23) pode ser obtida:
Portanto
podemos escrever a equação (23) como
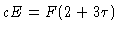 |
(29) |
Sabemos que nas condições de equilíbrio termodinâmico
local e assumindo 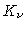 independente da freqüência,
a função fonte (eq. 3) é dada pela função
de Planck, e podemos escrever
independente da freqüência,
a função fonte (eq. 3) é dada pela função
de Planck, e podemos escrever
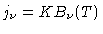 |
(30) |
onde 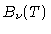 é a função de Planck.
Como
é a função de Planck.
Como
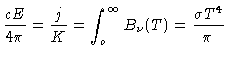 |
(31) |
podemos escrever eq. (29) como
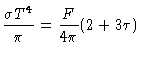 |
(32) |
e como o fluxo 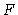 é dado por
é dado por
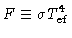 |
(33) |
A eq. (32) pode ser escrita como:
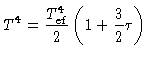 |
(34) |
demonstrando que a temperatura é igual à temperatura efetiva para
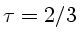 .
.
Da nossa definição de temperatura efetiva:
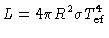 |
(35) |
e
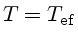 para uma profundidade ótica
para uma profundidade ótica 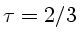 ,
podemos usar a equação de equilíbrio hidrostático
,
podemos usar a equação de equilíbrio hidrostático
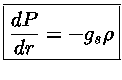 |
(36) |
e a definição de profundidade ótica
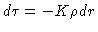 para escrever
para escrever
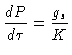 |
(37) |
e integrar
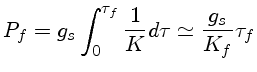 |
(38) |
e finalmente, substituindo
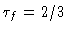 obter uma estimativa para a
pressão na fotosfera de
onde
obter uma estimativa para a
pressão na fotosfera de
onde 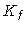 representa a opacidade na fotosfera.
Esta é a pressão na fotosfera, isto é, na mesma camada com
T=Tef.
representa a opacidade na fotosfera.
Esta é a pressão na fotosfera, isto é, na mesma camada com
T=Tef.



Próxima: Envelope Radiativo
Volta: Interiores Estelares
Anterior: Polítropos
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 7 set 2011
![]() . Os modelos reais utilizam uma
condição um pouco mais realista, advinda dos modelos de atmosferas
estelares.
. Os modelos reais utilizam uma
condição um pouco mais realista, advinda dos modelos de atmosferas
estelares.
![]() foi definida como
foi definida como
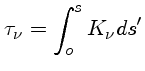
![]() é definida pela equação
é definida pela equação
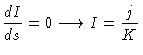
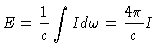
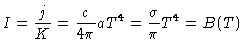
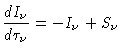
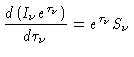
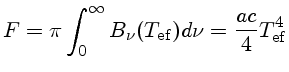
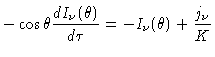
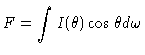
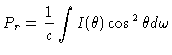
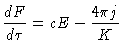
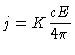
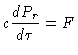
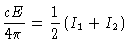
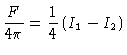
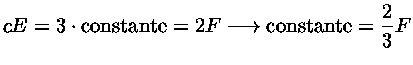
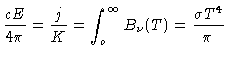
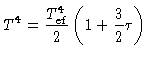
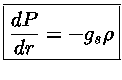
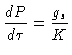
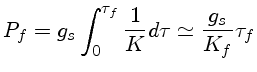
![]()