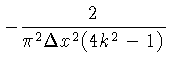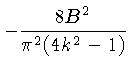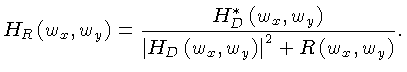


Próxima: Imagem SPECT
Volta: Transformadas de Fourier
Anterior: Retro-projeção
A reconstrução bi-dimensional por retro-projeção
filtrada é
o algoritmo mais utilizado em tomografia computadorizada
por transmissão e por emissão. Vamos aqui estudar o caso
de feixe paralelo, o mais simples. Da equação 4.31
e 4.34, podemos demonstrar que a função do objeto
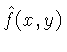 pode ser reconstruída dos dados de
projeção calculando-se:
pode ser reconstruída dos dados de
projeção calculando-se:
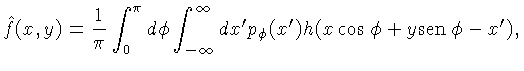 |
(4.35) |
onde 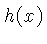 é a transformada inversa do Jacobiano
é a transformada inversa do Jacobiano 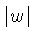 :
:
onde definimos um filtro 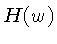 para substituir
para substituir 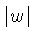 ,
já que a transformada inversa 4.36 não é
calculável devido a sua natureza divergente,
isto é, não satisfaz a condição de integrabilidade
(4.5):
,
já que a transformada inversa 4.36 não é
calculável devido a sua natureza divergente,
isto é, não satisfaz a condição de integrabilidade
(4.5):
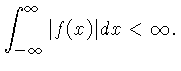 |
(4.38) |
A integral
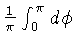 representa a retro-projeção, e
representa a retro-projeção, e 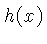 a filtragem.
a filtragem.
Os algoritmos de retro-projeção filtrada, substituem
a função 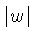 pelo filtro
pelo filtro 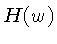 . Um filtro,
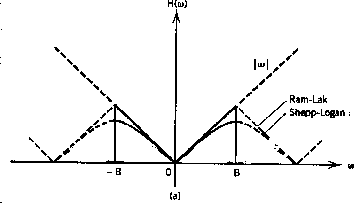
chamado de Ram-Lak, é apresentando na figura acima,
desenvolvido por Ramachandran e Lakshiminarayanan em 1971,
que assumem que a função
. Um filtro,
chamado de Ram-Lak, é apresentando na figura acima,
desenvolvido por Ramachandran e Lakshiminarayanan em 1971,
que assumem que a função 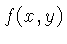 está
limitada na frequência espacial a
está
limitada na frequência espacial a 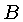 . Isto é
sempre verdade para imagens digitais, devido à amostragem
finita. Neste filtro, o kernel é definido por:
. Isto é
sempre verdade para imagens digitais, devido à amostragem
finita. Neste filtro, o kernel é definido por:
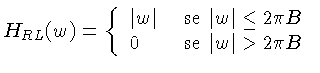 |
(4.39) |
O filtro no domínio espacial pode então ser obtido pela
transformada inversa de Fourier de 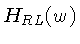 :
:
onde
é chamada de função erro.
Como os dados de projeção são discretos, o filtro também
deve ser discreto. Aplicando-se o critério de Nyquist, com dados uniformemente
espaçados por
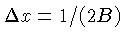 , o filtro de Ram-Lak para
posições discretas
, o filtro de Ram-Lak para
posições discretas
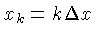 é dado por:
é dado por:
A borda acentuada do filtro Ram-Lak torna o filtro no domínio espacial
oscilatório e, portanto, introduz artefatos na imagem reconstruída.
Shepp e Logan, em 1974 sugeriram um filtro alternativo, introduzindo
um peso senoidal à função
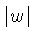 , efetivamente eliminando
estes artefatos.
, efetivamente eliminando
estes artefatos.
A função derivada é dada por:
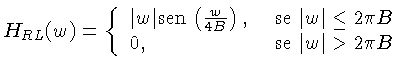 |
(4.46) |
O kernel do filtro no domínio espacial é dado por:
![$ h_{SL}(x) = \frac{B}{\pi^2}t\{ \frac{1-\cos 2\pi B[(1/4B)+x]}{(1/4B)+x} + \frac{1-\cos 2\pi B[(1/4B)-x]}{(1/4B)-x} \}$](img478.gif) |
(4.47) |
Substituindo-se
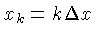 , obtemos a versão discreta:
, obtemos a versão discreta:
Estes filtros podem ainda ser generalizados
para feixes divergentes, e
levando-se em consideração
o ruído (filtros de Wiener).
Podemos escrever o filtro optimizado como:
onde
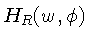 é o filtro de Wiener (4.16),
é o filtro de Wiener (4.16),
A reconstrução, tanto 2-D quanto 3-D,
portanto pode ser feita através da transformada de Fourier das
projeções, interpolando-se os dados de coordenadas polares
para coordenadas cartesianas, seguida da transformada inversa
bi- ou tri-dimensional, ou pelo algoritmo
de retro-projeção filtrada.
Note que os algoritmos de reconstrução na maioria dos
aparelhos assume que o feixe é monoenergético. Como o
coeficiente de atenuação linear é fortemente
dependente da energia, o uso de um coeficiente médio
é um fator de degradação de resolução.
Como feixes de raio-X de baixa energia são atenuados
mais fortemente que feixes de alta energia, pode-se
restringir a energia do feixe passando-o por um
filtro de alumínio ou cobre antes de passar
pelo paciente, tornando o feixe mais monoenergético.



Próxima: Imagem SPECT
Volta: Transformadas de Fourier
Anterior: Retro-projeção
©
Modificada em 21 set 1998
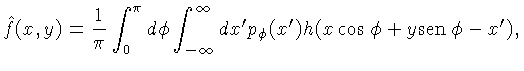
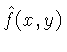 pode ser reconstruída dos dados de
projeção calculando-se:
pode ser reconstruída dos dados de
projeção calculando-se:
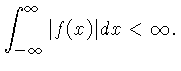
![]() representa a retro-projeção, e
representa a retro-projeção, e ![]() a filtragem.
a filtragem.
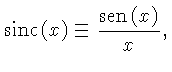
![]() , efetivamente eliminando
estes artefatos.
, efetivamente eliminando
estes artefatos.
![$ h_{SL}(x) = \frac{B}{\pi^2}t\{ \frac{1-\cos 2\pi B[(1/4B)+x]}{(1/4B)+x} + \frac{1-\cos 2\pi B[(1/4B)-x]}{(1/4B)-x} \}$](img478.gif)