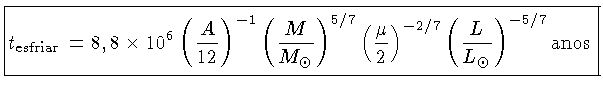Próxima: Cristalização
Volta: Anãs Brancas
Anterior: Evolução das Anãs Brancas
Ressaltamos que o calor específico de um gás de elétrons
degenerados é controlado pelos íons, pois os íons
têm a maior capacidade térmica no núcleo degenerado,
que contém praticamente toda a massa da estrela.
Produção de energia por reações nucleares e
por contração gravitacional contribuem muito pouco para
a luminosidade da estrela, se existem, e o núcleo é basicamente
isotérmico devido à alta eficiência da condução
térmica pelos elétrons degenerados.
Desta maneira, podemos modelar o núcleo como uma simples
fonte de calor, com a energia produzida pelo movimento térmico
dos íons.
Nestas condições, obteremos uma relação
do tipo lei de potência entre a idade e a luminosidade da estrela,
como encontrada por
Leon Mestel (1927-)
 em 1952:
em 1952:
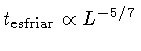
Seja 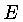 a
energia total armazenada pela anã branca; a luminosidade
será dada pela razão com que esta energia é irradiada:
a
energia total armazenada pela anã branca; a luminosidade
será dada pela razão com que esta energia é irradiada:
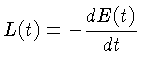
e define a taxa de esfriamento da anã branca.
Esta terminologia foi introduzida pelo reconhecimento
que a fonte da energia que é irradiada pela atmosfera
da estrela é a energia térmica da estrela (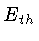 ).
Como a maior parte da anã branca é isotérmica,
a primeira aproximação é:
).
Como a maior parte da anã branca é isotérmica,
a primeira aproximação é:
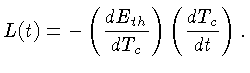
como mostraremos a seguir.
Nesta aproximação, os pequenos ajustes da densidade interna devido
ao esfriamento são desprezados, já que a energia gravitacional liberada
é completamente absorvida pelos elétrons degenerados, que são
forçados a níveis de energia mais altos.
Se processos nucleares (boa aproximação) e de emissão de neutrinos (má aproximação) são desprezados,
bem como a liberação de energia gravitacional residual
(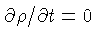 ),
a luminosidade da anã branca é diretamente proporcional
à taxa de decréscimo da temperatura da estrela.
),
a luminosidade da anã branca é diretamente proporcional
à taxa de decréscimo da temperatura da estrela.
Para um gás de elétrons degenerados mas não relativísticos,
a contribuição eletrônica para o calor específico
[seção (cve)],
por unidade de massa (Z elétrons por AH de massa),
derivada por Subrahmanyan Chandrasekhar (1910-1995)
(1939, An Introduction to the Study of
Stellar Structure, University of Chicago Press, p. 394),
é:
onde 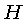 é a unidade de
massa atômica (
é a unidade de
massa atômica (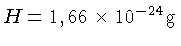 ),
Z é a carga média dos íons e
),
Z é a carga média dos íons e
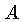 é o número atômico médio.
é o número atômico médio.
Como o gás está altamente degenerado, 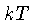 é muito
menor do que a energia de Fermi dos elétrons [eq. (1.4)],
é muito
menor do que a energia de Fermi dos elétrons [eq. (1.4)],
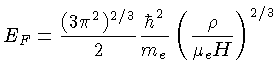 |
(1.80) |
e podemos desprezar 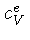 em comparação com o
calor específico dos íons.
Fisicamente, os elétrons não contribuem para o reservatório de
energia porque partículas degeneradas já ocupam seu estado de
energia mais baixo e, portanto, não podem esfriar.
Para um gás (de íons) ideal,
A equação básica de evolução estelar para
a conservação de energia é:
em comparação com o
calor específico dos íons.
Fisicamente, os elétrons não contribuem para o reservatório de
energia porque partículas degeneradas já ocupam seu estado de
energia mais baixo e, portanto, não podem esfriar.
Para um gás (de íons) ideal,
A equação básica de evolução estelar para
a conservação de energia é:
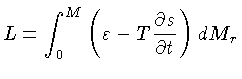 |
(1.81) |
O termo
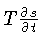 representa a troca de calor (perda)
por unidade de massa, e
representa a troca de calor (perda)
por unidade de massa, e
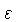 é a taxa de
geração ou perda de energia por unidade de massa
devido a reações nucleares ou emissão de neutrinos,
que desprezamos.
é a taxa de
geração ou perda de energia por unidade de massa
devido a reações nucleares ou emissão de neutrinos,
que desprezamos.
A alta degenerescência do núcleo da anã branca produz uma alta
eficiência de condução térmica pelos elétrons, tornando o
núcleo praticamente isotérmico.
Como
e desprezamos a variação da densidade, a equação (1.81) pode ser escrita como:
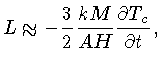 |
(1.82) |
onde 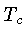 é a temperatura do núcleo.
é a temperatura do núcleo.
Para calcular 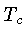 precisamos levar em conta a transferência de
energia pelo envelope fino e não degenerado. Se o envelope está
em equilíbrio radiativo, e pudermos utilizar a
lei de opacidade de Kramers:
precisamos levar em conta a transferência de
energia pelo envelope fino e não degenerado. Se o envelope está
em equilíbrio radiativo, e pudermos utilizar a
lei de opacidade de Kramers:
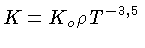 |
(1.83) |
levando-se conta as equações básicas:
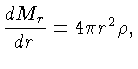
Continuidade da Massa
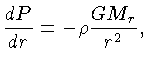
Equilíbrio Hidrostático
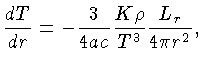
Equilíbrio Radiativo
podemos dividir a
equação do equilíbrio radiativo pela equação
do equilíbrio hidrostático, obtendo:
Tendo em vista que a base do envelope (He+H) ocorre a
aproximadamente 10-2M*,
podemos aproximar
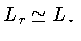 e
e
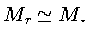 no envelope. Usando
podemos usar a lei de opacidade de Kramers (1.83) para obter:
que pode ser integrada usando-se a condição de contorno zero
para a superfície
(
no envelope. Usando
podemos usar a lei de opacidade de Kramers (1.83) para obter:
que pode ser integrada usando-se a condição de contorno zero
para a superfície
(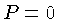 para
para 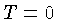 ), resultando em:
), resultando em:
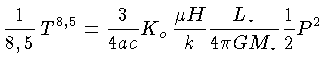 |
(1.84) |
onde 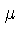 é o peso molecular médio no envelope
(
é o peso molecular médio no envelope
(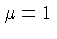 para hidrogênio e 2 para o hélio) e
para hidrogênio e 2 para o hélio) e 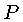 é a pressão.
é a pressão.
Na borda entre o núcleo isotérmico degenerado, a
pressão e a temperatura estão relacionados por
e obtemos
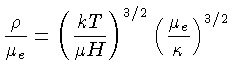 |
(1.85) |
e
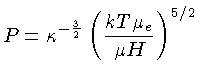 |
(1.86) |
Substituindo a expressão para a pressão
dada pela equação (1.86) na
equação (1.84), esta se reduz à relação entre
a luminosidade e a temperatura:
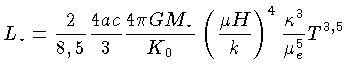 |
(1.87) |
e de (1.85)
podemos simplificar a equação (1.87) para:
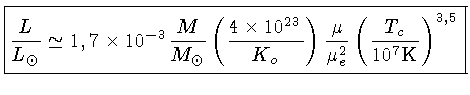 |
(1.88) |
onde
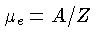 é o peso molecular médio por elétron
e
é o peso molecular médio por elétron
e 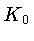 é o coeficiente da lei de Kramers
(1.83).
Esta é a razão que, no diagrama H-R, a sequência de esfriamento das anãs brancas
é uma reta (log L ∝ 3,5 log T).
é o coeficiente da lei de Kramers
(1.83).
Esta é a razão que, no diagrama H-R, a sequência de esfriamento das anãs brancas
é uma reta (log L ∝ 3,5 log T).
Podemos agora integrar a equação (1.82)
diretamente para obter a relação idade-luminosidade:
Esta é a lei de esfriamento de Mestel, na forma apresentada por
Hugh M. Van Horn (1938-).

As aproximações usadas para derivar a lei de Mestel foram:
- - Desprezar fontes e sumidouros de energia
(energia nuclear e esfriamento por neutrinos:
 ),
),
- - Desprezar contração gravitacional
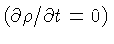 ,
,
- - Desprezar a capacidade térmica dos elétrons
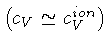 ,
,
- - Usar lei do gás perfeito para os íons
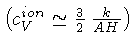 ,
,
- - Assumir que o núcleo é isotérmico
![$ [T(r) \equiv T_c]$](img707.gif) ,
,
- - Assumir equilíbrio radiativo no envelope,
- - Assumir uma lei de opacidade de Kramers no envelope.
Como a energia média de uma anã branca com
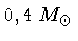 ,
,
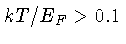 para
para
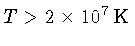 ,
não podemos desprezar o efeito de contração
gravitacional residual
para massas baixas. Também não podemos desprezar
a contribuição
eletrônica ao calor específico, já que
os elétrons podem contribuir com até 30-50% ao calor
específico de estrelas quentes, com núcleos de carbono.
E não podemos desprezar a perda de energia por neutrinos,
que pode ser dominante para Tef>30000 K,
dependendo da massa da estrela.
,
não podemos desprezar o efeito de contração
gravitacional residual
para massas baixas. Também não podemos desprezar
a contribuição
eletrônica ao calor específico, já que
os elétrons podem contribuir com até 30-50% ao calor
específico de estrelas quentes, com núcleos de carbono.
E não podemos desprezar a perda de energia por neutrinos,
que pode ser dominante para Tef>30000 K,
dependendo da massa da estrela.
Resultados mais precisos podem ser obtidos incluindo-se os
seguintes processos, desprezados na teoria de Mestel:
- esfriamento por neutrinos (
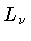 ),
importante para
),
importante para
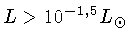 ;
;
- liberação de calor latente de cristalização,
importante para
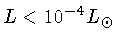 ;
;
- geração de energia nuclear pelo processo próton-próton
(
 ),
importante quando
),
importante quando
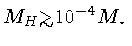 ;
;
- liberação de energia gravitacional para as camadas externas.
Uma fórmula aproximada que inclui estes efeitos é:
A dependência da luminosidade indica que as anãs brancas
mais quentes -- e mais luminosas --
esfriam mais rápido.
A idade das anãs brancas menos luminosas observadas
(com
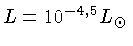 ) é cerca de
) é cerca de
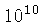 anos,
comparável com a idade das estrelas mais frias da nossa
Galáxia.
anos,
comparável com a idade das estrelas mais frias da nossa
Galáxia.
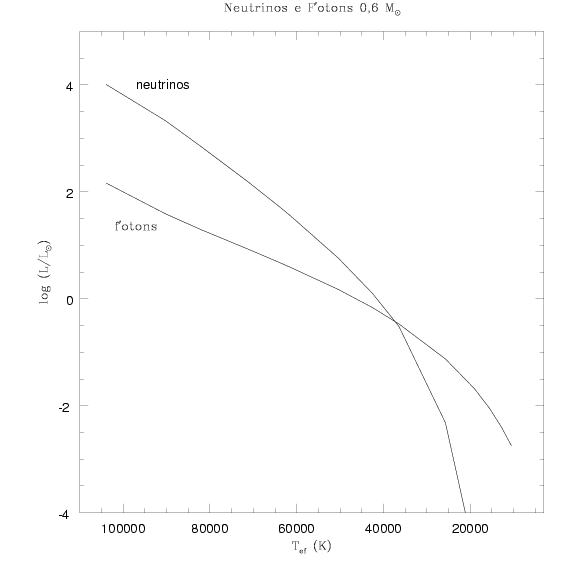
Evolução da luminosidade de uma anã
branca de 0,6 M
Sol com o tempo, representado pela
T
ef,
tanto de fótons quanto de neutrinos.
As anãs brancas mais frias também são dominadas pela
cristalização do núcleo e possível separação
total dos elementos no núcleo, e suas
camadas externas, embora de baixa densidade, também se tornam
degeneradas.
A idade total de uma anã branca depende não somente de seu esfriamento, mas de quanto
tempo levou a progenitora a chegar à fase de anã branca. Nos modelos de Alejandra
Romero de 2014, uma progenitora de uma massa solar
com z=0,0001, como a dos aglomerados globulares menos metálicos,
gera uma anã branca de 0,568 MSol em 5,9 Ganos,
enquanto uma com z=0,02, solar,
gera uma anã branca de 0,511 MSol em 12,5 Ganos.





Próxima: Cristalização
Volta: Anãs Brancas
Anterior: Evolução das Anãs Brancas
©
Modificada em 29 set 2014
 em 1952:
em 1952:
 em 1952:
em 1952:
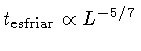
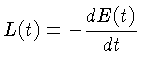
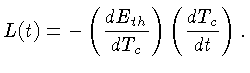
![]() ),
a luminosidade da anã branca é diretamente proporcional
à taxa de decréscimo da temperatura da estrela.
),
a luminosidade da anã branca é diretamente proporcional
à taxa de decréscimo da temperatura da estrela.
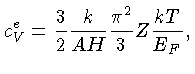
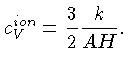
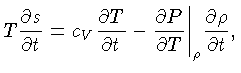
![]() precisamos levar em conta a transferência de
energia pelo envelope fino e não degenerado. Se o envelope está
em equilíbrio radiativo, e pudermos utilizar a
lei de opacidade de Kramers:
precisamos levar em conta a transferência de
energia pelo envelope fino e não degenerado. Se o envelope está
em equilíbrio radiativo, e pudermos utilizar a
lei de opacidade de Kramers:
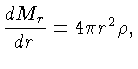 Continuidade da Massa
Continuidade da Massa
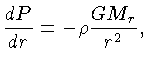 Equilíbrio Hidrostático
Equilíbrio Hidrostático
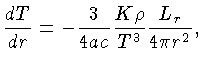 Equilíbrio Radiativo
Equilíbrio Radiativo
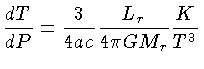
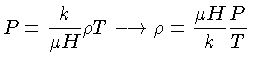
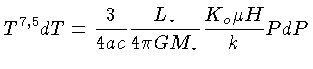
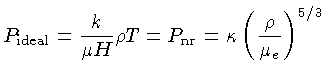
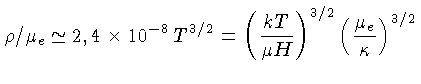
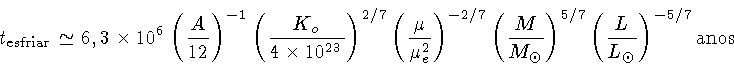

![]() ,
,
![]() para
para
![]() ,
não podemos desprezar o efeito de contração
gravitacional residual
para massas baixas. Também não podemos desprezar
a contribuição
eletrônica ao calor específico, já que
os elétrons podem contribuir com até 30-50% ao calor
específico de estrelas quentes, com núcleos de carbono.
E não podemos desprezar a perda de energia por neutrinos,
que pode ser dominante para Tef>30000 K,
dependendo da massa da estrela.
,
não podemos desprezar o efeito de contração
gravitacional residual
para massas baixas. Também não podemos desprezar
a contribuição
eletrônica ao calor específico, já que
os elétrons podem contribuir com até 30-50% ao calor
específico de estrelas quentes, com núcleos de carbono.
E não podemos desprezar a perda de energia por neutrinos,
que pode ser dominante para Tef>30000 K,
dependendo da massa da estrela.