Desde o início dos anos 1960, Aleksei Alexeevich Abrikosov (1928-2017) (1960, Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki, 39, 1798) ganhador do Nobel 2003 por supercondução, e David Abramovich Kirzhnits (1926-1998) (1960, Soviet Physics - Journal of Experimental and Theoretical Physics, 11, 365), na Rússia, e Edwin Ernest Salpeter (1925-2008) (1961, Astrophysical Journal, 134, 669) nos Estados Unidos, reconheceram independentemente que as interações Coulombianas, nas temperaturas relativamente baixas características das anãs brancas frias, forçam os íons a formar um sólido cristalino. A cristalização altera drasticamente o esfriamento das anãs brancas, devido à liberação do calor latente de cristalização e à mudança na capacidade térmica após a cristalização [Hugh M. Van Horn (1938-), 1968, Astrophysical Journal, 151, 227].
O parâmetro principal para a cristalização é
![]() ,
a razão entre a energia da interação de Coulomb
e a energia térmica:
,
a razão entre a energia da interação de Coulomb
e a energia térmica:
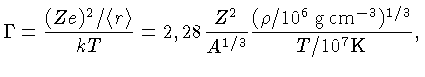
Quando Γ é pequeno, as interações Coulombianas são pequenas
e os íons formam um gás ideal, não interagente. Quando Γ≅1,
os íons sofrem interações de curto alcance e se comportam com
um fluido.
Nos modelos numéricos de Stephen George Brush (1935-), Harry L. Sahlin
(1935-1979) e
Edward Teller (1908-2003),
publicados em 1966 no Journal of Chemical Physics, 45, 2102, a transição
líquido-sólido ocorria para Γ≅126.
De acordo com os cálculos de 1978 de Carl John Hansen (1933-2011),
e de 1987 de Shuji Ogata e Setsuo Ichimaru, e outros, o início da
cristalização do carbono ocorre quando
![]() .
Nos modelos evolucionários de Matthew Allan Wood (1961-),
que podem ser obtidos de
http://faculty.tamuc.edu/mwood/wd.html,
com Γ=180,
o início da cristalização para uma anã branca
de 0,6
.
Nos modelos evolucionários de Matthew Allan Wood (1961-),
que podem ser obtidos de
http://faculty.tamuc.edu/mwood/wd.html,
com Γ=180,
o início da cristalização para uma anã branca
de 0,6 ![]() ocorre para Tef=6000 K se o núcleo for de
C (
ocorre para Tef=6000 K se o núcleo for de
C (![]() Gano,
Gano,
![]() ),
e para
Tef=7200 K se o núcleo for de O.
Os núcleos estarão a temperaturas de
),
e para
Tef=7200 K se o núcleo for de O.
Os núcleos estarão a temperaturas de
![]() K (carbono) e
K (carbono) e
![]() K (oxigênio).
Em 1991,
Kepler
de Souza Oliveira Filho
(1956-) e seus
colaboradores
Antonio Nemer Kanaan Neto (1966-),
Odilon Giovannini Jr. (1966-)
e Marcos Perez Diaz (1964-)
descobriram a anã branca variável
BPM 37093 = LTT 4816,
com massa de
K (oxigênio).
Em 1991,
Kepler
de Souza Oliveira Filho
(1956-) e seus
colaboradores
Antonio Nemer Kanaan Neto (1966-),
Odilon Giovannini Jr. (1966-)
e Marcos Perez Diaz (1964-)
descobriram a anã branca variável
BPM 37093 = LTT 4816,
com massa de
![]() e
e
![]() , e em 1998
demonstraram com os colaboradores do
Whole Earth Telescope que ela está
pelo menos 50% cristalizada.
Em 2005, Antonio Kanaan et al.,
"Whole Earth Telescope observations of BPM 37093:
A seismological test of crystallization theory in white dwarfs",
Astronomy & Astrophysics, 432, 219,
demonstraram que ela deve estar 90% cristalizada.
Em 2013,
James Joseph Hermes, S. O. Kepler, Barbara Garcia Castanheira, Alex Gianninas, Don Earl Winget, Michael Houston Montgomery, Warren R. Brown & Samuel T. Harrold,
no artigo Discovery of an Ultramassive Pulsating White Dwarf, publicado no
Astrophysical Journal Letters, 771, L2,
relatam a descoberta de uma anã branca pulsante com 1,20±0,03 MSol e Tef=12030±210 K,
que portanto deve estar ainda mais cristalizada do que a BPM 37093.
, e em 1998
demonstraram com os colaboradores do
Whole Earth Telescope que ela está
pelo menos 50% cristalizada.
Em 2005, Antonio Kanaan et al.,
"Whole Earth Telescope observations of BPM 37093:
A seismological test of crystallization theory in white dwarfs",
Astronomy & Astrophysics, 432, 219,
demonstraram que ela deve estar 90% cristalizada.
Em 2013,
James Joseph Hermes, S. O. Kepler, Barbara Garcia Castanheira, Alex Gianninas, Don Earl Winget, Michael Houston Montgomery, Warren R. Brown & Samuel T. Harrold,
no artigo Discovery of an Ultramassive Pulsating White Dwarf, publicado no
Astrophysical Journal Letters, 771, L2,
relatam a descoberta de uma anã branca pulsante com 1,20±0,03 MSol e Tef=12030±210 K,
que portanto deve estar ainda mais cristalizada do que a BPM 37093.
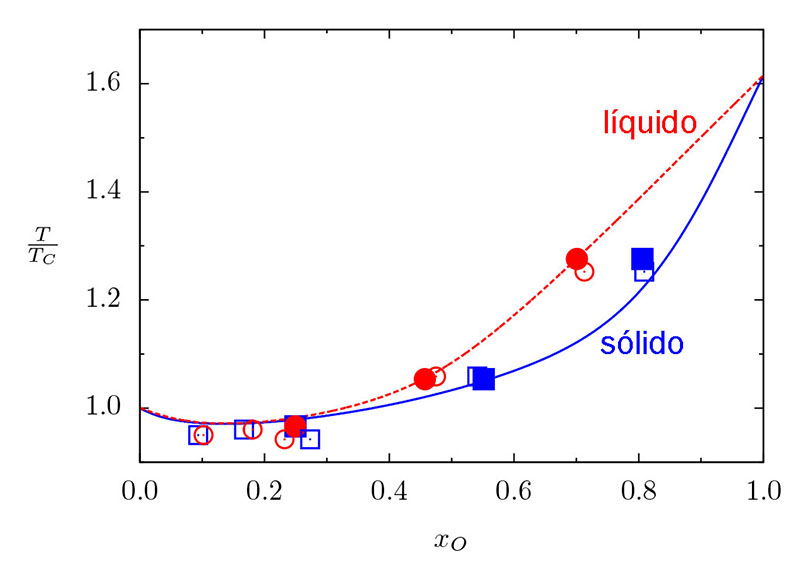
Em 2010, Charles J. Horowitz, Andre S. Schneider & Don K Berry publicaram no Physical Review Letters, 104, 1101 um estudo do diagrama de fase da cristalização de mistura de carbono e oxigênio, demonstrando que a cristalização da mistura ocorre em temperatura cerca de 1,23× mais baixa do que carbono puro, já que as impurezas dificultam a cristalização, levando a Γ=ECoulomb/Etérmica≅ 220. Os mesmos resultados foram encontrados por Zach Medin & Andrew Cummingem 2010, Physical Review E, 81, 036107. Alejandra Daniela Romero, S.O. Kepler, Alejandro Hugo Córsico, Leandro Gabriel Althaus & Luciano Fraga, no artigo de 2013, Asteroseismological Study of Massive ZZ Ceti Stars with Fully Evolutionary Models, publicado no Astrophysical Journal, 779, 58, demonstraram que os dados sismológicos são consistentes com Γ=220, consistentes com a mistura de carbono e oxigênio no núcleo predita pelos modelos.
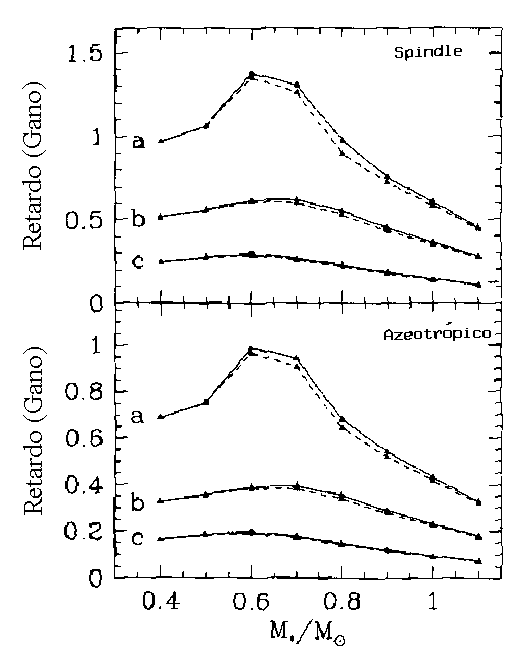
A cristalização da estrela, além de alterar o calor específico dos íons, pode levar à separação de fase, isto é, à deposição do oxigênio para o centro, formando cristais separados de carbono e oxigênio, dependendo de como for a transição de fase: tipo spindle, azeotrópica ou eutética. Como a cristalização nas condições de pressão e temperatura do interior das anãs brancas não pode ser testada em laboratório, é preciso calculá-la. Mas os efeitos quânticos são importantes. Gilles Chabrier, Neil W. Ashcroft e Hugh W. DeWitt (1992), Nature, 360, 48, calcularam a energia de interação entre os íons e demonstraram que E0/kT >2 após a transição de fase, isto é, os cristais no interior das anãs brancas são cristais quânticos.
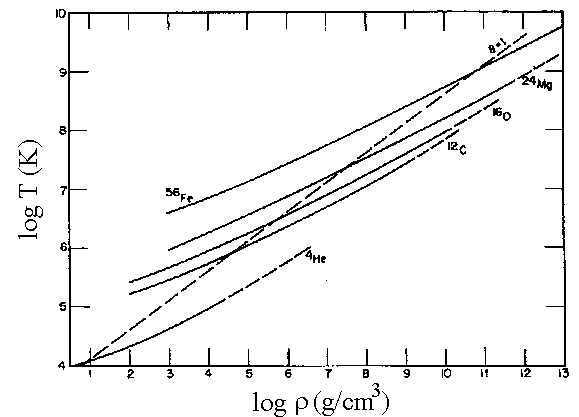
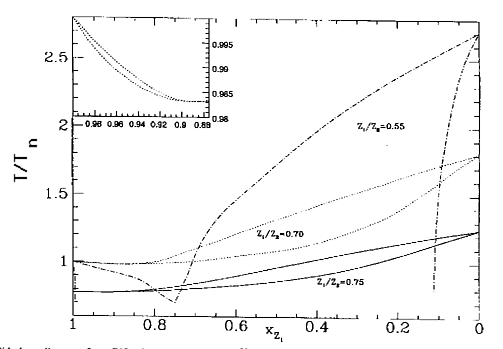
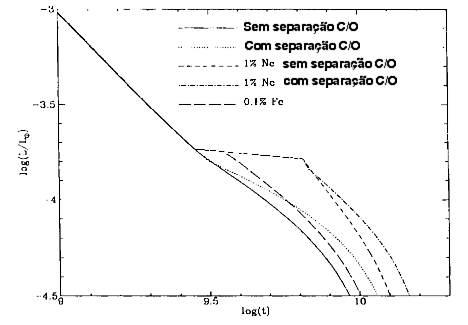


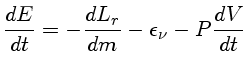
Se a anã branca é composta de dois elementos químicos, por
exemplo C e O, de modo que
![]() , podemos reescrever
esta equação como:
, podemos reescrever
esta equação como:
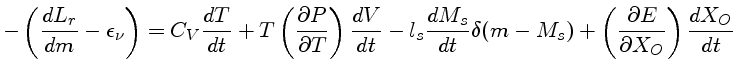
Durante a cristalização, o calor latente de fusão
![]() ,
correspondendo a ΔE≅2×1046ergs
para uma anã branca de 0,6 MSol,
é liberado, aumentando
o tempo de esfriamento em
30%, acima do valor calculado pela
teoria de Mestel.
Para esta anã branca de 0,6 MSol,
isto ocorre quando L=10-4,5LSol,
e corresponde a Δt≅1,8 Ganos
(Leandro Gabriel Althaus et al. 2010, Astronomy &
Astrophysics Review).
Ao cristalizar, o calor específico dos íons
,
correspondendo a ΔE≅2×1046ergs
para uma anã branca de 0,6 MSol,
é liberado, aumentando
o tempo de esfriamento em
30%, acima do valor calculado pela
teoria de Mestel.
Para esta anã branca de 0,6 MSol,
isto ocorre quando L=10-4,5LSol,
e corresponde a Δt≅1,8 Ganos
(Leandro Gabriel Althaus et al. 2010, Astronomy &
Astrophysics Review).
Ao cristalizar, o calor específico dos íons
![]() aumenta de
aumenta de
![]() para
para
![]() ,
de modo que o tempo de vida da anã branca aumenta
por uma fator de dois, até que o núcleo atinja a
temperatura de Debye [Peter Debye (1884-1966)].
,
de modo que o tempo de vida da anã branca aumenta
por uma fator de dois, até que o núcleo atinja a
temperatura de Debye [Peter Debye (1884-1966)].
A temperatura de Debye (![]() ), é definida como
), é definida como
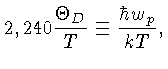
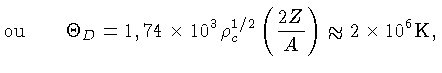
![w_p^2 = \frac{4\pi n_e e^2}{m_e}[1+(\frac{\hbar}{m_e c})^2
(3\pi^2 n_e)^{2/3}]^{-\frac{1}{2}}$](wpd.gif)
| Tef | Idade | log Pc | log Tc | log |
log R | log L/LSol | log Lneut/LSol | Mcrist/M* | |
|---|---|---|---|---|---|---|---|---|---|
| 101274 K | 245 000 anos | 24,597 | 8,0126 | 7,4730 | 8,8369 | 0,9577 | 1,9617 | 0,000 | 12,6 |
| 45973 K | 4,12 Manos | 24,637 | 7,8034 | 7,5020 | 8,7804 | -0,5276 | -0,3276 | 0,000 | 20,8 |
| 23686 K | 146 Manos | 24,660 | 7,2794 | 7,5192 | 8,7603 | -1,7197 | -4,3327 | 0,000 | 70,4 |
| 14849 K | 538 Manos | 24,665 | 6,9477 | 7,5234 | 8,7529 | -2,5458 | -6,2979 | 0,016 | 151,6 |
| 12255 K | 1,026 Ganos | 24,667 | 6,8036 | 7,5246 | 8,7509 | -2,8833 | -7,1046 | 0,396 | 211,4 |
| 10130 K | 1,740 Ganos | 24,668 | 6,6585 | 7,5255 | 8,7489 | -3,2575 | -10 | 0,748 | 295,5 |
| 6627 K | 3,908 Ganos | 24,669 | 6,3525 | 7,5263 | 8,7458 | -3,9616 | -10 | 0,945 | 598,2 |
| 4733 K | 6,845 Ganos | 24,670 | 5,8726 | 7,5265 | 8,7430 | -4,5519 | -10 | 0,970 | 1806,1 |
| 3369 K | 7,732 Ganos | 24,670 | 5,4889 | 7,5266 | 8,7425 | -5,1436 | -10 | 1,000 | 4369,8 |
| Tef | Idade | log Pc | log Tc | log |
log R | log L/LSol | log Lneut/LSol | Mcrist/M* | |
|---|---|---|---|---|---|---|---|---|---|
| 103992 K | 18 316 anos | 22,829 | 8,1742 | 6,2590 | 9,4167 | 2,1631 | 1,8449 | 0,000 | 3,4 |
| 46281 K | 2,65 Manos | 23,191 | 7,8279 | 6,5050 | 9,0392 | 0,0016 | 0,4282 | 0,000 | 9,1 |
| 23856 K | 29,54 Manos | 23,242 | 7,5792 | 6,5410 | 8,9817 | -1,2646 | -1,5832 | 0,000 | 16,7 |
| 12114 K | 368,44 Manos | 23,264 | 7,0568 | 6,5569 | 8,9557 | -2,4936 | -6,3225 | 0,000 | 56,1 |
| 10012 K | 604,97 Manos | 23,267 | 6,9198 | 6,5587 | 8,9513 | -2,8335 | -10 | 0 | 77,1 |
| 6647 K | 1,767 Ganos | 23,270 | 6,6244 | 6,5611 | 8,9426 | -3,5622 | -10 | 0,022 | 152,5 |
| 4554 K | 6,540 Ganos | 23,273 | 6,1452 | 6,5629 | 8,9340 | -4,2366 | -10 | 0,933 | 460,1 |
| 4044 K | 7,799 Ganos | 23,273 | 5,9823 | 6,5631 | 8,9332 | -4,4448 | -10 | 1,000 | 669,8 |
| 3304 K | 9,373 Ganos | 23,273 | 5,7627 | 6,5632 | 8,9324 | -4,7976 | -10 | 1,000 | 1110,6 |
