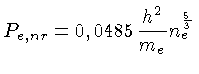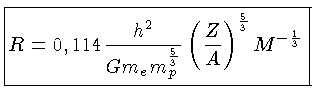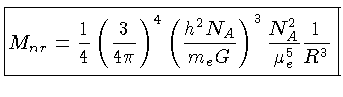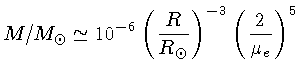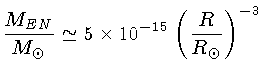Próxima: Massa de Chandrasekhar
Volta: Anãs Brancas
Anterior: Anãs Brancas
A análise das isócronas das sequências principais dos cúmulos
abertos que contém anãs brancas sugere que as anãs brancas --
não associadas a estrelas binárias --
têm progenitores com massas entre
0,8 e 10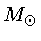 . As anãs brancas têm temperaturas desde
200 000 K até 3700 K e luminosidades correspondentes entre
. As anãs brancas têm temperaturas desde
200 000 K até 3700 K e luminosidades correspondentes entre
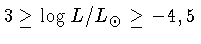 .
.
Apesar de suas origens diversas e suas diferentes luminosidades, as anãs
brancas formam uma classe bastante homogênea. Depois da fase
de pré-anãs brancas, as anãs brancas não binárias têm
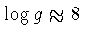 (cgs), correspondente a uma distribuição de massa
bastante restrita, centrada em
(cgs), correspondente a uma distribuição de massa
bastante restrita, centrada em 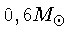 , mas são conhecidas anãs brancas com log g=5,5 (no sistema cgs, equivalente a uma massa de 0,05 MSol) a 10 (massa=1,36 MSol).
Hoje em dia, cerca de 30 000 anãs-brancas são conhecidas.
, mas são conhecidas anãs brancas com log g=5,5 (no sistema cgs, equivalente a uma massa de 0,05 MSol) a 10 (massa=1,36 MSol).
Hoje em dia, cerca de 30 000 anãs-brancas são conhecidas.
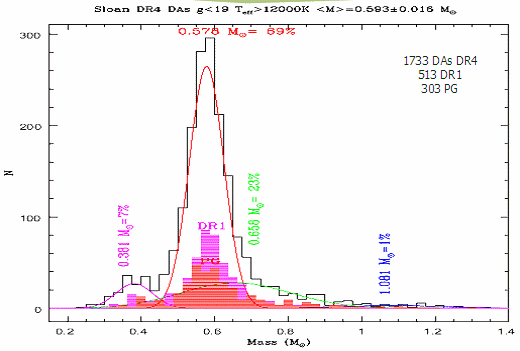 Kepler de Souza Oliveira Filho (1956-), Scot J. Kleinman, Atsuko Nitta, Detlev Koester (1941-), Bárbara Garcia Castanheira (1979-),
Odilon Giovannini, Alex Fabiano Murillo da Costa e Leandro Gabriel Althaus (1965-),
publicaram em 2007, o artigo
White dwarf mass distribution in the SDSS, no
Monthly Notices of the Royal Astronomical Society 375 (4), 1315,
onde determinaram a distribuição de massa das anãs brancas DAs.
Scot J. Kleinman, S. O. Kepler, Detlev Koester, Ingrid Pelisoli, Viviane Peçanha, Atsuko Nitta,
José Eduardo da Silveira Costa, Jurek Krzesinski, Patrick Dufour, François-René Lachapelle, Pierre Bergeron, Ching-Wa Yip, Hugh C. Harris, Daniel J. Eisenstein, Leandro Gabriel Althaus, Alejandro Hugo Córsico publicaram o
SDSS DR7 White Dwarf Catalog,
em 2013, no Astrophysical Journal Supplement Series, 204, 5-19, com 19 712 anãs brancas.
Kepler de Souza Oliveira Filho (1956-), Scot J. Kleinman, Atsuko Nitta, Detlev Koester (1941-), Bárbara Garcia Castanheira (1979-),
Odilon Giovannini, Alex Fabiano Murillo da Costa e Leandro Gabriel Althaus (1965-),
publicaram em 2007, o artigo
White dwarf mass distribution in the SDSS, no
Monthly Notices of the Royal Astronomical Society 375 (4), 1315,
onde determinaram a distribuição de massa das anãs brancas DAs.
Scot J. Kleinman, S. O. Kepler, Detlev Koester, Ingrid Pelisoli, Viviane Peçanha, Atsuko Nitta,
José Eduardo da Silveira Costa, Jurek Krzesinski, Patrick Dufour, François-René Lachapelle, Pierre Bergeron, Ching-Wa Yip, Hugh C. Harris, Daniel J. Eisenstein, Leandro Gabriel Althaus, Alejandro Hugo Córsico publicaram o
SDSS DR7 White Dwarf Catalog,
em 2013, no Astrophysical Journal Supplement Series, 204, 5-19, com 19 712 anãs brancas.
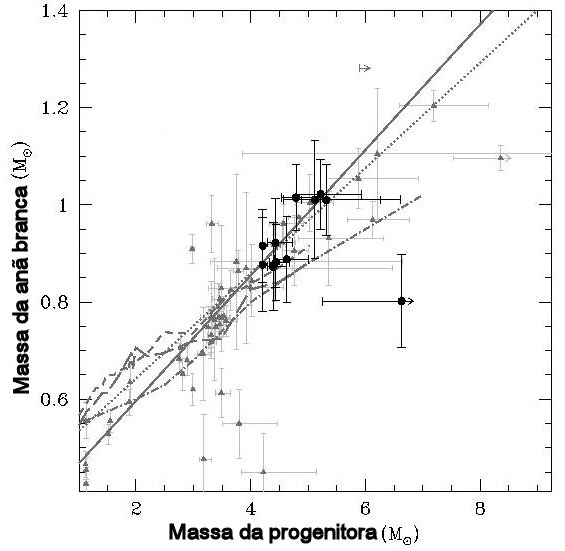
Relação massa inicial vs massa final para as estrelas que dão origem
às anãs brancas, publicada por
Kurtis A.
Williams, Michael Bolte e Detlev Koester
2009, Astrophysical Journal, 693, 355
encontram
Mfinal=(0.129± 0.004)Minicial +(0.339 ± 0.015)MSol
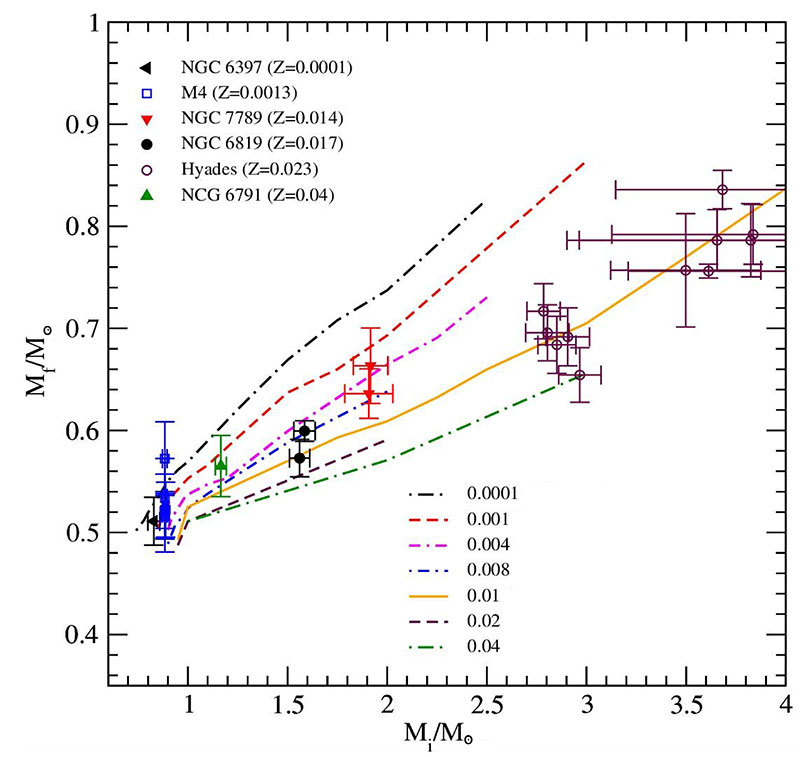
Dependência da relação massa inicial vs. massa final com a metalicidade
calculada por Alejandra Romero em 2014, indicada por z na figura.
É importante ressaltar que as idades dos modelos de mesma massa inicial
mas vindo de progenitores com
metalicidades diferentes, chegam a ter 5 Ganos de diferença, por
diferenças na vida pré-anã branca.
Uma progenitora de uma massa solar
com z=0,0001, como a dos aglomerados globulares menos metálicos,
gera uma anã branca de 0,568 MSol em 5,9 Ganos,
enquanto uma com z=0,02, solar,
gera uma anã branca de 0,511 MSol em 12,5 Ganos.
É importante notar que os núcleos das nebulosas planetárias
observadas em nossa
galáxia também têm massa centrada em
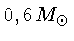 , embora exista um fator de seleção
em favor dos núcleos de
nebulosas planetárias com esta massa.
, embora exista um fator de seleção
em favor dos núcleos de
nebulosas planetárias com esta massa.
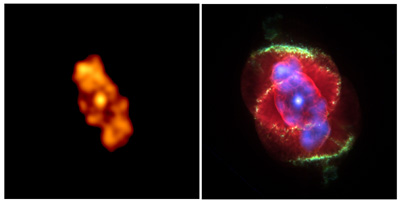
A esquerda vemos uma imagem obtida em raio-X pelo observatório Chandra,
do núcleo da nebulosa planetária "Olho de Gato", mostrada a direita.
Na imagem do Chandra vemos uma nuvem de milhões de graus envolvendo
o núcleo.
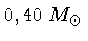 têm
vida na sequência principal maior do que a idade da nossa galáxia,
de modo que as anãs brancas com estas massas devem ser oriundas
da evolução de sistemas binários.
Da mesma forma, a teoria de evolução estelar prediz que
a massa mínima para a ignição do hélio nuclear
é de 0,45 a 0,47 MSol,
sugerindo que estas estrelas
têm núcleo de hélio
(Don A. VandenBerg, P.A. Bergbusch & P.D. Dowler, 2006,
Astrophysical Journal Supplement, 162, 375; Jorge Alejandro
Panei, Leandro Gabriel Althaus, X. Chen, & Zhanwen Han, 2007,
Monthly Notices of the Royal Astronomical Society,
382, 779).
Lee Anne Willson,
em seu artigo de 2000 no Annual Review of
Astronomy and Astrophysics, 38, 573,
propõe que, como as estrelas de baixa metalicidade têm
menor perda de massa, seus núcleos crescem até
cerca de 1 massa solar,
antes do envelope decrescer para
0,02 da massa da estrela, quando a estrela sai do ramo assimptótico das
supergigantes e, portanto, as estrelas de baixa metalicidade
formariam anãs brancas de mais alta massa.
têm
vida na sequência principal maior do que a idade da nossa galáxia,
de modo que as anãs brancas com estas massas devem ser oriundas
da evolução de sistemas binários.
Da mesma forma, a teoria de evolução estelar prediz que
a massa mínima para a ignição do hélio nuclear
é de 0,45 a 0,47 MSol,
sugerindo que estas estrelas
têm núcleo de hélio
(Don A. VandenBerg, P.A. Bergbusch & P.D. Dowler, 2006,
Astrophysical Journal Supplement, 162, 375; Jorge Alejandro
Panei, Leandro Gabriel Althaus, X. Chen, & Zhanwen Han, 2007,
Monthly Notices of the Royal Astronomical Society,
382, 779).
Lee Anne Willson,
em seu artigo de 2000 no Annual Review of
Astronomy and Astrophysics, 38, 573,
propõe que, como as estrelas de baixa metalicidade têm
menor perda de massa, seus núcleos crescem até
cerca de 1 massa solar,
antes do envelope decrescer para
0,02 da massa da estrela, quando a estrela sai do ramo assimptótico das
supergigantes e, portanto, as estrelas de baixa metalicidade
formariam anãs brancas de mais alta massa.
Podemos calcular a relação entre a massa de uma
anã branca e seu raio, usando a expressão
para a pressão de um gás totalmente degenerado mas não relativístico
[eq. (1.14)]:
na equação de equilíbrio hidrostático; obtém-se
(veja derivação em polítropos)
ou
onde 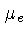 é o peso molecular médio dos elétrons, e é
igual a 2 para He, C, ou O totalmente ionizados.
Numericamente
Como a maioria das anãs brancas tem massa de
é o peso molecular médio dos elétrons, e é
igual a 2 para He, C, ou O totalmente ionizados.
Numericamente
Como a maioria das anãs brancas tem massa de
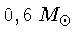 ,
obtemos um raio de R=6380 km.
Entretanto esta fórmula só é valida
para material completamente degenerado, o que não é o caso abaixo de
1,3 massas solares. O raio de uma anã branca de
,
obtemos um raio de R=6380 km.
Entretanto esta fórmula só é valida
para material completamente degenerado, o que não é o caso abaixo de
1,3 massas solares. O raio de uma anã branca de
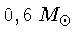 varia de cerca de 11 000 km para Tef=60 000 K,
para 8600 km para Tef=4 000 K.
Note que o raio diminui para massa maior.
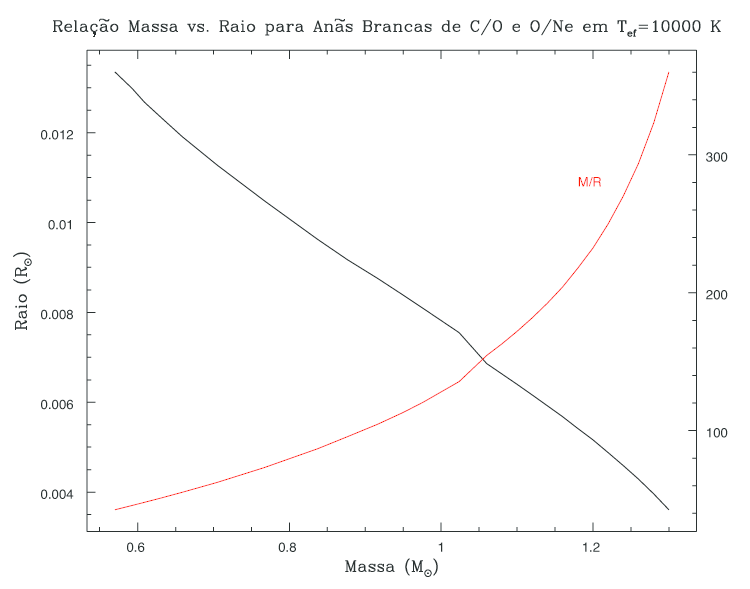
Nos modelos evolucionários, o raio de uma anã branca
com 1,2MSol de 15 000K, é 3975 km se o núcleo
for de C, 3902 km se de O e 3624 km se de O/Ne.
Se substituirmos
varia de cerca de 11 000 km para Tef=60 000 K,
para 8600 km para Tef=4 000 K.
Note que o raio diminui para massa maior.
Nos modelos evolucionários, o raio de uma anã branca
com 1,2MSol de 15 000K, é 3975 km se o núcleo
for de C, 3902 km se de O e 3624 km se de O/Ne.
Se substituirmos
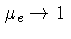 e
e
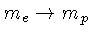 ,
podemos estimar a relação entre a massa e o raio para
uma estrela de nêutrons, já que neste caso, são os nêutrons
que estão degenerados:
que resulta em um raio de 11 km para uma massa de uma massa solar.
As estrelas de nêutrons têm massa média de
,
podemos estimar a relação entre a massa e o raio para
uma estrela de nêutrons, já que neste caso, são os nêutrons
que estão degenerados:
que resulta em um raio de 11 km para uma massa de uma massa solar.
As estrelas de nêutrons têm massa média de
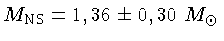 .
.
 Astronomia e Astrofísica
Astronomia e Astrofísica






Próxima: Massa de Chandrasekhar
Volta: Anãs Brancas
Anterior: Anãs Brancas
©
Modificada em 11 jul 2016
![]() . As anãs brancas têm temperaturas desde
200 000 K até 3700 K e luminosidades correspondentes entre
. As anãs brancas têm temperaturas desde
200 000 K até 3700 K e luminosidades correspondentes entre
![]() .
.
![]() (cgs), correspondente a uma distribuição de massa
bastante restrita, centrada em
(cgs), correspondente a uma distribuição de massa
bastante restrita, centrada em ![]() , mas são conhecidas anãs brancas com log g=5,5 (no sistema cgs, equivalente a uma massa de 0,05 MSol) a 10 (massa=1,36 MSol).
Hoje em dia, cerca de 30 000 anãs-brancas são conhecidas.
, mas são conhecidas anãs brancas com log g=5,5 (no sistema cgs, equivalente a uma massa de 0,05 MSol) a 10 (massa=1,36 MSol).
Hoje em dia, cerca de 30 000 anãs-brancas são conhecidas.