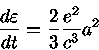Aceleração de Larmor
Se uma carga  está em repouso, o campo elétrico produzido será
radial,
está em repouso, o campo elétrico produzido será
radial,  . Se a carga for acelerada para uma pequena velocidade
. Se a carga for acelerada para uma pequena velocidade
 em um
em um  , depois
de um tempo
, depois
de um tempo  haverá um campo elétrico perpendicular ao movimento:
onde
haverá um campo elétrico perpendicular ao movimento:
onde  é o ângulo entre o vetor de aceleração e observador.
é o ângulo entre o vetor de aceleração e observador.
Pela Lei de Coulomb, no sistema c.g.s, o campo (força) elétrico é dado por:
Substituindo  , obtemos
A energia irradiada por unidade de área
(erg/s/cm2),
o fluxo de Poynting [John Henry Poynting (1852-1914)]
e como
, obtemos
A energia irradiada por unidade de área
(erg/s/cm2),
o fluxo de Poynting [John Henry Poynting (1852-1914)]
e como  ,
ou, com a aceleração
,
ou, com a aceleração
 ,
A potência emitida é obtida integrando-se sobre todas as direções
e como
,
A potência emitida é obtida integrando-se sobre todas as direções
e como
 ,
Espalhamento de Thompson
,
Espalhamento de Thompson