Recapitulando, com
as quatro equações de equilíbrio e as equações
da física da matéria,
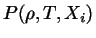 ,
,
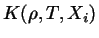 e
e
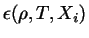 ,
além da condição de equilíbrio radiativo
,
além da condição de equilíbrio radiativo
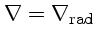
se
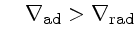
ou convectivo
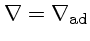
se
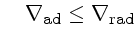
ou seja, o gradiente real é o menor dos dois, e as condições de contorno, podemos calcular a estrutura
estelar.
Uma dificuldade é que as condições de contorno estão separadas: um par
se refere ao centro e outro par se refere à superfície.
E nem sempre existe uma solução em equilíbrio
para certas escolhas de massa total e composição química.
Uma maneira de resolver o sistema de equações é usando o
método de integração chamado de Runge-Kutta
[Carl David Tolmé Runge (1856-1927) e Wilhelm Martin Kutta (1867 - 1944)],
que envolve
o cálculo de uma série de derivadas da variável
dependente, 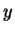 , em uma série de pontos no intervalo começando
em
, em uma série de pontos no intervalo começando
em 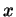 e terminando em
e terminando em 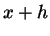 , onde
, onde 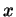 é a variável independente
e
é a variável independente
e 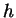 é chamado de passo. Estas derivadas são então utilizadas
para encontrar
é chamado de passo. Estas derivadas são então utilizadas
para encontrar 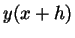 . As versões mais sofisticadas do método
automaticamente ajustam o valor do passo para manter a precisão
desejada.
. As versões mais sofisticadas do método
automaticamente ajustam o valor do passo para manter a precisão
desejada.
Outro método, usado no cálculo de modelos estelares reais, leva
em conta que, se integrarmos do centro para fora, é possível
que pequenos erros no núcleo sejam amplificados ao chegar na
superfície, como a idéia de balançar amplamente
a ponta de um chicote com pequenos movimentos de mão.
O mesmo problema acontece nos modelos estelares devido ao
grande contraste entre as condições centrais e superficiais,
e a condição de equilíbrio radiativo contém o fator T-4,
enquanto a condição de equilíbrio hidrostático depende de r-4.
O método usado é integrar a partir do centro e da superfície
simultaneamente e ver se as soluções se ajustam de
forma contínua em algum ponto entre os extremos,
por exemplo na borda entre o núcleo convectivo e
o envelope radiativo, nas estrelas de alta massa.
Precisamos então minimizar
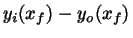 , onde
, onde 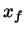 é o ponto de ajuste, de modo que podemos calcular a derivada
desta diferença, que deve se anular no ponto de mínimo.
Como nossas funções não são lineares, iteramos o
cálculo até que a diferença esteja dentro da precisão
pré-determinada. Este método, de transformar um problema
não linear em um linear, chama-se de método de
Newton-Raphson
[Isaac Newton (1642-1727) e Joseph Raphson (1648-1715)].
No método de Henyey, a cada iteração correções para todas as
variáveis em todos os pontos são calculados simultaneamente
[Louis George Henyey (1910-1970),
J.E. Forbes e Nancy L. Gould 1964, Astrophysical Journal, 139, 306].
Nosso cálculo para estrelas esféricas consiste então em um sistema
de 4 equações diferenciais ordinárias para as 4 variáveis: r, P, T e L.
Como linearizamos as equações assumindo correções pequenas,
se a aproximação inicial é muito diferente da solução,
as correções necessárias são grandes e o sistema não converge.
é o ponto de ajuste, de modo que podemos calcular a derivada
desta diferença, que deve se anular no ponto de mínimo.
Como nossas funções não são lineares, iteramos o
cálculo até que a diferença esteja dentro da precisão
pré-determinada. Este método, de transformar um problema
não linear em um linear, chama-se de método de
Newton-Raphson
[Isaac Newton (1642-1727) e Joseph Raphson (1648-1715)].
No método de Henyey, a cada iteração correções para todas as
variáveis em todos os pontos são calculados simultaneamente
[Louis George Henyey (1910-1970),
J.E. Forbes e Nancy L. Gould 1964, Astrophysical Journal, 139, 306].
Nosso cálculo para estrelas esféricas consiste então em um sistema
de 4 equações diferenciais ordinárias para as 4 variáveis: r, P, T e L.
Como linearizamos as equações assumindo correções pequenas,
se a aproximação inicial é muito diferente da solução,
as correções necessárias são grandes e o sistema não converge.
No cálculo de uma seqüência evolucionária, isto é, como
um modelo de certa massa evolui com o tempo, podemos empregar um
método explícito de cálculo, em que o estado de um sistema
em um tempo
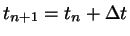 só depende do conhecimento
do estado em tempo
só depende do conhecimento
do estado em tempo  . Este método assume que os movimentos
são subsônicos, isto é, que choques não se desenvolvem.
. Este método assume que os movimentos
são subsônicos, isto é, que choques não se desenvolvem.
Se choques se desenvolvem, como por
exemplo em supernovas, existem discontinuidades em densidade,
que tornam o problema mais complexo. Neste caso precisamos usar
outras técnicas, como as descritas por Yakov Borisovich
Zel'dovich (1914-1987) e Yuri P. Raizer no
seu livro Physics of Shock Waves and High Temperature
Hydrodynamic Phenomena, 1966, eds. W.D. Hayes e R.F. Probstein
(New York: Academic Press).
Naturalmente a escolha do passo de tempo, 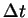 depende de
quão rapidamente o sistema está mudando no tempo em questão.
Se o sistema está mudando rapidamente,
depende de
quão rapidamente o sistema está mudando no tempo em questão.
Se o sistema está mudando rapidamente, 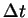 precisa
ser pequeno.
O passo em tempo deveria ser menor do que o tempo em que uma onda sonora
leva para atravessar uma camada. Examinando-se todas as camadas,
escolhe-se o limite superior do passo. Esta condição chama-se
condição de Courant [Richard Courant (1888-1972),
Kurt Friedrichs & Hans Lewy, (1928), Über die partiellen Differenzengleichungen der mathematischen Physik, Mathematische Annalen, 100, 32].
Mas na sequência principal, a escala de tempo importante não é a das ondas sonoras, da ordem de alguns segundos,
mas sim a escala términa,
da ordem de dezenas de milhões de anos.
Uma maneira de aumentar o passo temporal é escrever as diferenças temporais, por
exemplo dP/dt≈(Pn+1-Pn)/\Delta t, de modo que
as derivadas dependem também da variável em um tempo tn+1
e são calculados simultaneamente no processo iterativo, no
chamado esquema implícito.
O maior passo possível também depende
da estabilidade numérica.
Desta maneira calculam-se as acelerações e as velocidades,
corrige-se o raio e calculam-se as novas densidades. Então
calculam-se as novas temperaturas. Se o modelo for hidrostático,
as acelerações serão nulas. O raio para um tempo qualquer
precisa ser calculado simultaneamente com as outras variáveis.
Como reações nucleares estão quase sempre presentes, precisamos
incluir a mudanças nas abundâncias. Como as mudanças
no peso molecular médio devido à ionização são muito
rápidas, elas são incorporadas à equação de estado.
Exceto em situações especiais, as abundâncias mudam
vagarosamente e podem ser calculadas como simples diferenças.
precisa
ser pequeno.
O passo em tempo deveria ser menor do que o tempo em que uma onda sonora
leva para atravessar uma camada. Examinando-se todas as camadas,
escolhe-se o limite superior do passo. Esta condição chama-se
condição de Courant [Richard Courant (1888-1972),
Kurt Friedrichs & Hans Lewy, (1928), Über die partiellen Differenzengleichungen der mathematischen Physik, Mathematische Annalen, 100, 32].
Mas na sequência principal, a escala de tempo importante não é a das ondas sonoras, da ordem de alguns segundos,
mas sim a escala términa,
da ordem de dezenas de milhões de anos.
Uma maneira de aumentar o passo temporal é escrever as diferenças temporais, por
exemplo dP/dt≈(Pn+1-Pn)/\Delta t, de modo que
as derivadas dependem também da variável em um tempo tn+1
e são calculados simultaneamente no processo iterativo, no
chamado esquema implícito.
O maior passo possível também depende
da estabilidade numérica.
Desta maneira calculam-se as acelerações e as velocidades,
corrige-se o raio e calculam-se as novas densidades. Então
calculam-se as novas temperaturas. Se o modelo for hidrostático,
as acelerações serão nulas. O raio para um tempo qualquer
precisa ser calculado simultaneamente com as outras variáveis.
Como reações nucleares estão quase sempre presentes, precisamos
incluir a mudanças nas abundâncias. Como as mudanças
no peso molecular médio devido à ionização são muito
rápidas, elas são incorporadas à equação de estado.
Exceto em situações especiais, as abundâncias mudam
vagarosamente e podem ser calculadas como simples diferenças.
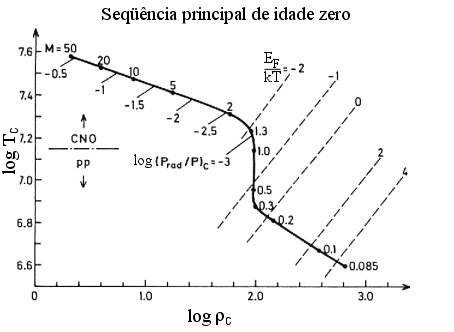 Densidade central e temperatura central para estrelas
na seqüência principal de idade zero,
com X=0,685 e Y=0,295. Para as estrelas de baixa massa,
EF/kT > 1, indicando que os elétrons estão
degenerados. As massas, M, estão em massas solares.
A contribuição do ciclo CNO para a geração de energia
passa de 3% para
1
Densidade central e temperatura central para estrelas
na seqüência principal de idade zero,
com X=0,685 e Y=0,295. Para as estrelas de baixa massa,
EF/kT > 1, indicando que os elétrons estão
degenerados. As massas, M, estão em massas solares.
A contribuição do ciclo CNO para a geração de energia
passa de 3% para
1  a 90% para
3
a 90% para
3 
Como
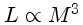 ,
,
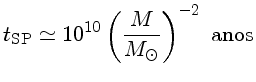 |
(65) |
para as estrelas acima de 3  . Esta relação
indica que para uma estrela de
. Esta relação
indica que para uma estrela de
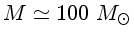 ,
a sequência principal dura apenas 1 milhão de anos.
,
a sequência principal dura apenas 1 milhão de anos.
Em 1942 o brasileiro
Mário Schenberg (1916-1990) e o
indiano
Subrahmanyan Chandrasekhar (1910-1995),
demonstraram que quando o núcleo isotérmico de hélio
corresponde a 10% da massa inicial de hidrogênio da estrela, não
é mais possível manter o equilíbrio hidrostático no
núcleo se a pressão é dada por um gás ideal. Este é
o chamado limite de Schenberg-Chandrasekhar, e os modelos
evolucionários comprovam que o núcleo se contrai rapidamente,
esquentando e aumentando a produção de
energia. A região em volta do núcleo se expande
rapidamente e a estrela sai da sequência principal.
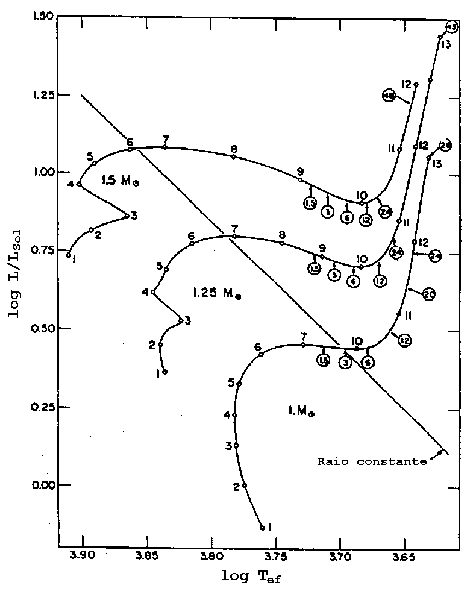
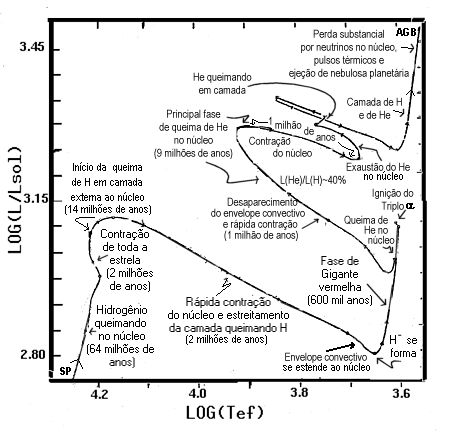 Diagrama HR teórico mostrando as diversas
evolução de uma estrela de 5 massas solares,
a partir da sequência principal (SP), no extremo esquerdo inferior, e
quanto tempo a estrela leva em cada fase, segundo os cálculos de
Icko Iben Jr.
Diagrama HR teórico mostrando as diversas
evolução de uma estrela de 5 massas solares,
a partir da sequência principal (SP), no extremo esquerdo inferior, e
quanto tempo a estrela leva em cada fase, segundo os cálculos de
Icko Iben Jr.
 Foto de Icko Iben Jr. (1931-), que estudou com
Martin Schwarzschild (1912-1997), o precursor dos
cálculos de modelos de evolução estelar. Icko Iben
continuou este trabalho e é considerado o maior especialista
no assunto.
Foto de Icko Iben Jr. (1931-), que estudou com
Martin Schwarzschild (1912-1997), o precursor dos
cálculos de modelos de evolução estelar. Icko Iben
continuou este trabalho e é considerado o maior especialista
no assunto.
Icko Iben Jr. e
Gregory Laughlin, no seu artigo publicado em 1989 no
Astrophysical Journal, 341, 312, fitaram os resultados
do tempo de vida desde a sequência principal até a fase
de nebulosa planetária dos modelos com
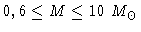 e encontraram
e encontraram
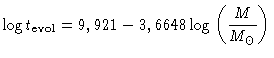 |
(66) |
para idade em anos.
Por exemplo, para um modelo de 0,7  ,
obtemos um tempo de evolução de 35 Ganos, algumas vezes maior do
que a idade do Universo.
Estes modelos não levavam em conta o difusão dos elementos na sequência
principal, que reduz o tempo de vida porque parte do hidrogênio é
transportado para cima, por ser mais leve, reduzindo o combustível no
núcleo
Paula Jofré e Achim Weiss,
Astronomy & Astrophysics de 2011, 533, 15].
,
obtemos um tempo de evolução de 35 Ganos, algumas vezes maior do
que a idade do Universo.
Estes modelos não levavam em conta o difusão dos elementos na sequência
principal, que reduz o tempo de vida porque parte do hidrogênio é
transportado para cima, por ser mais leve, reduzindo o combustível no
núcleo
Paula Jofré e Achim Weiss,
Astronomy & Astrophysics de 2011, 533, 15].
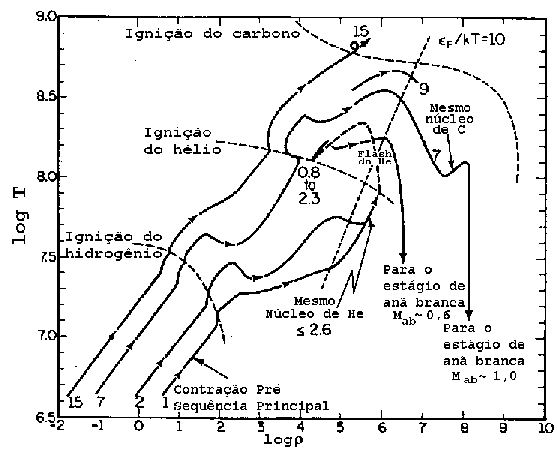
Densidade e temperaturas centrais para modelos evolucionários
de Icko Iben Jr. (1974, Annual Review of Astronomy and Astrophysics, 12, 271)
para estrelas entre 0,8 e 15 massas solares.
A linha pontilhada
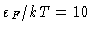
indica
quando a pressão de degenerescência dos elétrons domina. A direita
da linha o gás é degenerado e a esquerda, não degenerado.
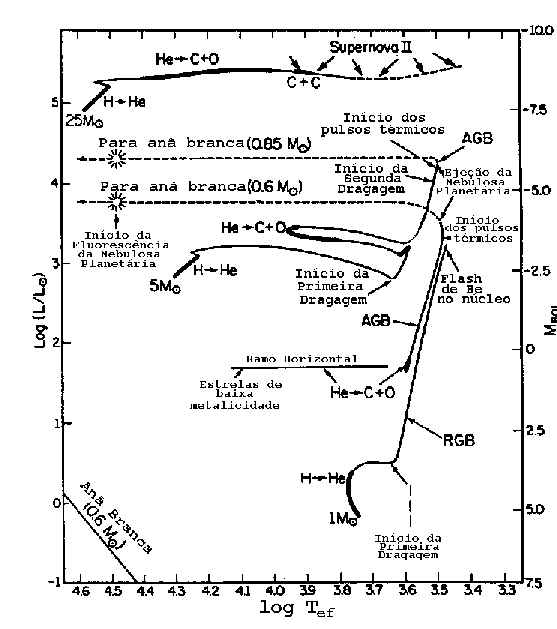
Evolução a partir da seqüência principal para
modelos de 1, 5 e 25 massas solares. A queima de combustível
no núcleo ocorre nas regiões mais escuras das curvas.
Durante a fase interpulso, o He produzido pela camada termonuclear dominante,
de queima de H, é acumulado na camada de He, até que um flash
de He ocorra, que induz a uma zona de convecção entre as camadas.
A terceira dragagem ocorre durante a fase de pulsos térmicos,
e é onde se formam as estrelas carbonadas
e estrelas ricas em ZrO.
A opacidade das moléculas na
atmosfera, que está mudando com a dragagem,
bem como o aumento da perda de massa com a metalicidade,
precisa
ser incluída nos modelos.
Nos modelos de Leo Girardi e Paola Marigo,
a fase das estrelas carbonadas dura entre 2 e 3 milhões de anos.
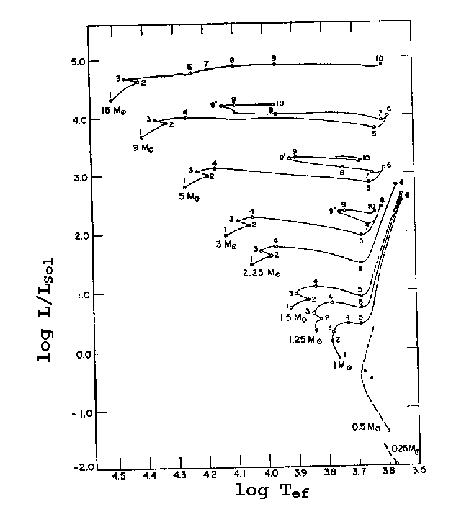
Iben e Renzini fitaram seus modelos teóricos a uma relação
entre a idade dos cúmulos e o turnoff point - TOP, que
é a luminosidade para a qual as estrelas começam
a sair da sequência principal:
onde 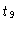 é a idade do cúmulo, em unidades de
é a idade do cúmulo, em unidades de 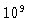 anos. Estes modelos são antigos,
com tabelas de opacidades e taxas de reação nuclear antigas,
não levam em conta a difusão, e resultam em
idades irreais, de até 20 Ganos.
anos. Estes modelos são antigos,
com tabelas de opacidades e taxas de reação nuclear antigas,
não levam em conta a difusão, e resultam em
idades irreais, de até 20 Ganos.
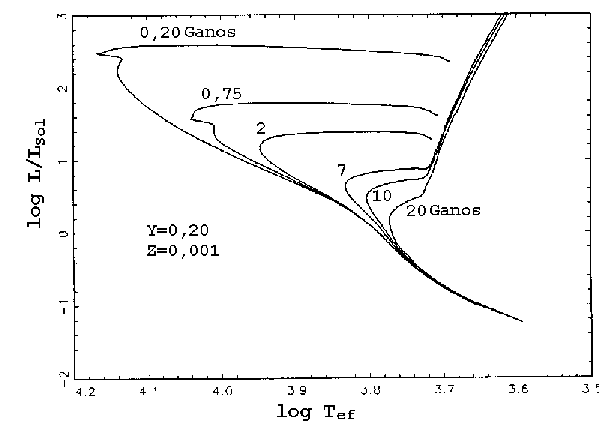
Isócronas teóricas.
Léo Girardi e colaboradores, no artigo de 2010 no Astrophysical Journal, 724, 1030, como os
modelos de Padova, calcularam uma redução no tempo de vida no TP-AGB (thermally pulsating assymptotic giant
branch - fase de pulsos térmicos no ramo assintótico das supergigantes) de 5 para 1,4 milhões de anos,
para estrelas de Z=0,001 e M=0,7 a 0,9 MSol, devido à inclusão nos cálculos das opacidades
moleculares e da perda de massa por
poeira (dust-driven winds). Estas estrelas de baixa metalicidade não passam pela dragagem
no TP-AGB e são predominantemente ricas em O. Além da redução em idade, há também uma
redução na massa final resultante, que passa de 0,55 a 0.65MSol para massas iniciais
de 0,7 a 0,9 MSol, para 0,51 a 0,55 MSol.
Paula Jofré e Achim Weiss
mostram no seu artigo no Astronomy & Astrophysics de 2011, 533, 15,
que se não levam em conta a difusão nas estrelas
do halo na nossa Galáxia, a idade obtida é de 14 a 16 Ganos,
incoerente com a idade do Universo. Quando levam em conta
a difusão,
como o hidrogênio difunde para cima, saindo do núcleo,
existe menos combustível nuclear e
a saída da sequência principal é mais rápida.
Neste caso a idade é de 10 a 12 Ganos, comprovando então que
é necessário levar em conta a difusão na evolução estelar,
especialmente para as estrelas de baixa metalicidade, que
têm envelope convectivo razo e há difusão por um longo tempo.
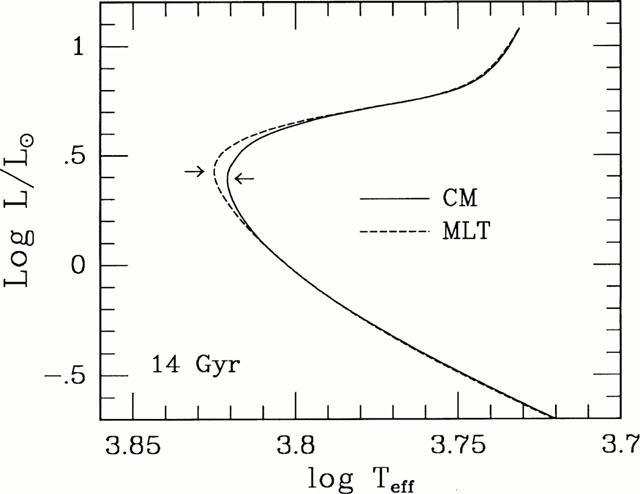
Comparação do modelo de Italo Mazitelli, Franca D'Antona e Vittoria Caloi, 1995, Astronomy & Astrophysics, 302, 382,
com Z=0,0001 e idade de 14 Ganos,
com dois tratamentos diferentes
de convecção, a teoria do comprimento de mistura, MLT, e
a teoria de Vittorio M. Canuto e Italo Mazzitelli de multiplas escalas..
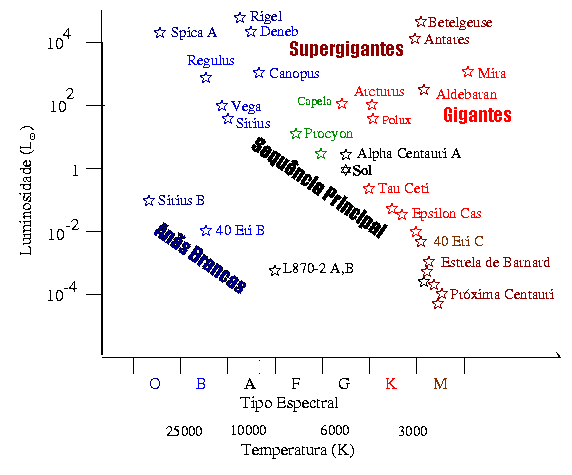
As estrelas brilhantes como Rigel, Deneb, Capela e Polux
estão em uma linha aproximadamente paralela à sequência
e estão queimando hélio em seu núcleo, na chamada
sequência principal do hélio
[Bodan Paczynski (1940-2007), 1971, Evolution of Single Stars. IV. Helium Stars, Acta Astronomica, Vol. 21, p.1].
As estrelas Betelgeuse, Mira, Antares e Aldebaran têm aproximadamente
a mesma temperatura efetiva são chamadas de supergigantes
vermelhas. As menos brilhantes estão queimando
hidrogênio em uma camada sobre o núcleo compacto,
comparável em tamanho as anãs brancas menos massivas
conhecidas. As estrelas como a Mira alternam entre queimando
hidrogênio e queimando hélio em camadas sobre um núcleo
de carbono e oxigênio
similar às anãs brancas. Estas estrelas pertencem ao
Ramo Gigante Assintótico (AGB), são pulsantes térmicas,
e passam por estágios de queima termonuclear descontrolada
intermitente. Elas são responsáveis pela formação
da maioria do carbono e dos isótopos ricos em nêutrons
formados pelo processo lento de captura de nêutrons.
Aproximadamente 80% da fase da vida de uma estrela em que ocorrem
reações nucleares é passada na sequência principal. Se
a estrela tiver massa acima de 1,25  a conversão de
hidrogênio em hélio se dá pelo ciclo CNO, em um núcleo
convectivo, se a estrela possui carbono.
Depois de consumir o hidrogênio central, a estrela
se desloca rapidamente para o ramo das gigantes, queimando hidrogênio
em uma camada fina sobre o núcleo em rápida contração e
aquecimento, composto essencialmente de hélio puro.
Como a camada é fina, a temperatura em que ocorre a queima é
significativamente maior do que quando houve queima no núcleo,
já que a mesma luminosidade tem que ser gerada em uma camada com
menor massa.
Com a contração do núcleo, há expansão
das camadas externas.
Ao se
aproximar do ramo das gigantes, a base da região
convectiva superficial se extende até as camadas em que
o carbono foi convertido em nitrogênio; a abundância
superficial destes dois elementos começa a mudar em
quantidades detectáveis. Este processo de mistura
convectiva de elementos processados termonuclearmente
no núcleo convectivo é chamado de primeira dragagem
( first dredge-up).
a conversão de
hidrogênio em hélio se dá pelo ciclo CNO, em um núcleo
convectivo, se a estrela possui carbono.
Depois de consumir o hidrogênio central, a estrela
se desloca rapidamente para o ramo das gigantes, queimando hidrogênio
em uma camada fina sobre o núcleo em rápida contração e
aquecimento, composto essencialmente de hélio puro.
Como a camada é fina, a temperatura em que ocorre a queima é
significativamente maior do que quando houve queima no núcleo,
já que a mesma luminosidade tem que ser gerada em uma camada com
menor massa.
Com a contração do núcleo, há expansão
das camadas externas.
Ao se
aproximar do ramo das gigantes, a base da região
convectiva superficial se extende até as camadas em que
o carbono foi convertido em nitrogênio; a abundância
superficial destes dois elementos começa a mudar em
quantidades detectáveis. Este processo de mistura
convectiva de elementos processados termonuclearmente
no núcleo convectivo é chamado de primeira dragagem
( first dredge-up).
Para uma estrela
de massa intermediária, isto é, acima de 2,3  (ou acima de 1,8
(ou acima de 1,8  se overshooting for significativo),
a temperatura central atingirá
se overshooting for significativo),
a temperatura central atingirá
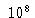 K e a densidade central
K e a densidade central
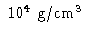 em um núcleo não degenerado, e o
hélio começará a ser transformado em carbono no centro,
revertendo a ascensão da estrela no ramo das gigantes
no diagrama H-R.
A liberação de energia expande o núcleo
e as camadas externas se contraem, aumentando
a temperatura efetiva de cerca de 4000 K para 8000 K.
A estrela então passará uma longa fase
de queima de hélio em um núcleo convectivo e em crescimento.
A queima de hidrogênio em uma camada fina continua a
prover a maior parte da luminosidade da estrela (80%) e, portanto,
a massa da região central exaurida de hidrogênio continua
a aumentar.
Alfred Gautschy (2012)
faz um resumo da ignição de hélio fora do centro em um gás degenerado
para estrelas até 2 massas solares. A ignição fora de centro, causada
pela forte emissão de neutrinos no centro, foi primeiro estudada por
Hans-Christoph Thomas em 1967, no
Zeitschrift für Astrophysik, 67, 420.
em um núcleo não degenerado, e o
hélio começará a ser transformado em carbono no centro,
revertendo a ascensão da estrela no ramo das gigantes
no diagrama H-R.
A liberação de energia expande o núcleo
e as camadas externas se contraem, aumentando
a temperatura efetiva de cerca de 4000 K para 8000 K.
A estrela então passará uma longa fase
de queima de hélio em um núcleo convectivo e em crescimento.
A queima de hidrogênio em uma camada fina continua a
prover a maior parte da luminosidade da estrela (80%) e, portanto,
a massa da região central exaurida de hidrogênio continua
a aumentar.
Alfred Gautschy (2012)
faz um resumo da ignição de hélio fora do centro em um gás degenerado
para estrelas até 2 massas solares. A ignição fora de centro, causada
pela forte emissão de neutrinos no centro, foi primeiro estudada por
Hans-Christoph Thomas em 1967, no
Zeitschrift für Astrophysik, 67, 420.
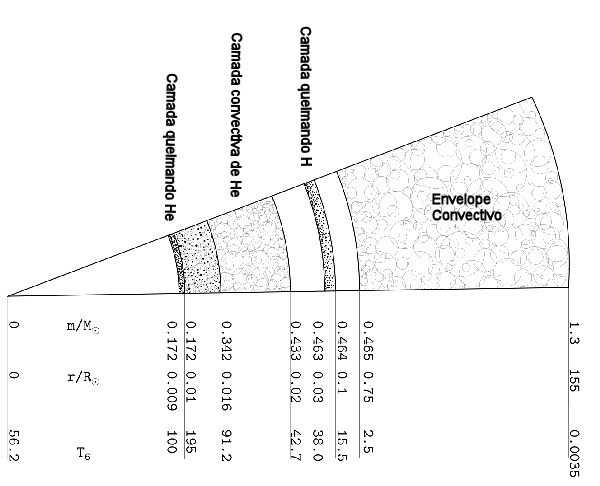 Modelo estrutural de uma estrela de 1,3 massas solares
no início da queima de He, calculado por Alfred Gautschy.
Modelo estrutural de uma estrela de 1,3 massas solares
no início da queima de He, calculado por Alfred Gautschy.
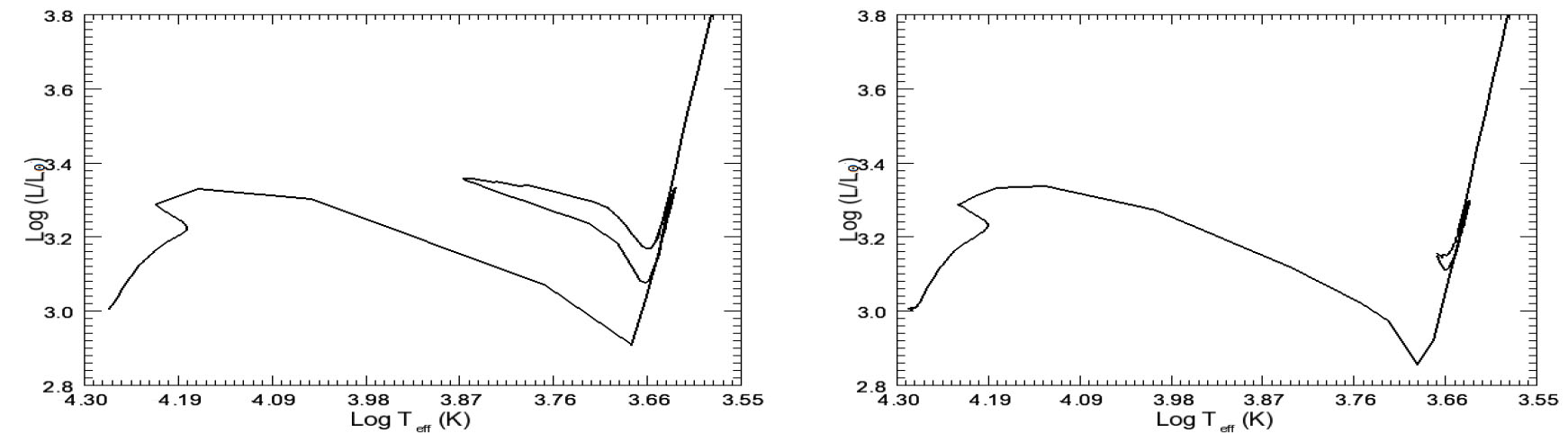
Ghina M. Halabi, no seu
artigo de 2014 no 2014arXiv1410.1651H,
calcula o efeito
da nova taxa reduzida (Cyburt et al. 2010, Astrophysical Journal Supplement Series, 189, 240) (direita) de
14N(p,γ)
15O para
um modelo de 6 M
Sol com metalicidade solar, que reduz o loop da queima de hélio,
em relação ao modelo com a taxa do NACRE (esquerda).
Quando a abundância do hélio central decresce significativamente,
o hélio continua a queimar em uma camada externa que se desloca
para massas maiores. O núcleo exaurido de hélio se contrai e
esquenta enquanto que a envelope rico em hidrogênio se expande e
esfria tanto que o hidrogênio para de queimar. No diagrama
H-R o modelo evolui novamente para o ramo das (super-)gigantes e a base
do envelope convectivo se estende até a interface
hidrogênio-hélio, entrando em camadas em que o hidrogênio
foi completamente convertido em hélio e a maior parte
do carbono original convertido em nitrogênio. Hélio
e nitrogênio são trazidos para a superfície
na segunda dragagem.
A matéria na base do envelope convectivo é aquecida
até reiniciar a queima do hidrogênio, o que força
a base do envelope convectivo a recuar para uma região
acima da camada onde ocorre a queima de hidrogênio.
Para uma estrela de 5  ,
logo após o início da segunda dragagem a matéria
no núcleo exaurido de hélio atinge
,
logo após o início da segunda dragagem a matéria
no núcleo exaurido de hélio atinge
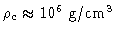 e os elétrons se tornam degenerados. Nestas condições,
a condução de calor pelos elétrons ajuda a manter a
matéria nuclear dentro de um fator de 2 da temperatura média
do núcleo,
e os elétrons se tornam degenerados. Nestas condições,
a condução de calor pelos elétrons ajuda a manter a
matéria nuclear dentro de um fator de 2 da temperatura média
do núcleo,
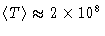 K,
e a perda de energia pelos processos de plasma
e foto-neutrinos se tornam importantes. Grande parte da liberação
de energia gravitacional potencial pelas camadas superiores
é perdida pela emissão de neutrinos, mantendo a temperatura
do núcleo próxima da temperatura da camada onde ocorre
a queima de hélio. O núcleo da estrela tem as dimensões
de uma anã branca, e é de fato uma anã branca quente.
K,
e a perda de energia pelos processos de plasma
e foto-neutrinos se tornam importantes. Grande parte da liberação
de energia gravitacional potencial pelas camadas superiores
é perdida pela emissão de neutrinos, mantendo a temperatura
do núcleo próxima da temperatura da camada onde ocorre
a queima de hélio. O núcleo da estrela tem as dimensões
de uma anã branca, e é de fato uma anã branca quente.
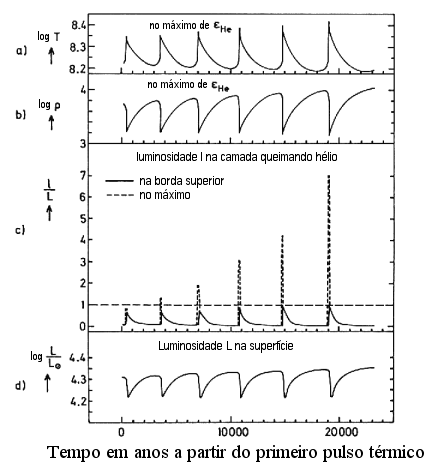 Pulsos térmicos para uma estrela de
5
Pulsos térmicos para uma estrela de
5  depois da queima do hélio nuclear, segundo o cálculo de Alfred Weigert
(1966, Zeitschrift für Astrophysik, 64, 395).
depois da queima do hélio nuclear, segundo o cálculo de Alfred Weigert
(1966, Zeitschrift für Astrophysik, 64, 395).
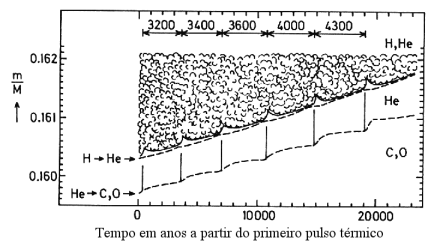 Evolução da região próxima das duas camadas
com reações nucleares (linhas tracejadas). A região com bolhas
representa a zona de convecção externa. A zona de convecção na
região entre as camadas, no máximo de cada pulso, é tão rápida
que aparece no gráfico somente como um traço vertical. O tempo
entre cada pulso consecutivo, em anos, é indicado no topo da
figura. Alfred Weigert
(1966, Zeitschrift für Astrophysik, 64, 395).
Evolução da região próxima das duas camadas
com reações nucleares (linhas tracejadas). A região com bolhas
representa a zona de convecção externa. A zona de convecção na
região entre as camadas, no máximo de cada pulso, é tão rápida
que aparece no gráfico somente como um traço vertical. O tempo
entre cada pulso consecutivo, em anos, é indicado no topo da
figura. Alfred Weigert
(1966, Zeitschrift für Astrophysik, 64, 395).
A queima de hidrogênio e hélio ocorre alternadamente em camadas,
ocorre extensa nucleosíntese por captura de nêutrons,
sintetizando centenas de isótopos ricos em nêutrons, e dependendo da metalicidade, estes
isótopos, junto com o carbono, são trazidos para
a superfície em uma série de episódios
de terceira dragagem.
Nos modelos teóricos com pouca perda de massa, a massa do núcleo
central de carbono e oxigênio cresce até atingir 1,4  ,
o limite de Chandrasekhar. Neste ponto o carbono começa a queimar,
pois há forte escudamento eletrônico,
e depois de um curto episódio durante o qual a
perda de energia pelo processo Urca balança a energia
gerada pela queima do carbono, a taxa de queima
de carbono cresce exponencialmente, criando uma frente que queima
que se desloca na direção da superfície,
convertendo matéria em elementos do grupo do ferro,
mas com velocidades acima da velocidade de escape.
Desta forma, o núcleo é completamente desfeito
como uma supernova.
Nos modelos com maior perda de massa, o início da queima do
C ocorre antes do núcleo atingir a massa de Chandrasekhar.
A massa do envelope rico em hidrogênio do modelo de supernova é grande
o suficiente para que linhas de hidrogênio sejam proeminentes.
Estas são as SN II.
,
o limite de Chandrasekhar. Neste ponto o carbono começa a queimar,
pois há forte escudamento eletrônico,
e depois de um curto episódio durante o qual a
perda de energia pelo processo Urca balança a energia
gerada pela queima do carbono, a taxa de queima
de carbono cresce exponencialmente, criando uma frente que queima
que se desloca na direção da superfície,
convertendo matéria em elementos do grupo do ferro,
mas com velocidades acima da velocidade de escape.
Desta forma, o núcleo é completamente desfeito
como uma supernova.
Nos modelos com maior perda de massa, o início da queima do
C ocorre antes do núcleo atingir a massa de Chandrasekhar.
A massa do envelope rico em hidrogênio do modelo de supernova é grande
o suficiente para que linhas de hidrogênio sejam proeminentes.
Estas são as SN II.
Como por definição uma supernova do tipo Ia não tem linhas
de hidrogênio, supernova SN Ia não é oriunda
da evolução de uma estrela de massa intermediária
sem perda de massa significativa. Na verdade os modelos
indicam que as supernovas tipo Ia são formadas por acresção
de massa em estrelas anãs brancas, já que neste caso a
temperatura é suficiente para queimar todo o hidrogênio.
As supernovas formadas pelas estrelas de massa intermediária são
supernovas do tipo II. Como a taxa de nascimento de estrelas na nossa
galáxia é de aproximadamente uma estrela por ano, o número
de estrelas com massa inicial superior a 1,4  ,
de acordo com a função de massa proposta em 1955 pelo
astrônomo americano
Edwin Ernest Salpeter (1925-2008)
que dá a taxa de formação de estrelas por
,
de acordo com a função de massa proposta em 1955 pelo
astrônomo americano
Edwin Ernest Salpeter (1925-2008)
que dá a taxa de formação de estrelas por
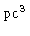 por ano
por ano
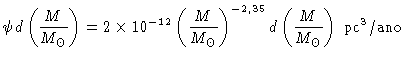 |
(67) |
corresponde a 20 vezes a taxa de formação de supernovas
na nossa galáxia, concluímos que a maior parte
das estrelas de massa intermediária termina de alguma
forma sua vida antes da queima explosiva do carbono.
Estrelas reais perdem seus envelopes ricos em hidrogênio
antes que o núcleo comece a queimar o carbono.
Se supormos que as supernovas só ocorrem
para massas iniciais acima de
10  ,
a taxa se torna uma a cada 39 anos, próxima
da estimativa atual de uma a cada 50 anos na Galáxia.
,
a taxa se torna uma a cada 39 anos, próxima
da estimativa atual de uma a cada 50 anos na Galáxia.
A estimativa da taxa de formação de nebulosas planetárias
na nossa galáxia é consistente com a estimativa de formação
de estrelas de massas baixa e intermediária,
isto é, até 10  .
Philipp Podsiadlowski et al. 2004, Astrophysical Journal, 612, 1044 estimam
11±1
.
Philipp Podsiadlowski et al. 2004, Astrophysical Journal, 612, 1044 estimam
11±1  como o limite inferior para a massa das estrelas
que geram estrelas de nêutrons.
Stephen J. Smartt, no seu artigo
Progenitors of Core-Collapse Supernovae, de
2009 no Annual Review of Astronomy & Astrophysics, 47, 63,
e com
J. J. Eldridge, R. M. Crockett, & J. R.Maund, no
The death of massive stars - I. Observational constraints on the progenitors of Type II-P supernovae,
publicado em 2009 no Monthly Notices of the Royal Astronomical Sociery, 395, 1409,
concluem que estrelas com massa superior a 8,5±1,5 MSol
tornam-se supernovas tipo II.
como o limite inferior para a massa das estrelas
que geram estrelas de nêutrons.
Stephen J. Smartt, no seu artigo
Progenitors of Core-Collapse Supernovae, de
2009 no Annual Review of Astronomy & Astrophysics, 47, 63,
e com
J. J. Eldridge, R. M. Crockett, & J. R.Maund, no
The death of massive stars - I. Observational constraints on the progenitors of Type II-P supernovae,
publicado em 2009 no Monthly Notices of the Royal Astronomical Sociery, 395, 1409,
concluem que estrelas com massa superior a 8,5±1,5 MSol
tornam-se supernovas tipo II.
 Nebulosa Planetária da Helix, fotografada pelo Telescópio
Espacial Hubble. Existem aproximadamente 10 000 nebulosas planetárias
em nossa galáxia. A nebulosidade permanece visível por aproximadamente
10 000 anos após sua ejeção pela estrela, no ramo gigante assintótico.
O termo nebulosa planetária foi dado porque algumas se parecem
com o planeta Urano, quando olhadas através de um telescópio pequeno.
Nebulosa Planetária da Helix, fotografada pelo Telescópio
Espacial Hubble. Existem aproximadamente 10 000 nebulosas planetárias
em nossa galáxia. A nebulosidade permanece visível por aproximadamente
10 000 anos após sua ejeção pela estrela, no ramo gigante assintótico.
O termo nebulosa planetária foi dado porque algumas se parecem
com o planeta Urano, quando olhadas através de um telescópio pequeno.
Após a ejeção da maior parte do envelope de hidrogênio na fase de nebulosa
planetária,
o núcleo remanescente de um modelo de estrela com massa inicial
de até aproximadamente 10  evolui rapidamente para o azul no diagrama H-R, em uma
trajetória essencialmente horizontal. A luminosidade do
modelo é ainda devido à queima de hidrogênio em uma camada
fina, mas, quando a temperatura efetiva do modelo atinge
evolui rapidamente para o azul no diagrama H-R, em uma
trajetória essencialmente horizontal. A luminosidade do
modelo é ainda devido à queima de hidrogênio em uma camada
fina, mas, quando a temperatura efetiva do modelo atinge
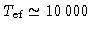 K, a quantidade total de hidrogênio
acima da camada é tão pequena que a queima só continua
por aproximadamente 300 anos. Quando a temperatura
efetiva atinge 30000 K, o material ejetado pode ser
fotoionizado pela radiação do remanescente compacto
e o sistema terá as características de uma nebulosa
planetária com uma estrela central quente.
K, a quantidade total de hidrogênio
acima da camada é tão pequena que a queima só continua
por aproximadamente 300 anos. Quando a temperatura
efetiva atinge 30000 K, o material ejetado pode ser
fotoionizado pela radiação do remanescente compacto
e o sistema terá as características de uma nebulosa
planetária com uma estrela central quente.
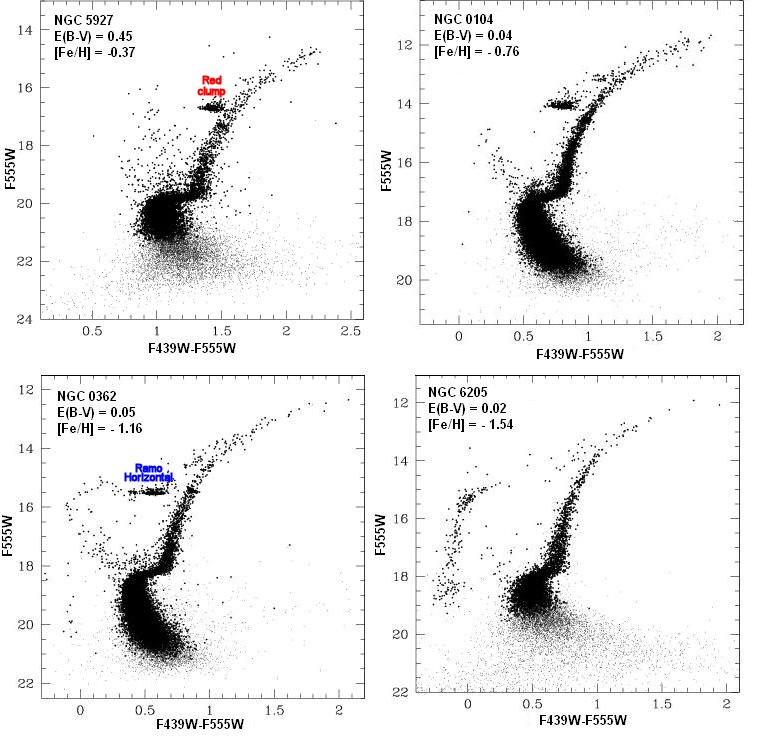 Diagramas cor magnitude de aglomerados
de metalicidades diferentes, mostrando Red Clump ou Ramo Horizontal,
com dados do Telescópio Espacial Hubble publicados por
Gianpaolo Piotto et al. (2002), Astronomy & Astrophysics, 391, 945
Diagramas cor magnitude de aglomerados
de metalicidades diferentes, mostrando Red Clump ou Ramo Horizontal,
com dados do Telescópio Espacial Hubble publicados por
Gianpaolo Piotto et al. (2002), Astronomy & Astrophysics, 391, 945
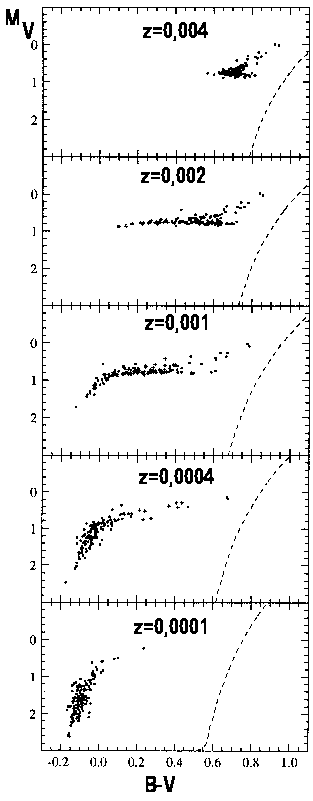 O ramo horizontal é onde as estrelas queimam He no núcleo. As estrelas
com massa até cerca de 3
O ramo horizontal é onde as estrelas queimam He no núcleo. As estrelas
com massa até cerca de 3 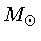 chegam ao ramo horizontal
com um núcleo com aproximadamente 0,6
chegam ao ramo horizontal
com um núcleo com aproximadamente 0,6 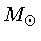 .
Nos modelos de
Young-Wook Lee, Pirre Demarque e Robert Zinn, mostrados na figura ao lado e publicados no artigo The Horizontal-Branch Stars in Globular Clusters. II. The Second Parameter Phenomenon em 1994, no Astrophysical Journal,
423, 248, eles mostram que a diferença na idade e na metalicidade dos
aglomerados explica a variedade de ramos horizontais observados.
.
Nos modelos de
Young-Wook Lee, Pirre Demarque e Robert Zinn, mostrados na figura ao lado e publicados no artigo The Horizontal-Branch Stars in Globular Clusters. II. The Second Parameter Phenomenon em 1994, no Astrophysical Journal,
423, 248, eles mostram que a diferença na idade e na metalicidade dos
aglomerados explica a variedade de ramos horizontais observados.
No Ramo Horizontal, as
estrelas apresentam
variações de luz, causadas pelas zonas de ionização parcial
do hidrogênio e do hélio, e são chamadas de
variáveis RR Lyrae.
Os modelos hidrodinâmicos das variações mostram que as RR Lyrae
têm massa entre 0,6 e 0,7 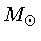 , embora os precursores
sejam mais massivos, indicando que já perderam uma quantidade
significativa de massa durante sua evolução, mas principalmente
no ramo das gigantes.
, embora os precursores
sejam mais massivos, indicando que já perderam uma quantidade
significativa de massa durante sua evolução, mas principalmente
no ramo das gigantes.
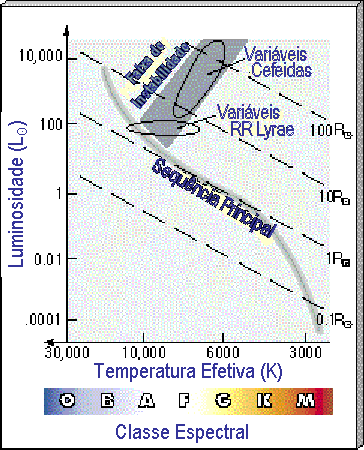
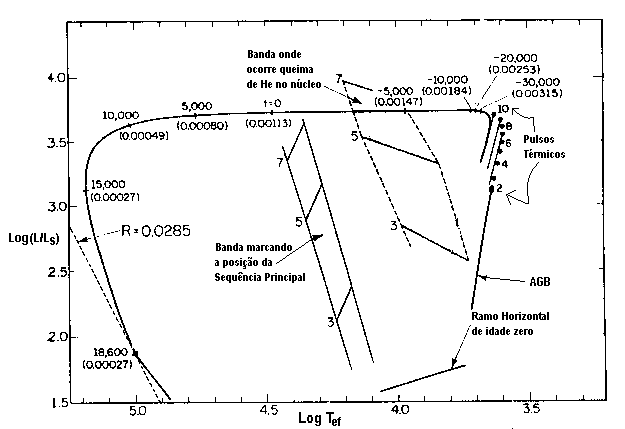 Diagrama HR teórico mostrando o caminho evolucionário de
uma estrela de 0,6
Diagrama HR teórico mostrando o caminho evolucionário de
uma estrela de 0,6 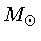 , a partir do Ramo Horizontal,
calculado pelo americano Icko Iben Jr.
e pelo italiano Alvio Renzini (1983, Annual Review of Astronomy and
Astrophysics, 21, 271), para X=0,749 e Y=0,25.
, a partir do Ramo Horizontal,
calculado pelo americano Icko Iben Jr.
e pelo italiano Alvio Renzini (1983, Annual Review of Astronomy and
Astrophysics, 21, 271), para X=0,749 e Y=0,25.
Estrelas mais massivas,
com massas
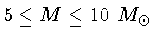 , tornam-se
pulsantes quando ainda estão queimando He no núcleo, mas com
períodos mais longos, da ordem de dias, e são chamadas de
Cefeidas.
Elas são usadas como indicadores de distância para
as galáxias, pois seu período de pulsação é
proporcional à sua luminosidade,
como descoberto em 1912 por
Henrietta Swan Leavitt
(1868-1921).
, tornam-se
pulsantes quando ainda estão queimando He no núcleo, mas com
períodos mais longos, da ordem de dias, e são chamadas de
Cefeidas.
Elas são usadas como indicadores de distância para
as galáxias, pois seu período de pulsação é
proporcional à sua luminosidade,
como descoberto em 1912 por
Henrietta Swan Leavitt
(1868-1921).
As Cefeidas clássicas têm
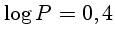 a 1,8, em dias, a 1,8, em dias,
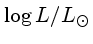 =2,81 a 4,58, =2,81 a 4,58,
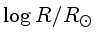 =1,41 a 2,44, =1,41 a 2,44,
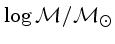 =0,54 a 1,04, e =0,54 a 1,04, e
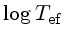 =3,76 a 3,69. =3,76 a 3,69.
|
As Cefeidas de População II têm
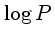 =0,1 a 1,3, em dias, =0,1 a 1,3, em dias,
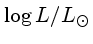 =1,95 a 2,87, =1,95 a 2,87,
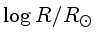 =0,86 a 1,52, =0,86 a 1,52,
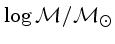 =-0,22, e =-0,22, e
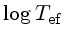 =3,82 a 3,72. =3,82 a 3,72.
|
Se não houvesse overshooting, a massa mínima para
que uma estrela de população I queimasse o hélio em
um núcleo não degenerado seria da ordem de 2,3  .
Com overshooting este limite inferior pode ser de até
1,5
.
Com overshooting este limite inferior pode ser de até
1,5  , mas uma comparação com as observações
sugere um limite entre 1,6
, mas uma comparação com as observações
sugere um limite entre 1,6  e 2,1
e 2,1  .
.
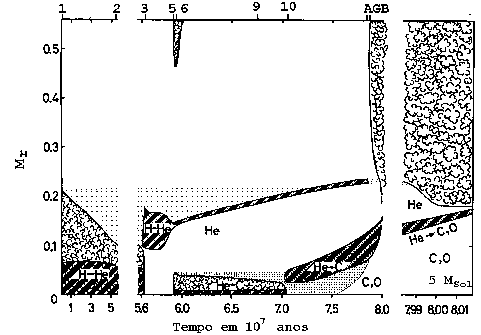 Evolução da estrutura interna de uma estrela de 5
Evolução da estrutura interna de uma estrela de 5 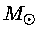 após a
seqüência principal. Os números na parte superior da figura
correspondem às fases equivalentes da figura
evolucionária. As regiões
escuras indicam queima nuclear e as com bolhas indicam convecção
(Rudolf Kippenhahn, Hans-Christoph Thomas & Alfred Weigert, 1965, Zeitschrift für Astrophysik, 61, 241).
após a
seqüência principal. Os números na parte superior da figura
correspondem às fases equivalentes da figura
evolucionária. As regiões
escuras indicam queima nuclear e as com bolhas indicam convecção
(Rudolf Kippenhahn, Hans-Christoph Thomas & Alfred Weigert, 1965, Zeitschrift für Astrophysik, 61, 241).
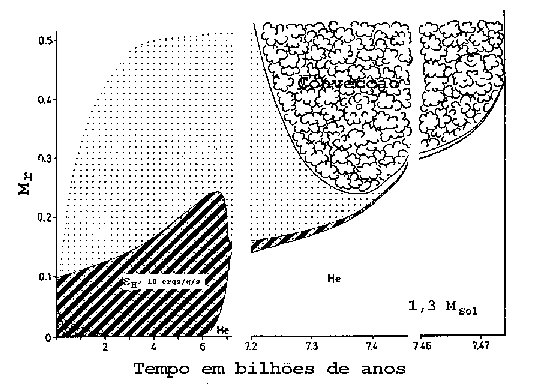 Evolução da estrutura interna de uma estrela de 1,3
Evolução da estrutura interna de uma estrela de 1,3 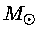 após a seqüência principal.
A região pontilhada é onde a abundância de hidrogênio muda (Hans-Christoph Thomas, 1967, Zeitschrift für Astrophysik, 67, 420).
após a seqüência principal.
A região pontilhada é onde a abundância de hidrogênio muda (Hans-Christoph Thomas, 1967, Zeitschrift für Astrophysik, 67, 420).
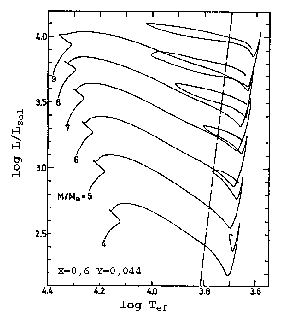
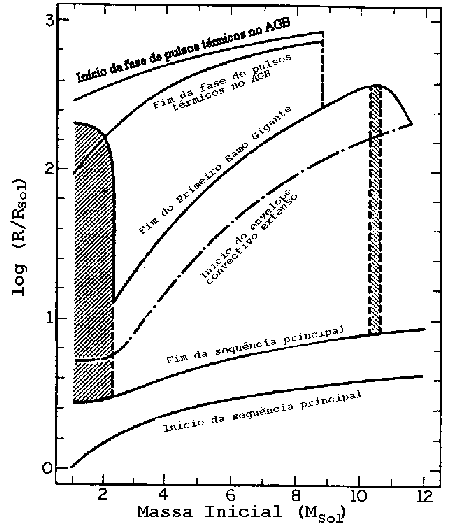 Diagrama H-R com as seqüências evolucionárias para massas
entre 4 e 9
Diagrama H-R com as seqüências evolucionárias para massas
entre 4 e 9 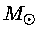 , desde a seqüência principal
até a fase de
queima nuclear de hélio. A linha pontilhada indica a borda vermelha
da faixa de instabilidade das Cefeidas
(B. Matraka,
C. Wassermann &
Alfred Weigert, 1982, Astronomy & Astrophysics, 107, 283 (direita) e
Variação do raio das estrelas com o tempo, devido
à sua evolução (esquerda).
, desde a seqüência principal
até a fase de
queima nuclear de hélio. A linha pontilhada indica a borda vermelha
da faixa de instabilidade das Cefeidas
(B. Matraka,
C. Wassermann &
Alfred Weigert, 1982, Astronomy & Astrophysics, 107, 283 (direita) e
Variação do raio das estrelas com o tempo, devido
à sua evolução (esquerda).
As estrelas de baixa massa são por definição aquelas
que desenvolvem um núcleo com elétrons degenerados logo
após sair da sequência principal. Elas têm um ramo gigante
mais estendido do que as estrelas de massa intermediária,
pois o núcleo exaurido de hidrogênio se esfria
por condução eletrônica quando os elétrons se
tornam degenerados, aumentando o tempo até o início
da queima de hélio, que termina a subida do ramo das gigantes.
Quando a massa do núcleo de hélio atinge cerca de
0,45  ,
um queima de hélio descontrolada se inicia no núcleo.
Esta queima descontrolada continua até que a degenerescência
seja levantada. A perda de energia por emissão de neutrinos
no núcleo causa um gradiente negativo de temperatura nas regiões
centrais do núcleo, e o início da queima de hélio
ocorre fora do centro e depois procede para dentro em uma
série de flashes que ocorrem sucessivamente mais próximos
do centro.
A luminosidade máxima devido a transformação de
,
um queima de hélio descontrolada se inicia no núcleo.
Esta queima descontrolada continua até que a degenerescência
seja levantada. A perda de energia por emissão de neutrinos
no núcleo causa um gradiente negativo de temperatura nas regiões
centrais do núcleo, e o início da queima de hélio
ocorre fora do centro e depois procede para dentro em uma
série de flashes que ocorrem sucessivamente mais próximos
do centro.
A luminosidade máxima devido a transformação de
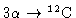 alcança
alcança
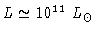 .
Esta energia não sai da estrela, mas permanece na camada
convectiva, que se estende quase até a camada de queima
de hidrogênio.
A temperatura sobe até que a degenerescência
desaparece. A proporcionalidade entre temperatura e
pressão então permite um novo equilíbrio:
o núcleo de hélio se expande e esfria, e
o modelo inicia uma fase de queima quiescente
de hélio, como os modelos de massa intermediária, que dura
cerca de
.
Esta energia não sai da estrela, mas permanece na camada
convectiva, que se estende quase até a camada de queima
de hidrogênio.
A temperatura sobe até que a degenerescência
desaparece. A proporcionalidade entre temperatura e
pressão então permite um novo equilíbrio:
o núcleo de hélio se expande e esfria, e
o modelo inicia uma fase de queima quiescente
de hélio, como os modelos de massa intermediária, que dura
cerca de 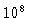 anos.
anos.
No Ramo Horizontal,
a posição do modelo no diagrama H-R
depende principalmente da metalicidade.
Os modelos de alta metalicidade se concentram em uma pequena região
no ramo das gigantes, chamado de Red clump,
aproximadamente 3 magnitudes abaixo
do topo do ramo gigante, enquanto que os modelos de baixa
metalicidade cobrem uma região extensa de temperaturas efetivas
mais azuis do que o ramo das gigantes, levando à designação
de ramo horizontal.
Com uma opacidade
K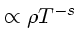 , podemos estimar
, podemos estimar
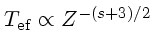 . Portanto, de Z=0,0001
(Pop II extrema) até Z=0,02, obtemos
. Portanto, de Z=0,0001
(Pop II extrema) até Z=0,02, obtemos
- Tef(Pop I)/Tef(Pop II)=0,64 para s=3 e
- Tef(Pop I)/Tef(Pop II)= 0,41 para s=0.
Os modelos têm aproximadamente a mesma luminosidade pois têm
aproximadamente a mesma massa nuclear e portanto a mesma
contribuição para a luminosidade pela queima do hélio.
Diferente dos modelos de massa intermediária, a contribuição
da camada queimando hidrogênio não é dominante para a
luminosidade. A massa do núcleo exaurido de hidrogênio no
fim do ramo horizontal é tipicamente
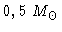 ,
ou seja,
,
ou seja,
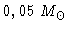 maior do que no início da queima do
hélio.
maior do que no início da queima do
hélio.
Após a exaustão do hélio central, o modelo
de baixa massa é similar ao modelo de massa intermediária:
um núcleo de C-O com elétrons degenerados, uma
camada extra-nuclear queimando hélio e um envelope
rico em hidrogênio em que o hidrogênio não
queima significativamente, mesmo na sua base. Os modelos
ocupam a mesma região do Ramo Gigante Assintótico (AGB).
Nesta fase a maior parte do envelope de hidrogênio
é perdido por vento radiativo.
Para massas acima de
8-9 ,
mas ainda abaixo de cerca de
10,5
,
mas ainda abaixo de cerca de
10,5 ,
o núcleo tem acima de 1
,
o núcleo tem acima de 1 e contém oxigênio, neônio e magnésio.
O núcleo é uma anã branca pré-fabricada, circundado por um envelope
com centenas de raios solares.
As estrelas do AGB são importantes no enriquecimento da galáxia e
dominantes na luminosidade integral de sistemas estelares de idades
intermediárias e, portanto, ferramentas para o estudo das populações
extragaláticas.
e contém oxigênio, neônio e magnésio.
O núcleo é uma anã branca pré-fabricada, circundado por um envelope
com centenas de raios solares.
As estrelas do AGB são importantes no enriquecimento da galáxia e
dominantes na luminosidade integral de sistemas estelares de idades
intermediárias e, portanto, ferramentas para o estudo das populações
extragaláticas.
Para os modelos de baixa massa, a fase inicial do AGB,
antes do início dos pulsos térmicos,
dura cerca de 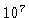 anos, comparados com
anos, comparados com 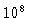 anos
no ramo gigante.
anos
no ramo gigante.
Para estrelas de População I, as observações
indicam que o AGB termina com massa de cerca de
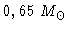 ,
ou seja, estrelas com massas iniciais de cerca de 1,4
,
ou seja, estrelas com massas iniciais de cerca de 1,4  aumentam a massa do núcleo em cerca de 0,15
aumentam a massa do núcleo em cerca de 0,15  durante
o AGB, e retornam aproximadamente metade de sua massa inicial
para o meio interestelar. A matéria perdida durante o
AGB é provavelmente enriquecida em carbono e elementos
ricos em nêutrons formados pelo processo "s".
durante
o AGB, e retornam aproximadamente metade de sua massa inicial
para o meio interestelar. A matéria perdida durante o
AGB é provavelmente enriquecida em carbono e elementos
ricos em nêutrons formados pelo processo "s".
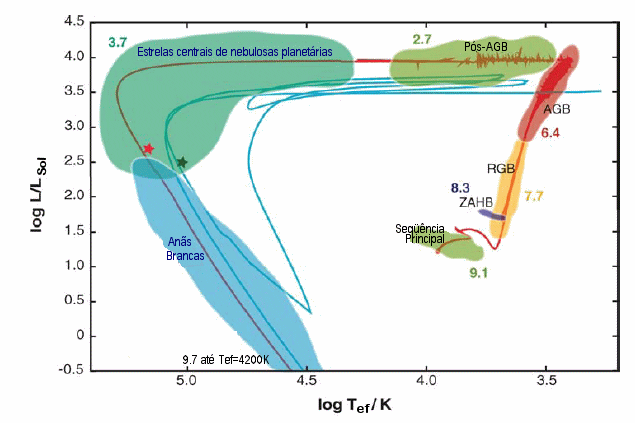 Modelo de uma estrela de
2
Modelo de uma estrela de
2  publicado por
Falk Herwig (2005, Annual Review of Astronomy and Astrophysics,
43, 435). Os números próximos às etapas correspondem ao log do
tempo que a estrela passa nesta etapa, em anos. A linha em azul,
correspondendo a fase de renascença após um pulso térmico
muito tardio, está deslocada de log T=-0.2 e log L=-0.5
para vizualização. Na fase de pós-AGB, há dificuldades de
convergência numérica nos modelos. O ZAHB (Zero Age
Horizontal Branch), ramo horizontal de idade zero
ocorre durante a queima de hélio no núcleo quiescente,
após a estrela ter subido ao topo do RGB (Red Giant
Branch), ramo das gigantes vermelhas. Nestes modelos,
se a estrela tem massa menor que 1,8 massas solares,
a ignição do He se dá em um núcleo degenerado.
Como as estrelas do AGB dominam a luminosidade dos
sistemas estelares de idade intermediária, elas são
importantes nos estudos dos sistemas extra-galáticos.
publicado por
Falk Herwig (2005, Annual Review of Astronomy and Astrophysics,
43, 435). Os números próximos às etapas correspondem ao log do
tempo que a estrela passa nesta etapa, em anos. A linha em azul,
correspondendo a fase de renascença após um pulso térmico
muito tardio, está deslocada de log T=-0.2 e log L=-0.5
para vizualização. Na fase de pós-AGB, há dificuldades de
convergência numérica nos modelos. O ZAHB (Zero Age
Horizontal Branch), ramo horizontal de idade zero
ocorre durante a queima de hélio no núcleo quiescente,
após a estrela ter subido ao topo do RGB (Red Giant
Branch), ramo das gigantes vermelhas. Nestes modelos,
se a estrela tem massa menor que 1,8 massas solares,
a ignição do He se dá em um núcleo degenerado.
Como as estrelas do AGB dominam a luminosidade dos
sistemas estelares de idade intermediária, elas são
importantes nos estudos dos sistemas extra-galáticos.
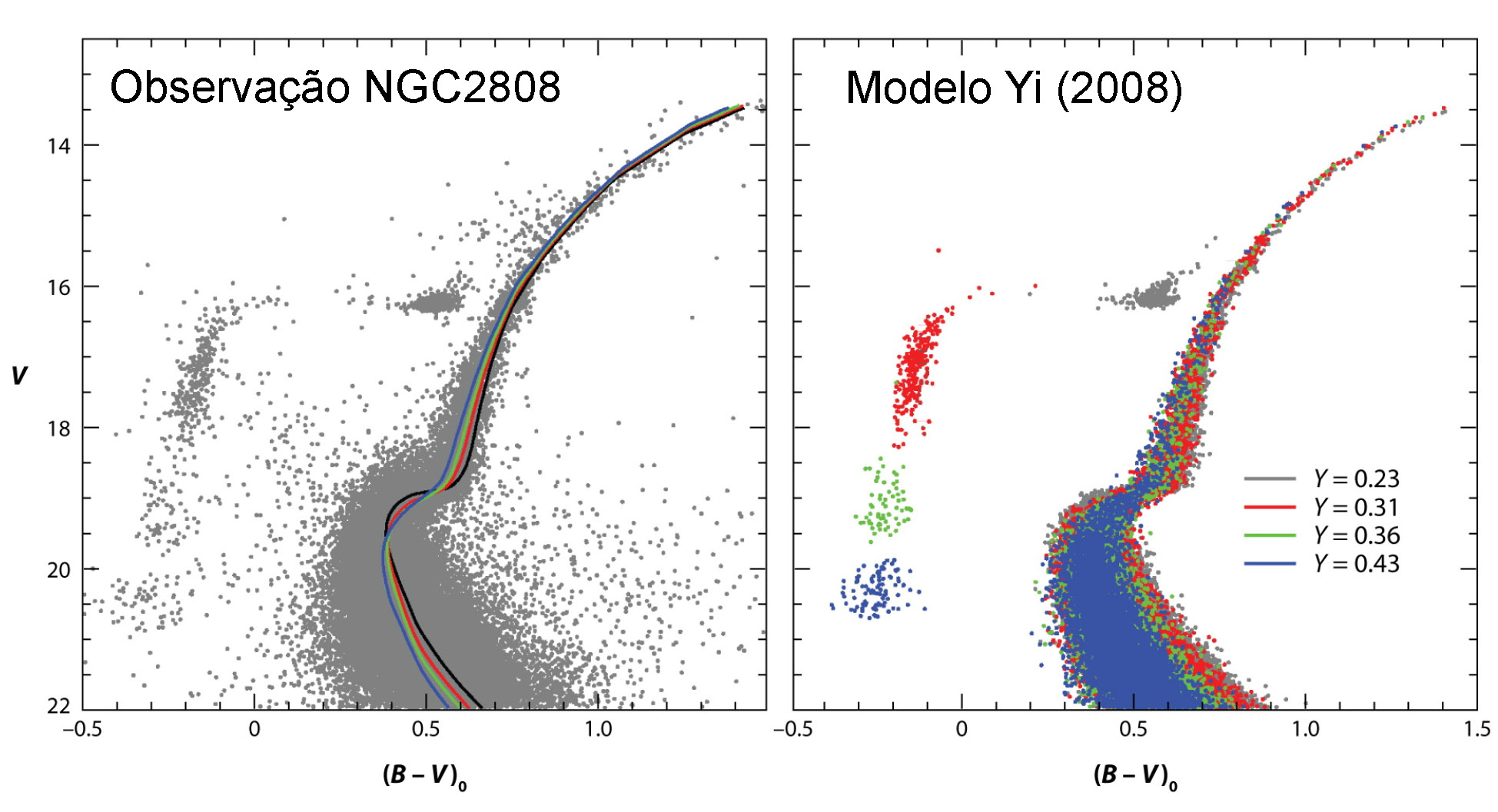
O aglomerado NGC 2808 apresenta múltiplas populações e o modelo calculado por
S.K. Yi (2008, Astronomical Society of the Pacific Conference Series, 392, Hot
Subdwarf Stars and Related Objects, editores Uli Heber, C. Simon Jeffery & Ralf Napiwotzki, 3)
consegue reproduzir as observações assumindo que as diferentes populações têm
a abundância de hélio variando de 0.23 a 0,43.
Já no topo do ramo gigante assintótico,
as estrelas se tornam variáveis tipo Mira,
com períodos de 6 meses a dois anos, e luminosidades da ordem
de 2500 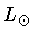 .
Para estrelas de massa abaixo de
7
.
Para estrelas de massa abaixo de
7 o forte esfriamento por emissão de neutrinos faz com que o
núcleo nunca atinja a temperatura necessária para
a ignição do carbono.
o forte esfriamento por emissão de neutrinos faz com que o
núcleo nunca atinja a temperatura necessária para
a ignição do carbono.
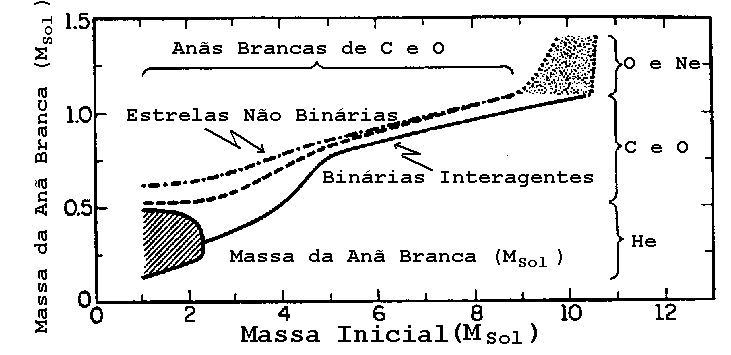 Relação entre a massa inicial da estrela e a composição
do núcleo da anã branca resultante, nos modelos de Icko Iben Jr.
Relação entre a massa inicial da estrela e a composição
do núcleo da anã branca resultante, nos modelos de Icko Iben Jr.
Adriano Pietrinferni, Santi Cassisi, Maurizio Salaris e Fiorella Castelli,
apresentam no
Astrophysical Journal (2006), 642, 797,
sua grade de modelos
entre 0,5 e 10 massas solares e
-2,6 < [Fe/H] < 0,05 para a população do halo e bojo.
Durante toda a evolução da estrela, a energia gravitacional
do núcleo vai aumentando, por contração, mas
no momento da explosão de uma supernova, aproximadamente
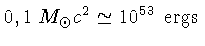 ,
correspondendo a toda a energia gravitacional acumulada, são
liberados, sendo que somente
,
correspondendo a toda a energia gravitacional acumulada, são
liberados, sendo que somente
 correspondem
à luminosidade perdida através de fótons. A maior parte
da energia é perdida através de neutrinos.
correspondem
à luminosidade perdida através de fótons. A maior parte
da energia é perdida através de neutrinos.
Em 1961 o japonês
Chushiro Hayashi (1920-2010)
demonstrou que uma estrela
totalmente convectiva
tem a menor temperatura
atmosférica possível;
modelos com temperaturas mais baixa não estão em equilíbrio
hidrostático. Esta temperatura é
chamada de limite de Hayashi, e corresponde ao ramo das gigantes
[Chushiro Hayashi & Reun Hoshi. The Outer Envelope of Giant Stars with Surface Convection Zone, Publications of the Astromical Society of Japan 13, 442-49 (1961)].
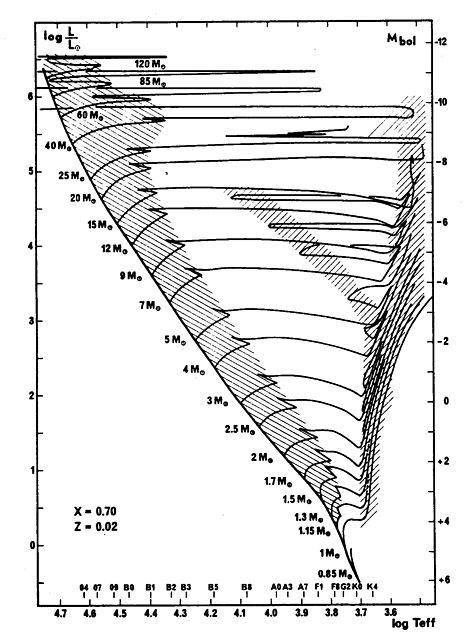 Diagrama HR teórico mostrando o caminho evolucionário de
estrelas de diferentes massas, com um overshooting
convectivo moderado,
conforme cálculos de André Maeder (1942-)
e Georges Meynet,
da Universidade de Genebra, publicados em
1989 no Astronomy & Astrophysics, 210, 155.
Nesses
modelos, a massa máxima de uma estrela Cefeida é de 12 massas solares.
A base de dados desses modelos pode ser encontrada na página do
Observatório Astronômico de Genebra.
As regiões sombreadas indicam a sequência principal (queima de H no núcleo)
e a região de queima de hélio no núcleo.
Diagrama HR teórico mostrando o caminho evolucionário de
estrelas de diferentes massas, com um overshooting
convectivo moderado,
conforme cálculos de André Maeder (1942-)
e Georges Meynet,
da Universidade de Genebra, publicados em
1989 no Astronomy & Astrophysics, 210, 155.
Nesses
modelos, a massa máxima de uma estrela Cefeida é de 12 massas solares.
A base de dados desses modelos pode ser encontrada na página do
Observatório Astronômico de Genebra.
As regiões sombreadas indicam a sequência principal (queima de H no núcleo)
e a região de queima de hélio no núcleo.
Programa para cálculo moderno e
resultados
Interface para as isócronas e síntese de populações estelares
Trilegal de Léo Girardi e Paola Marigo, de Pádova.
Achim Weiss
tem uma comparação dos modelos de evolução estelar de diversos grupos.
Nucleossíntese no AGB, pdf em Genebra.
Nucleosynthesis in Stars
and the Chemical Enrichment
of Galaxies, artigo de
Ken'ichi Nomoto,
Chiaki Kobayashi,
e Nozomu Tominaga
no Annual Review of Astronomy & Astrophysics, 2013, 51, 457-509.
The Formation and Early
Evolution of Low-Mass Stars and Brown Dwarfs,
Kevin L. Luhman, no Annual Review of Astronomy & Astrophysysics, 2012,
50, 65-106.
Presupernova Evolution
of Massive Single and Binary Stars,
Norbert Langer
no Annual Review of Astronomy & Astrophysics, 2012,
50, 107-164.



Volta: Interiores Estelares
Anterior: Estrelas Completamente Convectivas
Próxima: Modelos de Alta Massa
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 26 jun 2016
![]() ,
,
![]() e
e
![]() ,
além da condição de equilíbrio radiativo
,
além da condição de equilíbrio radiativo
![]() , em uma série de pontos no intervalo começando
em
, em uma série de pontos no intervalo começando
em ![]() e terminando em
e terminando em ![]() , onde
, onde ![]() é a variável independente
e
é a variável independente
e ![]() é chamado de passo. Estas derivadas são então utilizadas
para encontrar
é chamado de passo. Estas derivadas são então utilizadas
para encontrar ![]() . As versões mais sofisticadas do método
automaticamente ajustam o valor do passo para manter a precisão
desejada.
. As versões mais sofisticadas do método
automaticamente ajustam o valor do passo para manter a precisão
desejada.
![]() , onde
, onde ![]() é o ponto de ajuste, de modo que podemos calcular a derivada
desta diferença, que deve se anular no ponto de mínimo.
Como nossas funções não são lineares, iteramos o
cálculo até que a diferença esteja dentro da precisão
pré-determinada. Este método, de transformar um problema
não linear em um linear, chama-se de método de
Newton-Raphson
[Isaac Newton (1642-1727) e Joseph Raphson (1648-1715)].
No método de Henyey, a cada iteração correções para todas as
variáveis em todos os pontos são calculados simultaneamente
[Louis George Henyey (1910-1970),
J.E. Forbes e Nancy L. Gould 1964, Astrophysical Journal, 139, 306].
Nosso cálculo para estrelas esféricas consiste então em um sistema
de 4 equações diferenciais ordinárias para as 4 variáveis: r, P, T e L.
Como linearizamos as equações assumindo correções pequenas,
se a aproximação inicial é muito diferente da solução,
as correções necessárias são grandes e o sistema não converge.
é o ponto de ajuste, de modo que podemos calcular a derivada
desta diferença, que deve se anular no ponto de mínimo.
Como nossas funções não são lineares, iteramos o
cálculo até que a diferença esteja dentro da precisão
pré-determinada. Este método, de transformar um problema
não linear em um linear, chama-se de método de
Newton-Raphson
[Isaac Newton (1642-1727) e Joseph Raphson (1648-1715)].
No método de Henyey, a cada iteração correções para todas as
variáveis em todos os pontos são calculados simultaneamente
[Louis George Henyey (1910-1970),
J.E. Forbes e Nancy L. Gould 1964, Astrophysical Journal, 139, 306].
Nosso cálculo para estrelas esféricas consiste então em um sistema
de 4 equações diferenciais ordinárias para as 4 variáveis: r, P, T e L.
Como linearizamos as equações assumindo correções pequenas,
se a aproximação inicial é muito diferente da solução,
as correções necessárias são grandes e o sistema não converge.
![]() só depende do conhecimento
do estado em tempo
só depende do conhecimento
do estado em tempo ![]() . Este método assume que os movimentos
são subsônicos, isto é, que choques não se desenvolvem.
. Este método assume que os movimentos
são subsônicos, isto é, que choques não se desenvolvem.


 Foto de Icko Iben Jr. (1931-), que estudou com
Martin Schwarzschild (1912-1997), o precursor dos
cálculos de modelos de evolução estelar. Icko Iben
continuou este trabalho e é considerado o maior especialista
no assunto.
Foto de Icko Iben Jr. (1931-), que estudou com
Martin Schwarzschild (1912-1997), o precursor dos
cálculos de modelos de evolução estelar. Icko Iben
continuou este trabalho e é considerado o maior especialista
no assunto.
![]() e encontraram
e encontraram
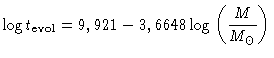




![]() a conversão de
hidrogênio em hélio se dá pelo ciclo CNO, em um núcleo
convectivo, se a estrela possui carbono.
Depois de consumir o hidrogênio central, a estrela
se desloca rapidamente para o ramo das gigantes, queimando hidrogênio
em uma camada fina sobre o núcleo em rápida contração e
aquecimento, composto essencialmente de hélio puro.
Como a camada é fina, a temperatura em que ocorre a queima é
significativamente maior do que quando houve queima no núcleo,
já que a mesma luminosidade tem que ser gerada em uma camada com
menor massa.
Com a contração do núcleo, há expansão
das camadas externas.
Ao se
aproximar do ramo das gigantes, a base da região
convectiva superficial se extende até as camadas em que
o carbono foi convertido em nitrogênio; a abundância
superficial destes dois elementos começa a mudar em
quantidades detectáveis. Este processo de mistura
convectiva de elementos processados termonuclearmente
no núcleo convectivo é chamado de primeira dragagem
( first dredge-up).
a conversão de
hidrogênio em hélio se dá pelo ciclo CNO, em um núcleo
convectivo, se a estrela possui carbono.
Depois de consumir o hidrogênio central, a estrela
se desloca rapidamente para o ramo das gigantes, queimando hidrogênio
em uma camada fina sobre o núcleo em rápida contração e
aquecimento, composto essencialmente de hélio puro.
Como a camada é fina, a temperatura em que ocorre a queima é
significativamente maior do que quando houve queima no núcleo,
já que a mesma luminosidade tem que ser gerada em uma camada com
menor massa.
Com a contração do núcleo, há expansão
das camadas externas.
Ao se
aproximar do ramo das gigantes, a base da região
convectiva superficial se extende até as camadas em que
o carbono foi convertido em nitrogênio; a abundância
superficial destes dois elementos começa a mudar em
quantidades detectáveis. Este processo de mistura
convectiva de elementos processados termonuclearmente
no núcleo convectivo é chamado de primeira dragagem
( first dredge-up).
![]() (ou acima de 1,8
(ou acima de 1,8 ![]() se overshooting for significativo),
a temperatura central atingirá
se overshooting for significativo),
a temperatura central atingirá
![]() K e a densidade central
K e a densidade central
![]() em um núcleo não degenerado, e o
hélio começará a ser transformado em carbono no centro,
revertendo a ascensão da estrela no ramo das gigantes
no diagrama H-R.
A liberação de energia expande o núcleo
e as camadas externas se contraem, aumentando
a temperatura efetiva de cerca de 4000 K para 8000 K.
A estrela então passará uma longa fase
de queima de hélio em um núcleo convectivo e em crescimento.
A queima de hidrogênio em uma camada fina continua a
prover a maior parte da luminosidade da estrela (80%) e, portanto,
a massa da região central exaurida de hidrogênio continua
a aumentar.
Alfred Gautschy (2012)
faz um resumo da ignição de hélio fora do centro em um gás degenerado
para estrelas até 2 massas solares. A ignição fora de centro, causada
pela forte emissão de neutrinos no centro, foi primeiro estudada por
Hans-Christoph Thomas em 1967, no
Zeitschrift für Astrophysik, 67, 420.
em um núcleo não degenerado, e o
hélio começará a ser transformado em carbono no centro,
revertendo a ascensão da estrela no ramo das gigantes
no diagrama H-R.
A liberação de energia expande o núcleo
e as camadas externas se contraem, aumentando
a temperatura efetiva de cerca de 4000 K para 8000 K.
A estrela então passará uma longa fase
de queima de hélio em um núcleo convectivo e em crescimento.
A queima de hidrogênio em uma camada fina continua a
prover a maior parte da luminosidade da estrela (80%) e, portanto,
a massa da região central exaurida de hidrogênio continua
a aumentar.
Alfred Gautschy (2012)
faz um resumo da ignição de hélio fora do centro em um gás degenerado
para estrelas até 2 massas solares. A ignição fora de centro, causada
pela forte emissão de neutrinos no centro, foi primeiro estudada por
Hans-Christoph Thomas em 1967, no
Zeitschrift für Astrophysik, 67, 420.


![]() ,
logo após o início da segunda dragagem a matéria
no núcleo exaurido de hélio atinge
,
logo após o início da segunda dragagem a matéria
no núcleo exaurido de hélio atinge
![]() e os elétrons se tornam degenerados. Nestas condições,
a condução de calor pelos elétrons ajuda a manter a
matéria nuclear dentro de um fator de 2 da temperatura média
do núcleo,
e os elétrons se tornam degenerados. Nestas condições,
a condução de calor pelos elétrons ajuda a manter a
matéria nuclear dentro de um fator de 2 da temperatura média
do núcleo,
![]() K,
e a perda de energia pelos processos de plasma
e foto-neutrinos se tornam importantes. Grande parte da liberação
de energia gravitacional potencial pelas camadas superiores
é perdida pela emissão de neutrinos, mantendo a temperatura
do núcleo próxima da temperatura da camada onde ocorre
a queima de hélio. O núcleo da estrela tem as dimensões
de uma anã branca, e é de fato uma anã branca quente.
K,
e a perda de energia pelos processos de plasma
e foto-neutrinos se tornam importantes. Grande parte da liberação
de energia gravitacional potencial pelas camadas superiores
é perdida pela emissão de neutrinos, mantendo a temperatura
do núcleo próxima da temperatura da camada onde ocorre
a queima de hélio. O núcleo da estrela tem as dimensões
de uma anã branca, e é de fato uma anã branca quente.


![]() ,
o limite de Chandrasekhar. Neste ponto o carbono começa a queimar,
pois há forte escudamento eletrônico,
e depois de um curto episódio durante o qual a
perda de energia pelo processo Urca balança a energia
gerada pela queima do carbono, a taxa de queima
de carbono cresce exponencialmente, criando uma frente que queima
que se desloca na direção da superfície,
convertendo matéria em elementos do grupo do ferro,
mas com velocidades acima da velocidade de escape.
Desta forma, o núcleo é completamente desfeito
como uma supernova.
Nos modelos com maior perda de massa, o início da queima do
C ocorre antes do núcleo atingir a massa de Chandrasekhar.
A massa do envelope rico em hidrogênio do modelo de supernova é grande
o suficiente para que linhas de hidrogênio sejam proeminentes.
Estas são as SN II.
,
o limite de Chandrasekhar. Neste ponto o carbono começa a queimar,
pois há forte escudamento eletrônico,
e depois de um curto episódio durante o qual a
perda de energia pelo processo Urca balança a energia
gerada pela queima do carbono, a taxa de queima
de carbono cresce exponencialmente, criando uma frente que queima
que se desloca na direção da superfície,
convertendo matéria em elementos do grupo do ferro,
mas com velocidades acima da velocidade de escape.
Desta forma, o núcleo é completamente desfeito
como uma supernova.
Nos modelos com maior perda de massa, o início da queima do
C ocorre antes do núcleo atingir a massa de Chandrasekhar.
A massa do envelope rico em hidrogênio do modelo de supernova é grande
o suficiente para que linhas de hidrogênio sejam proeminentes.
Estas são as SN II.
![]() ,
de acordo com a função de massa proposta em 1955 pelo
astrônomo americano
Edwin Ernest Salpeter (1925-2008)
que dá a taxa de formação de estrelas por
,
de acordo com a função de massa proposta em 1955 pelo
astrônomo americano
Edwin Ernest Salpeter (1925-2008)
que dá a taxa de formação de estrelas por
![]() por ano
por ano
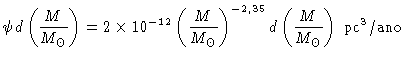
![]() .
Philipp Podsiadlowski et al. 2004, Astrophysical Journal, 612, 1044 estimam
11±1
.
Philipp Podsiadlowski et al. 2004, Astrophysical Journal, 612, 1044 estimam
11±1 ![]() como o limite inferior para a massa das estrelas
que geram estrelas de nêutrons.
Stephen J. Smartt, no seu artigo
Progenitors of Core-Collapse Supernovae, de
2009 no Annual Review of Astronomy & Astrophysics, 47, 63,
e com
J. J. Eldridge, R. M. Crockett, & J. R.Maund, no
The death of massive stars - I. Observational constraints on the progenitors of Type II-P supernovae,
publicado em 2009 no Monthly Notices of the Royal Astronomical Sociery, 395, 1409,
concluem que estrelas com massa superior a 8,5±1,5 MSol
tornam-se supernovas tipo II.
como o limite inferior para a massa das estrelas
que geram estrelas de nêutrons.
Stephen J. Smartt, no seu artigo
Progenitors of Core-Collapse Supernovae, de
2009 no Annual Review of Astronomy & Astrophysics, 47, 63,
e com
J. J. Eldridge, R. M. Crockett, & J. R.Maund, no
The death of massive stars - I. Observational constraints on the progenitors of Type II-P supernovae,
publicado em 2009 no Monthly Notices of the Royal Astronomical Sociery, 395, 1409,
concluem que estrelas com massa superior a 8,5±1,5 MSol
tornam-se supernovas tipo II.


 O ramo horizontal é onde as estrelas queimam He no núcleo. As estrelas
com massa até cerca de 3
O ramo horizontal é onde as estrelas queimam He no núcleo. As estrelas
com massa até cerca de 3 ![]() chegam ao ramo horizontal
com um núcleo com aproximadamente 0,6
chegam ao ramo horizontal
com um núcleo com aproximadamente 0,6 ![]() .
Nos modelos de
Young-Wook Lee, Pirre Demarque e Robert Zinn, mostrados na figura ao lado e publicados no artigo The Horizontal-Branch Stars in Globular Clusters. II. The Second Parameter Phenomenon em 1994, no Astrophysical Journal,
423, 248, eles mostram que a diferença na idade e na metalicidade dos
aglomerados explica a variedade de ramos horizontais observados.
.
Nos modelos de
Young-Wook Lee, Pirre Demarque e Robert Zinn, mostrados na figura ao lado e publicados no artigo The Horizontal-Branch Stars in Globular Clusters. II. The Second Parameter Phenomenon em 1994, no Astrophysical Journal,
423, 248, eles mostram que a diferença na idade e na metalicidade dos
aglomerados explica a variedade de ramos horizontais observados.







![]() , podemos estimar
, podemos estimar
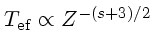 . Portanto, de Z=0,0001
(Pop II extrema) até Z=0,02, obtemos
. Portanto, de Z=0,0001
(Pop II extrema) até Z=0,02, obtemos
![]() ,
ou seja,
,
ou seja,
![]() maior do que no início da queima do
hélio.
maior do que no início da queima do
hélio.
![]() ,
mas ainda abaixo de cerca de
10,5
,
mas ainda abaixo de cerca de
10,5![]() ,
o núcleo tem acima de 1
,
o núcleo tem acima de 1![]() e contém oxigênio, neônio e magnésio.
O núcleo é uma anã branca pré-fabricada, circundado por um envelope
com centenas de raios solares.
As estrelas do AGB são importantes no enriquecimento da galáxia e
dominantes na luminosidade integral de sistemas estelares de idades
intermediárias e, portanto, ferramentas para o estudo das populações
extragaláticas.
e contém oxigênio, neônio e magnésio.
O núcleo é uma anã branca pré-fabricada, circundado por um envelope
com centenas de raios solares.
As estrelas do AGB são importantes no enriquecimento da galáxia e
dominantes na luminosidade integral de sistemas estelares de idades
intermediárias e, portanto, ferramentas para o estudo das populações
extragaláticas.
![]() anos, comparados com
anos, comparados com ![]() anos
no ramo gigante.
anos
no ramo gigante.
![]() ,
ou seja, estrelas com massas iniciais de cerca de 1,4
,
ou seja, estrelas com massas iniciais de cerca de 1,4 ![]() aumentam a massa do núcleo em cerca de 0,15
aumentam a massa do núcleo em cerca de 0,15 ![]() durante
o AGB, e retornam aproximadamente metade de sua massa inicial
para o meio interestelar. A matéria perdida durante o
AGB é provavelmente enriquecida em carbono e elementos
ricos em nêutrons formados pelo processo "s".
durante
o AGB, e retornam aproximadamente metade de sua massa inicial
para o meio interestelar. A matéria perdida durante o
AGB é provavelmente enriquecida em carbono e elementos
ricos em nêutrons formados pelo processo "s".



![]() ,
correspondendo a toda a energia gravitacional acumulada, são
liberados, sendo que somente
,
correspondendo a toda a energia gravitacional acumulada, são
liberados, sendo que somente
![]() correspondem
à luminosidade perdida através de fótons. A maior parte
da energia é perdida através de neutrinos.
correspondem
à luminosidade perdida através de fótons. A maior parte
da energia é perdida através de neutrinos.

![]()