Tempo de vida das estrelas

O tempo de vida de uma estrela é a razão entre a energia que ela tem disponível e a taxa com que ela gasta essa energia, ou seja, sua luminosidade. Como a luminosidade da estrela na sequência principal é tanto maior quanto maior é a sua massa ($L\propto M^3$), resulta que o tempo de vida é controlado pela massa da estrela: quanto mais massiva a estrela, mais rapidamente ela gasta sua energia, e menos tempo ela dura.

A parte mais longa da vida da estrela é quando ela está na sequência principal, gerando energia através de fusões termonucleares de hidrogênio em hélio. Em estrelas como o Sol, as reações mais importantes são as que produzem, como resultado líquido, a transformação de quatro núcleos de hidrogênio (quatro prótons) em um núcleo de hélio (partícula α). Nessa transformação, existe uma diferença de massa entre a massa que entrou na reação - maior - e a massa que saiu - menor -. Essa massa "desaparecida" é transformada em energia pela equação de Einstein: E = mc².

$$4m_p (4,0324\, {\rm u} ) \longrightarrow 1m_{\alpha} (4,0039\, {\rm u})$$

onde u = unidade de massa atômica = $1,66 \times 10^{-27}$ kg.

A diferença de massa é:

Dividindo-se pela massa inicial:

Portanto 0,7% = 7 milésimos da massa que entra na reação é transformada em energia. A massa que entra nessa reação é apenas a massa que se encontra no núcleo da estrela, pois apenas no núcleo a estrela atinge temperaturas suficientemente altas - ≥8 milhões K - para permitir as reações termonucleares. A massa da estrela contida em seu núcleo é 10% da massa total da estrela. Isso significa que, de toda a massa da estrela, apenas 10% contribui para a geração de energia durante a maior parte de sua vida, a parte em que ela está na sequência principal. Este é o limite de Schenberg-Chandrasekhar, publicado em 1942 pelo brasileiro Mário Schenberg (1914-1990)

Mário Schenberg

e pelo indiano Subrahmanyan Chandrasekhar (1910-1995) (Astrophysical Journal, 96, 161) e corresponde ao ponto da evolução de uma estrela em que o balanço de pressão no núcleo isotérmico não pode ser mais alcançado.

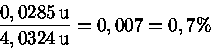
Portanto, a energia disponível nessa etapa é:

onde $E_{SP}$ significa energia na sequência principal.

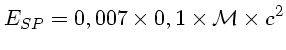
No caso do Sol essa energia vale:

$$E_{SP}^\odot = 0,007 \times 0,1 \times M_\odot \times c^2$$

$$= 0,007 \times 0,1 \times 1,99 \times 10^{30} kg \times ({3 \times 10^8 m/s)^2}$$

$$= 1,26 \times 10^{44} J$$

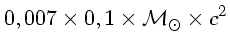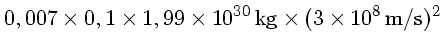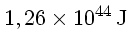O tempo de vida do Sol na sequência principal é igual à energia nuclear disponível dividida pela luminosidade do Sol na sequência principal, já que a luminosidade é a quantidade de energia perdida por unidade de tempo:

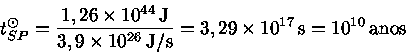
Para uma estrela qualquer, o tempo de vida na sequência principal t_SP = τ_SP pode ser calculado em termos do tempo de vida do Sol na mesma fase:

logo

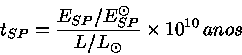
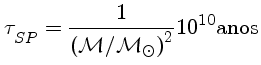
Exercício:

Demonstre que o tempo de vida na sequência principal para uma estrela cuja massa é 0,85 M$_\odot$ é igual à idade do Universo, de 13,7 bilhões de anos. Para calcular a luminosidade, use a relação massa-luminosidade $L\propto M^3$.

Próxima: Escalas de tempo evolutivo Anterior: Fusão Termo-Nuclear