

Próxima: Populações Estelares
Volta: Nossa Galáxia: a Via Láctea
Anterior: Movimento das Estrelas
O Sol, as outras estrelas, as nebulosas gasosas, e tudo o que faz parte
da galáxia, gira em torno do centro galáctico movido pela atração
gravitacional da grande quantidade de estrelas (massa) ali concentradas, da mesma
forma que os planetas giram em torno do Sol.
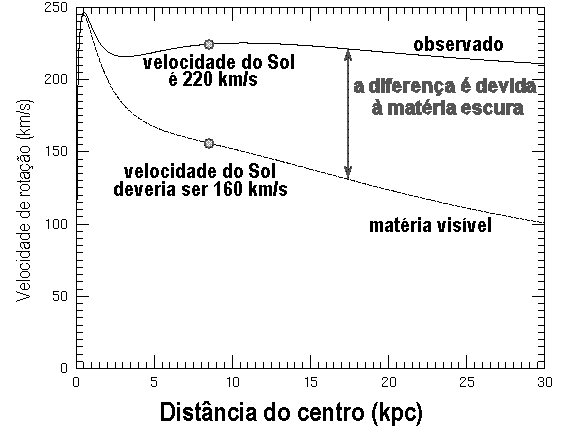
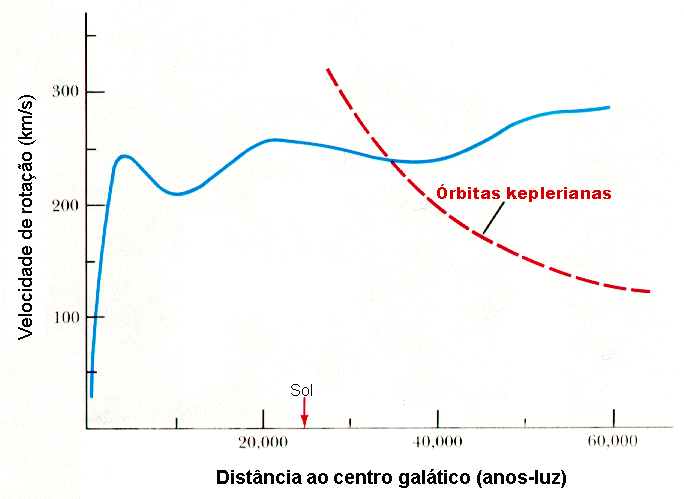 A curva azul mostra a velocidade de rotação
observada na Via Láctea, enquanto a curva pontilhada vermelha a
curva esperada se a massa estivesse concentrada onde
a luz está.
A curva azul mostra a velocidade de rotação
observada na Via Láctea, enquanto a curva pontilhada vermelha a
curva esperada se a massa estivesse concentrada onde
a luz está.
Observando o movimento de rotação
de uma estrela na periferia da galáxia, podemos determinar aproximadamente
a massa da Galáxia, MG,
desde que saibamos a distância dessa estrela ao
centro galáctico. Tomemos como exemplo o próprio Sol, e vamos
assumir que ele está em uma órbita circular em torno do centro galático
com velocidade v⊙.
A força centrípeta sofrida pelo Sol é
que é produzida pela atração gravitacional entre o Sol e
a massa da Galáxia interna ao Sol,
dada por (m=M⊙):
O Primeiro Teorema de Newton
estabelece que um corpo dentro de uma casca esférica de matéria
não experimenta qualquer força gravitacional desta casca. Na relatividade geral o teorema
equivalente chama-se Teorema de Birkhoff
[George David Birkhoff (1884-1944)]. Isto pode ser compreendido porque os ângulos
sólidos que se estendem de um ponto dentro da esfera para direções opostas têm áreas
que escalam com r2, enquanto a força gravitacional escala com r-2,
de modo que as forças gravitacionais das áreas opostas se cancelam exatamente.
Obtenção da curva de rotação
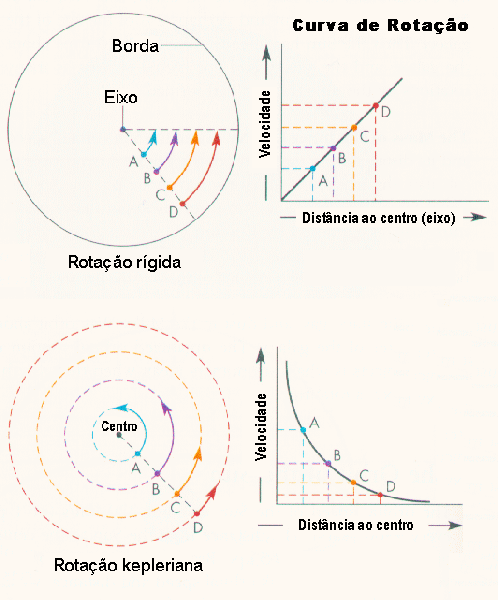
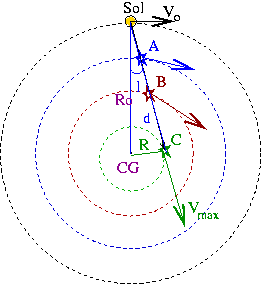
Para entender como é obtida a curva de rotação vamos considerar a
figura abaixo, onde os quatro círculos concêntricos representam
quatro órbitas estelares no disco da Galáxia, assumidas circulares por
simplicidade. A órbita mais externa no gráfico
é ocupada pelo Sol. Devido à rotação diferencial, as velocidades
das estrelas em órbitas mais internas são maiores do que as das estrelas em órbitas
mais externas (movimento kepleriano). Assim, a velocidade do Sol (V⊙) é
menor do que a velocidade da estrela A, que é menor do que a velocidade da
estrela B, que é menor do que a velocidade da estrela C.
Para uma certa longitude galáctica l,
a componente radial da velocidade de
cada estrela, medida a partir do Sol, aumenta à medida que diminui a distância
galactocêntrica da estrela, de forma
que quando a velocidade radial for máxima a distância galactocêntrica
é mínima para as estrelas a essa longitude.
Nessa situação, temos que R, a distância da estrela ao centro da Galáxia, é dada
por
onde R⊙ é a distância do Sol ao centro galáctico.
A velocidade da estrela nesse ponto, relativa ao Sol, será
Assumindo que V⊙ e R⊙ são conhecidos, então podemos construir a
curva V × R. Os valores aproximados para V⊙ e R⊙ são, respectivamente,
229 km/s e 8,2 kpc.
Na verdade, as curvas de rotação da Galáxia não são obtidas a partir
de observações de estrelas, e sim a partir de observações do gás
hidrogênio neutro (HI), uma vez que a radiação emitida por esse gás,
estando na região espectral de rádio, atravessa bem a poeira do disco
galáctico. Atualmente também está sendo usada a emissão de moléculas
de dióxido de carbono (CO) com esse mesmo objetivo.
O raciocínio seguido é o mesmo descrito para o caso de estrelas.
Os estudos da rotação
galática mostram que nas proximidades do Sol a velocidade de rotação
é de V⊙=229 km/s. Sabemos que a distância do Sol ao centro galáctico é
de 8,2 kpc = 2,5 × 1020 m.
A massa da galáxia MG, interna ao Sol,
pode então ser calculada:
M
G⊙=
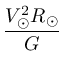
=
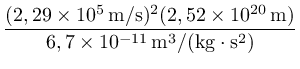
MG⊙=1,97×1041 kg ≃ 1011M⊙
Portanto, considerando o Sol como uma estrela de massa típica,
a Via Láctea tem aproximadamente 100 bilhões de estrelas.
Este é um limite inferior, pois estamos considerando apenas
a massa interna à orbita do Sol.
A curva de rotação da Galáxia
A massa da Galáxia, calculada da maneira acima, é apenas a massa contida
dentro da órbita do Sol em torno do centro Galáctico.
Para conhecer a massa existente além da órbita do Sol, é necessário
medir o movimento de estrelas e do gás localizados a distâncias maiores
do centro Galáctico do que o Sol.
Através de observações em rádio,
os astrônomos mediram o movimento do gás no disco,
até distâncias além do limite visível da Galáxia, e determinaram,
assim, a curva de rotação da Galáxia, que é a
velocidade de rotação em função da distância ao centro.
Quando usamos essa curva
para calcular a massa até uma distância de
15 kpc - quase duas vêzes
a distância do Sol ao centro galáctico -
vemos que a massa contida
dentro desse raio
é de 2 ×1011 MSol,
ou seja, o dobro da massa contida dentro da órbita do Sol.
A distância de 15 kpc corresponde ao limite da estrutura espiral visível
da Galáxia (onde visível, aqui, significa o que pode ser detectado
em qualquer comprimento de onda). Portanto, era de se esperar que, a
partir desse ponto, a curva de rotação passasse a decrescer,
pois se a maior parte da massa da Galáxia estivesse contida até esse
raio, o movimento das estrelas e do gás situados mais distantes deveria
ser cada vez mais lento, da mesma forma que a velocidade dos planetas
diminui à medida que aumenta sua distância ao Sol. Supreendentemente,
não é isso o que se observa. Pelo contrário,
a curva de rotação
aumenta ligeiramente para distâncias maiores, o que
implica que a quantidade de massa continua a crescer.
A velocidade
de rotação, à distância de 40 kpc, corresponde a uma massa
de 6 ×1011 MSol, o que
só pode ser explicado considerando que
nossa Galáxia contém matéria
não-visível que se estende muito além da matéria
visível, e que constitui, no mínimo, dois terços da massa
total
da Galáxia. Esta é uma indicação de um problema
muito maior, chamado de
matéria escura (invisível, que não emite luz),
externa à órbita do Sol.
 Essa massa, que só interage pela gravidade,
ainda não foi detectada em laboratório e constitui um dos
pontos mais perplexantes da astronomia moderna. Está
distribuída em um halo extenso em torno da Galáxia. Conclusão: a curva
de rotação observada prova que existe matéria escura em nossa Galáxia
e que ela é dominante.
Essa massa, que só interage pela gravidade,
ainda não foi detectada em laboratório e constitui um dos
pontos mais perplexantes da astronomia moderna. Está
distribuída em um halo extenso em torno da Galáxia. Conclusão: a curva
de rotação observada prova que existe matéria escura em nossa Galáxia
e que ela é dominante.
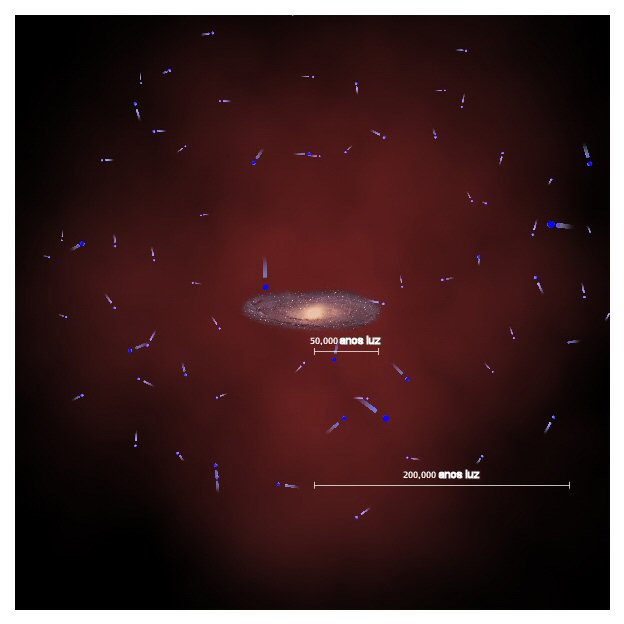
 Em 2008, o astrônomo chinês Xiangxiang Xue liderou um grupo de astrônomos
(Hans-Walter Rix, G. Zhao, Paola Re Fiorentin, Thorsten Naab, Matthias Steinmetz, Frank C. van den Bosch, Timoth C. Beers, Young Sun Lee, Eric F. Bell, C. Rockosi, B. Yanny, Heide Newberg, R. Wilhelm, X. Kang, M. C. Smith, D. P. Schneider) no
estudo de 2401 estrelas azuis brilhantes (do ramo horizontal) distribuídas a até 60 kpc do
centro de nossa Galáxia, com o
Sloan Digital Sky Survey, para medir a massa da Via Láctea,
publicando no Astrophysical Journal, 684, 1143,
M(<60 kpc) = (4,0±0,7)×1011MSol,
com o qual estimam a massa virial do halo de matéria escura como
M = (1,0±0,3)×1012MSol.
Em 2008, o astrônomo chinês Xiangxiang Xue liderou um grupo de astrônomos
(Hans-Walter Rix, G. Zhao, Paola Re Fiorentin, Thorsten Naab, Matthias Steinmetz, Frank C. van den Bosch, Timoth C. Beers, Young Sun Lee, Eric F. Bell, C. Rockosi, B. Yanny, Heide Newberg, R. Wilhelm, X. Kang, M. C. Smith, D. P. Schneider) no
estudo de 2401 estrelas azuis brilhantes (do ramo horizontal) distribuídas a até 60 kpc do
centro de nossa Galáxia, com o
Sloan Digital Sky Survey, para medir a massa da Via Láctea,
publicando no Astrophysical Journal, 684, 1143,
M(<60 kpc) = (4,0±0,7)×1011MSol,
com o qual estimam a massa virial do halo de matéria escura como
M = (1,0±0,3)×1012MSol.
Em 2014, Tilmann Piffl e colaboradores do RAdial Velocity Experiment (RAVE) publicaram no Astronomy & Astrophysics, 562, id.A91
a determinação de MG=(1,6±0,5)×1012MSol como a massa total (barions e matéria escura),
integrando até 200 vezes a densidade da energia da radiação de fundo,
e uma velocidade de escape da Galáxia de 533±54 km/s.

Imagem da Via Láctea e Nuvens de Magalhães (abaixo da Via Lácte) obtida com um mosaico das imagens do satélite Gaia.
Mas Gaia DR3 estima a massa total da Via Láctea em 2×1011 (200 bilhões) de massas solares, muito menor do que o trilhão estimado anteriormente. A massa escura é so duas vezes a massa luminosa.
Determinações da distância ao centro da Galáxia
R0 = 8178 ± 13estat. ±22sis. pc,
Gravity Collaboration (2019), Astronomy & Astrophysics, 625, L10.
R0 = 8,32 ± 0,07estat. ±0,14sis. kpc,
MBN=4.28 ± 0.10estatístico ± 0.21sistemático × 106 MSol, 2016, para a distância ao buraco negro Sagitarius A*,
An Update on Monitoring Stellar Orbits in the Galactic Center,
Stefan Gillessen, Phillipp Plewa, Frank Eisenhauer, Re'em Sari, Idel Waisberg, Maryam Habibi, Oliver Pfuhl, Elizabeth George, Jason
Dexter, Sebastiano von Fellenberg, Thomas Ott, Reinhard Genzel.
R0 = 7,86±0,14±0,04 kpc para a distância ao buraco negro no centro da Galáxia (An Improved Distance and Mass Estimate for Sgr A* from a Multistar Orbit Analysis,
Anna Boehle, Andrea M. Ghez, R. Schödel, L. Meyer, S. Yelda, S. Albers, G. D. Martinez, E. E. Becklin, T. Do, J. R. Lu, K. Matthews, M. R. Morris, B. Sitarski, G. Witzel,
2016, Astrophysical Journal, 830, 17B), e MBN=(4,02±0,16±0,04)×106 massas solares.
e
R0=8,53-0,150,21,
The Nuclear Cluster of the Milky Way: Total Mass and Luminosity,
Tobias K. Fritz, Sotiris Chatzopoulos, Ortwin Gerhard, Stefan Gillessen, Reinhard Genzel, Oliver Pfuhl, Sandro Tacchella, Frank Eisenhauer, Thomas Ott, 2016,
Astrophysical Journal, 821, Issue 1, article id. 44..
R0= 8,2±0,34 para a distância ao centro da Galáxia [Stefan Gillessen et al. 2013. in IAU Symp. 289,
Advancing the Physics of Cosmic Distances, ed. Richard de Grijs (Cambridge,
UK: Cambridge Univ. Press), 29].
R0= 8,3±0,6 para a distância ao centro da Galáxia e
v0 = 254 ± 16 km/s para a velocidade do sistema local de repouso (Andrea M. Ghez et al. 2008, Astrophysical Journal, 689, 1044;
Stefan Gillessen et al. 2009, Astrophysical Journal, 707, L114; Mark Jonathan Reid et al. 2009, Astrophysical Journal, 700, 137 e Astrophysical Journal, 705, 1548).
R0 =7,9±0,8 kpc considerando a paralaxe do maser de água, Mark Jonathan Reid et al. 2009, Astrophysical Journal, 700, 137 e Astrophysical Journal, 705, 1548.
R0 =8,2±0,4 kpc, Noriyuki Matsunaga et al. 2009, Monthly Notices of the Royal
Astronomical Society, 399, 1709, através das medidas de Miras.
R0 =7,7±0,4 kpc, Andrei K. Dambis 2010, através das medidas de RR Lyrae por paralaxe estatística.
R0 =8,1±0,6 kpc, Daniel J. Majaess 2010, Acta Astronomica, 60, 55, através das medidas de RR Lyrae pelo OGLE.
R0 =7,9±0,3 kpc, Daniel J. Majaess 2009, Monthly Notices of the Royal Astronomical Society, 398, 263, através das medidas de Cefeidas.
Determinação da Velocidade do Sol
Anna-Christina Eilers, David W. Hogg, Hans-Walter Rix & Melissa Ness, no artigo The Circular Velocity Curve of the Milky Way from 5 to 25 kpc, Astrophysical Journal, Volume 871, Issue 1, article id. 120, 8 pp. (2019), encontraram
vSol=229±1 km/s (±5% sistemático), estimando uma massa em matéria escura da Via Láctea de
Mvirial=(7,25±0,2)×1011MSol.


Próxima: Populações Estelares
Volta: Nossa Galáxia: a Via Láctea
Anterior: Movimento das Estrelas
©
Modificada em 27 set 2023




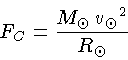
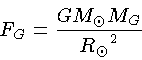
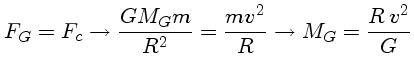
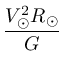 =
=
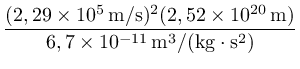

 Essa massa, que só interage pela gravidade,
ainda não foi detectada em laboratório e constitui um dos
pontos mais perplexantes da astronomia moderna. Está
distribuída em um halo extenso em torno da Galáxia. Conclusão: a curva
de rotação observada prova que existe matéria escura em nossa Galáxia
e que ela é dominante.
Essa massa, que só interage pela gravidade,
ainda não foi detectada em laboratório e constitui um dos
pontos mais perplexantes da astronomia moderna. Está
distribuída em um halo extenso em torno da Galáxia. Conclusão: a curva
de rotação observada prova que existe matéria escura em nossa Galáxia
e que ela é dominante.



![]()
![]()
![]()