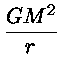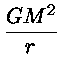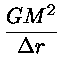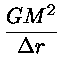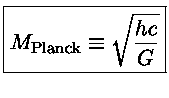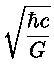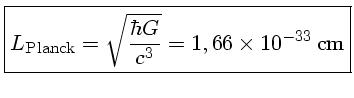Massa de Planck
A energia gravitacional é dada por:
EG 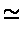
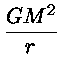
desprezando-se o fator de integração, da ordem de 3/5 para
distribuições esféricas.
Assumindo que a massa seja constante, podemos escrever em primeira ordem:
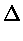 E
E =
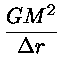
O princípio da incerteza pode ser escrito como
Note que usamos h e não 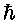 porque estamos usando r e p
em módulo, e não somente em uma direção.
Mas
porque estamos usando r e p
em módulo, e não somente em uma direção.
Mas
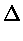 E
E =
c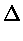 p
p
Logo
e podemos escrever:
GM2 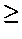 hc
hc
Definimos a massa de Planck como:
Nosso valor difere do valor na literatura
MPlanck=
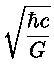
devido ao uso de h e não 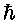 na equação
1
na equação
1
O comprimento de Planck é dado por:
Volta:
Cosmologia Matemática
Volta: Astronomia e Astrofísica
©
Modificada em 12 Dez 2004