Aberrações são desvios de um sistema ótico das previsões da ótica
paraxial
(válida para ângulos pequenos em relação ao eixo de referência do sistema)
[Johann Carl Friedrich Gauss (1777-1855), Dioptrische Untersuchungen, Göttingen, 1841]
produzindo borramento da imagem, já que cada ponto do objeto não
converge para um único ponto da imagem. As aberrações se dividem
em monocromáticas, ou geométricas, e cromáticas, causadas por
dispersão, isto é, pela variação do índice de refração com o
comprimento de onda.
A ótica ativa
consiste no ajuste do espelho primário em baixa freqüência,
de escalas de tempo da ordem de segundos, para corrigir distorções
causadas pela ação da gravidade e gradientes de temperaturas.
 A
ótica adaptativa
consiste no
ajuste do secundário ou terciário (deformáveis, corretores de fase)
em alta freqüência,
de 50 Hz a 10 mil Hz,
para compensar em tempo real as deformações introduzidas
no feixe pela atmosfera da Terra.
Os espelhos deformáveis têm centenas de pequenos pistões (atuadores),
acionados eletrônicamente, que ajustam a altura da superfície
refletora por alguns mícrons em alguns microsegundos,
retardando ou adiantando da radiação naquele ponto.
A
ótica adaptativa
consiste no
ajuste do secundário ou terciário (deformáveis, corretores de fase)
em alta freqüência,
de 50 Hz a 10 mil Hz,
para compensar em tempo real as deformações introduzidas
no feixe pela atmosfera da Terra.
Os espelhos deformáveis têm centenas de pequenos pistões (atuadores),
acionados eletrônicamente, que ajustam a altura da superfície
refletora por alguns mícrons em alguns microsegundos,
retardando ou adiantando da radiação naquele ponto.
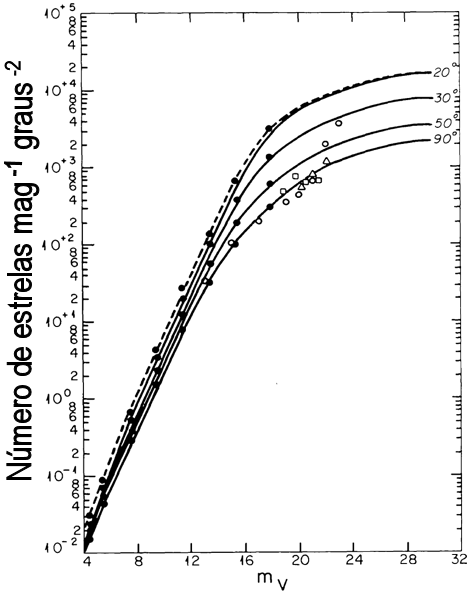 Uma estrela de magnitude visual
V = 0 tem um fluxo observado de
Uma estrela de magnitude visual
V = 0 tem um fluxo observado de
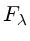 =3,69 ×109 erg cm-2 s-1 Å-1
que corresponde a
cerca de 1000 fótons cm-2 s-1 Å-1.
Para ótica adaptativa, precisamos detectar fótons em vários píxeis
do detector de frente de onda a cada exposição de milésimos de segundos,
mas existem poucas estrelas tão brilhantes no céu, principalmente
dentro do campo de alguns minutos de arco de um telescópio de grande porte
[John Norris Bahcall (1934-2005) & Raymond M. Soneira (1980) Astrophysical
Journal Supplement Series, 44, 73]
Nos telescópios de 8 a 10 m atuais, somente estrelas mais brilhantes que R=15 podem ser usadas como
estrelas de referência e somente cerca de 5% do céu tem estrelas tão brilhantes próximas.
=3,69 ×109 erg cm-2 s-1 Å-1
que corresponde a
cerca de 1000 fótons cm-2 s-1 Å-1.
Para ótica adaptativa, precisamos detectar fótons em vários píxeis
do detector de frente de onda a cada exposição de milésimos de segundos,
mas existem poucas estrelas tão brilhantes no céu, principalmente
dentro do campo de alguns minutos de arco de um telescópio de grande porte
[John Norris Bahcall (1934-2005) & Raymond M. Soneira (1980) Astrophysical
Journal Supplement Series, 44, 73]
Nos telescópios de 8 a 10 m atuais, somente estrelas mais brilhantes que R=15 podem ser usadas como
estrelas de referência e somente cerca de 5% do céu tem estrelas tão brilhantes próximas.
Por isto faz-se necessário criar estrelas artificais com lasers, que
atingem uma altura de 90 a 100 quilômetros, na mesosfera, for fluorescência de
átomos de sódio,
não podendo corrigir
os efeitos da alta atmosfera.
Como a fonte é observada superposta à luz espalhada de fontes
terrestres, da luz das estrelas e da Lua, emissão difusa
da Galáxia, luz zodiacal, etc, podemos aumentar a
razão sinal-ruído da fonte simplesmente diminuindo
o tamanho da imagem, pois isto diminui a quantidade de
píxeis com ruído que precisam ser somados para medir a fonte.
Função de Espalhamento Puntual (Point Spread Function)
A imagem produzida por um telescópio em geral não é ideal, isto é, não
segue um disco de difração (de Airy), devido à turbulência atmosférica,
degradando a resolução. A refração pelas células
da atmosfera é maior do que o limite de difração, em geral.
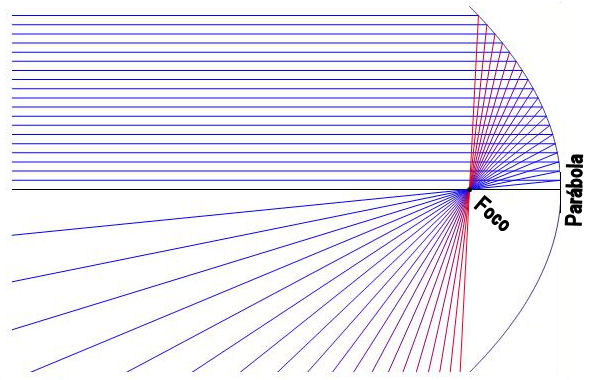
O disco de Airy é definido como o disco até o primeiro
mínimo do padrão de interferência por difração.
A Função de Espalhamento Puntual
(Point Spread Function, PSF)
é a função que descreve a distribuição de luz produzida por uma
imagem puntual, no plano da imagem,
e sua largura mede a resolução real da imagem.
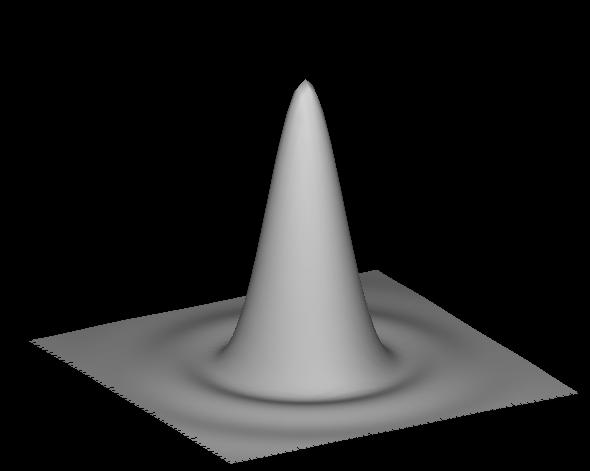
No limite de difração,
onde P(r) é a intensidade no ponto r,
J1 é a função de Bessel de primeira ordem,
J1(x)=x/2-x3/(231!2!)+x5/(252!3!)+...,
λ o comprimento
de onda e D o diâmetro do telescópio.
Desta forma, P(r) é zero ou atinge um máximo de acordo com os zeros
e máximos da função de Bessel J1. Os primeiros
zeros ocorrem para θ=1,220λ/D, 2,233λ/D e 3,238λ/D.
Quando o centro do disco de Airy de uma fonte se sobrepõe ao primeiro
mínimo de outra fonte, obtemos o critério de Rayleigh para a
resolução.
A atmosfera preserva o fluxo total do objeto, mas distribui a energia diferentemente entre os píxeis. Se a PSF
[P(r)] tem a mesma forma sobre todo o campo
da imagem, chamamos esta condição de isoplanática.
Isto não ocorre em geral, principalmente com a aplicação da ótica
adaptativa, e a equação da imagem só é aplicável a parte da imagem.
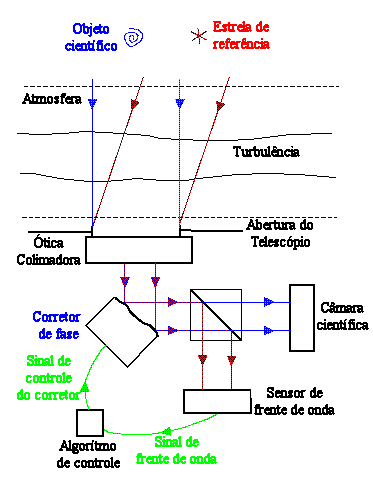
As aberrações são medidas pelo sensor de frente de onda, em tempo real,
que mede a estrela de referência, que pode ser uma estrela natural
ou uma estrela artificial criada na alta atmosfera por um laser.
Para o Altair, no Gemini, o campo corrigido é da ordem de 7" (50%), enquanto para o MCAO, 1'.
 O algorítmo de controle usa a aberração medida em tempo real para
calcular as deformações que produziriam uma imagem sem qualquer aberração.
A luz do objeto científico também é corrigida pelo espelho
deformável, mas direcionada para a câmara científica.
O algorítmo de controle usa a aberração medida em tempo real para
calcular as deformações que produziriam uma imagem sem qualquer aberração.
A luz do objeto científico também é corrigida pelo espelho
deformável, mas direcionada para a câmara científica.
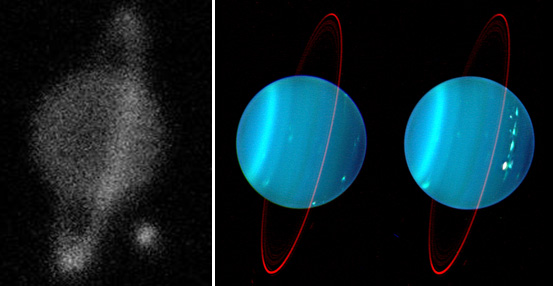 Imagem de Urano no Observatório Keck, com telescópio de 10 m de diâmetro, de Urano, sem ótica adaptativa (esquerda) e com
ótica adaptiva (direita).
Imagem de Urano no Observatório Keck, com telescópio de 10 m de diâmetro, de Urano, sem ótica adaptativa (esquerda) e com
ótica adaptiva (direita).
A correção adaptativa de mais baixa ordem corresponde a
inclinar e mover (tip-tilt), corrigindo as inclinações da frente de onda em
duas dimensões (deslocamento de posição e ângulo). Esta correção
é feita movendo rapidamente o espelho de tip-tilt que faz
pequenas rotações em seus dois eixos. Estes movimentos corrigem
significativamente as aberrações introduzidas pela atmosfera.
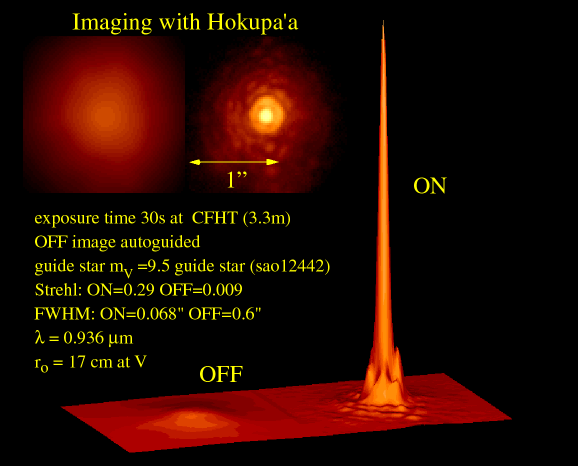
Ótica ativa no CFHT.
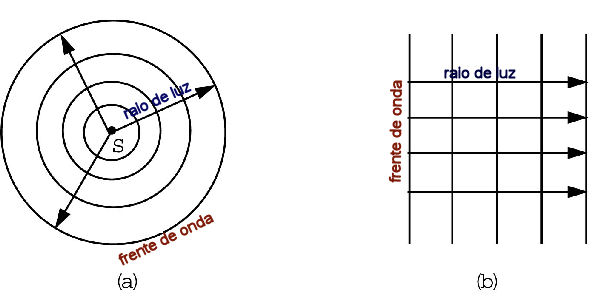
Refração
A refração da luz foi estudada
em 1621 pelo matemático e físico holandês
Willebrord Snell (1591-1626) e descrita pelo filósofo francês René Descartes
(1596-1650) no seu livro Dioptrics de 1637.
Se um feixe em um meio de índice de refração n incide com
um ângulo i em uma superfície de um meio de índice de refração
n′, o feixe emergente neste meio terá um ângulo i′
dado pela lei de refração de Snell-Descartes:
n sen(i)=n′ sen(i′)
Qualquer superfície z pode ser descrita numa expansão polinomial:
z = ao+ a1y+ a2y2+ a3y3+ a4y4+ ...
Se definirmos a superfície como centrada em z=0:
z = a1y+ a2y2+ a3y3+ a4y4+ ...
e se a superfície for simétrica em relação ao eixo z=0,
somente os termos pares (simétricos) serão não nulos:
z = a2y2+ a4y4+ a6y6+ ...
A ótica gaussiana (paraxial) é por definição parabólica, de modo que o termo
z = a2y2 define uma ótica gaussiana.
Podemos também expandir os senos em séries de Taylor:
sen(i) = i - i3/3!- i5/5! - ...
e definir a expansão em primeira ordem da Lei de Snell-Descartes como:
n i = n′i′
que é a forma paraxial (ângulos pequenos) da lei.
Qualquer desvio da aproximação de Gauss é chamada de aberração.
 Quando a luz
de comprimento de onda λ
passa por uma abertura, como o espelho primário de um
telescópio de diâmetro D, ela sofre difração e
os máximos da luz difratada ocorrem para ângulos
θmáximo tais que:
Quando a luz
de comprimento de onda λ
passa por uma abertura, como o espelho primário de um
telescópio de diâmetro D, ela sofre difração e
os máximos da luz difratada ocorrem para ângulos
θmáximo tais que:
D sen(θmáximo)=|n|λ, n=0,1,2,3,...
como encontrado
empiricamente por Thomas Young (1773-1809), em 1801,
e
Joseph von Fraunhofer (1787-1826).
Se a luz incide com um ângulo i, a relação se torna
D[sen(θmáximo)+sen(i)]=|n|λ, n=0,1,2,3,...
que é chamada equação de rede de difração de Fraunhofer.
A
razão Strehl é a razão entre a intensidade máxima
observada no plano do telescópio
de uma fonte puntual, comparada com a intensidade teórica máxima de um
sistema perfeito no limite de difração, S=P(0)/PA(0), definido por
Karl Strehl (1864-1940)
[1895,
Aplanatische und fehlerhafte Abbildung im Fernrohr,
Zeitschrift für Instrumentenkunde, 15 (Oct.), 362-370 e
1902,
Über Luftschlieren und Zonenfehler,
Zeitschrift für Instrumentenkunde, 22 (July), 213-217].
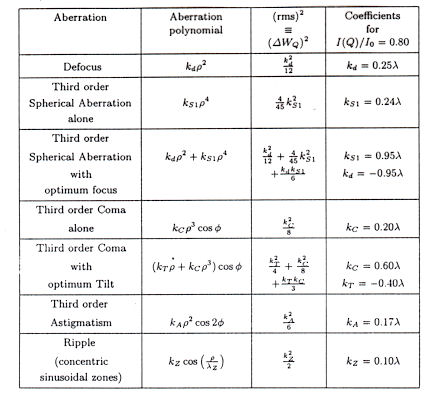
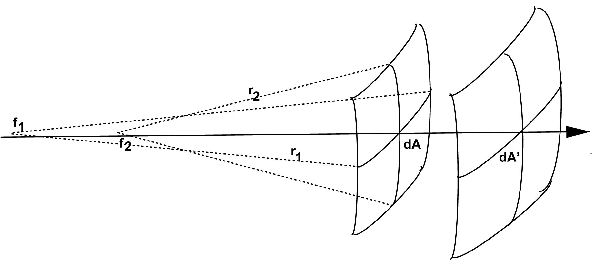
Na tabela são listadas as aberrações
que resultam em uma razão de intensidades Strehl de 80%, para uma
fonte puntual, não coerente e sem vinhetamento.
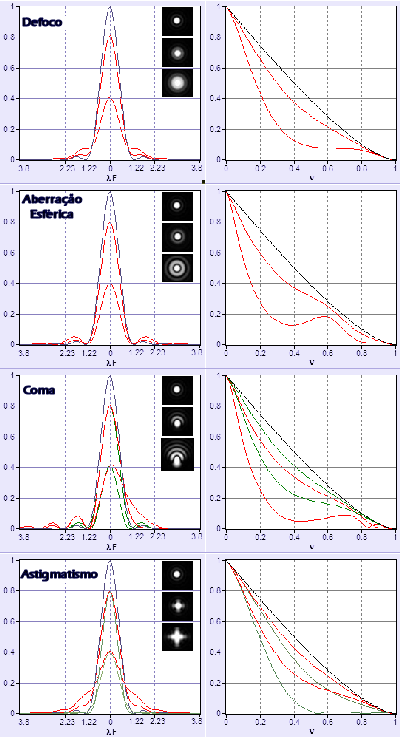
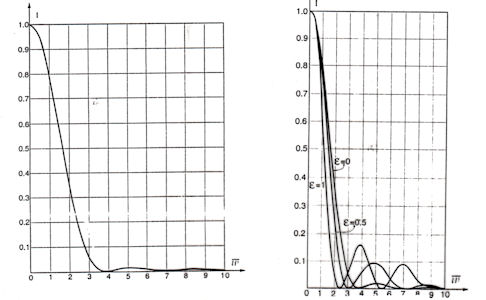
Redução na razão Strehl por aberração.
A imagem e linha (PSF = point spread function, função
de espalhamento de imagem à esquerda) mais alta correspondem a imagem sem aberração, a seguinte com
Strehl de 0,8 e a mais baixa com o dobro desta aberração, Strehl de 0,4.
O gráfico à direita mostra o contraste (área comum normalizada de dois círculos separados por ν),
de
Telescope Optics.
A turbulência atmosférica faz com a onda plana incidente seja deformada. A parte da onda que atinge um parte da atmosfera mais quente e, portanto, com índice de refração menor,
é adiantada em relação à outra.
Como a turbulência atmosférica varia de célula para célula (raio de coerência de Fried),
as perturbações de fase diferem de uma célula para outra, e a compensação
calculada na direção de estrela de referência se degrada em outras direções.
Para a ótica adaptativa utilizada atualmente nos telescópios no Chile e
em Mauna Kea, o ângulo isoplanático, definido como o ângulo a partir da
estrela de referência em que a razão de Strehl cai por 50%, é da
ordem de 20" em J (1,2 μm), a 40" em K (2,2 μm).


Laser multiconjudado no Gemini sul e imagem da nebulosa de Órion obtida com o GEMS (sistema de ótica ativa multiconjudaga) do telescópio Gemini sul.
O Gemini Sul lançou em 2011 um laser de 589 nm gerando pela primeira vez 5 estrelas
a 90 km de altura, excitando íons de sódio (Gemini
Multiconjugate Adaptative Optics), com o objetivo de atingir um campo isoplanático de um alguns minutos de arco,
já que diferentes sensores de onda permitirão uma correção integrada, utilizando-se mais
de um espelhos deformáveis.
Note um ganho de um fator de 2× na PSF (seeing) significa
um fator de 4× na concentração da luz captada de uma fonte puntual,
ou 0,75 magnitude no ganho.
Note também que galáxias com z>1 podem ser consideradas como puntuais,
já que têm cerca
de 0,2", independente de z.
Em 1934, o físico holandês
Frits Zernike
(1888-1966),
ganhador do prêmio Nobel de 1953 por sua invenção
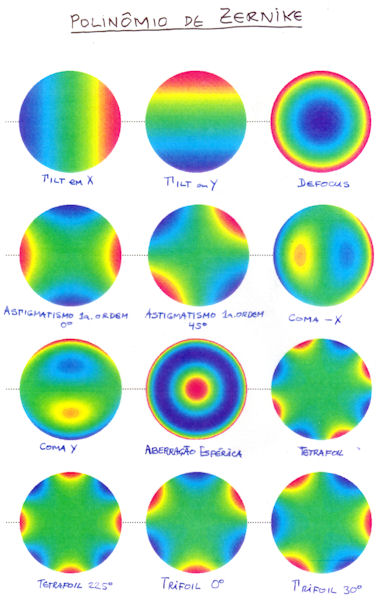
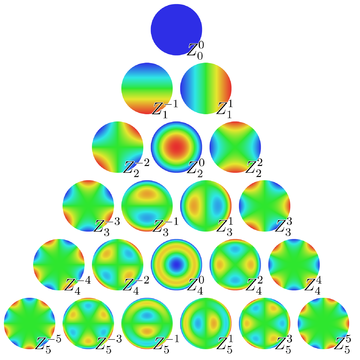
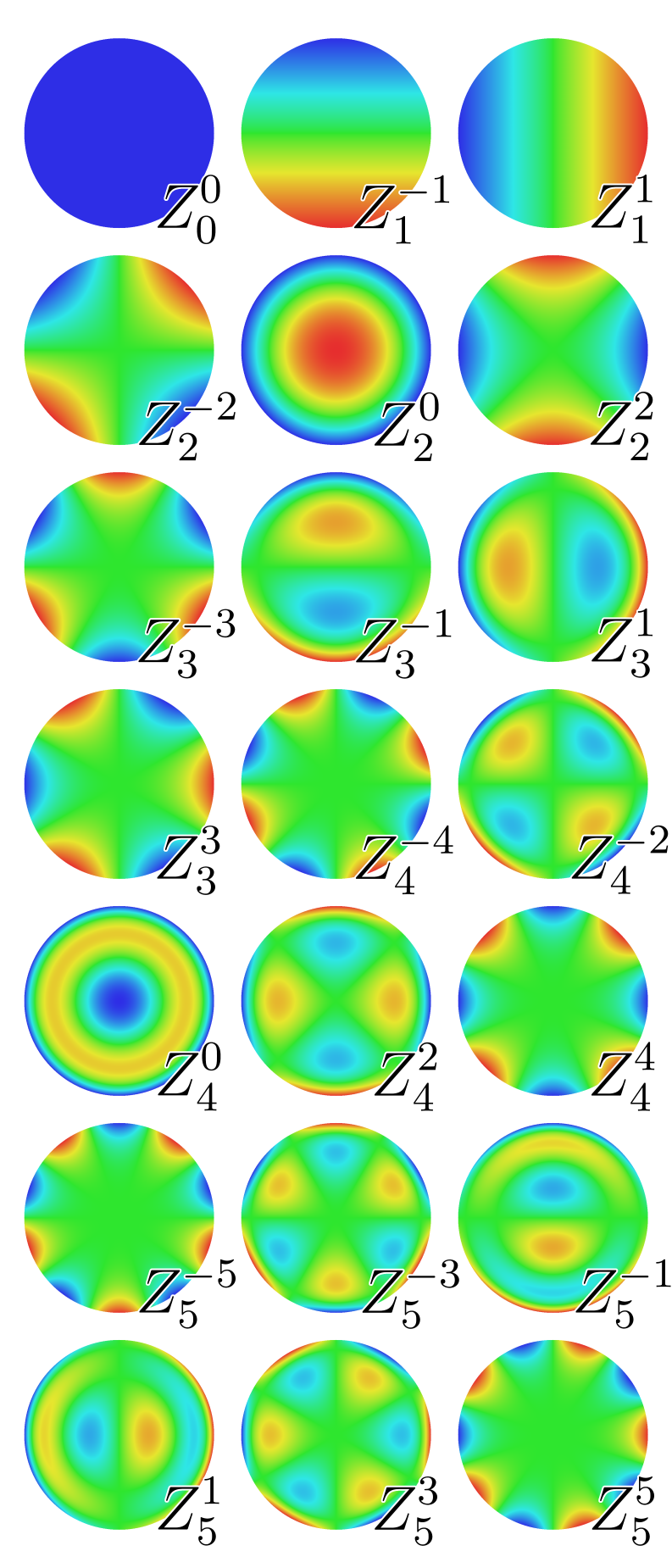
do microscópio de contraste de fase, propôs a decomposição
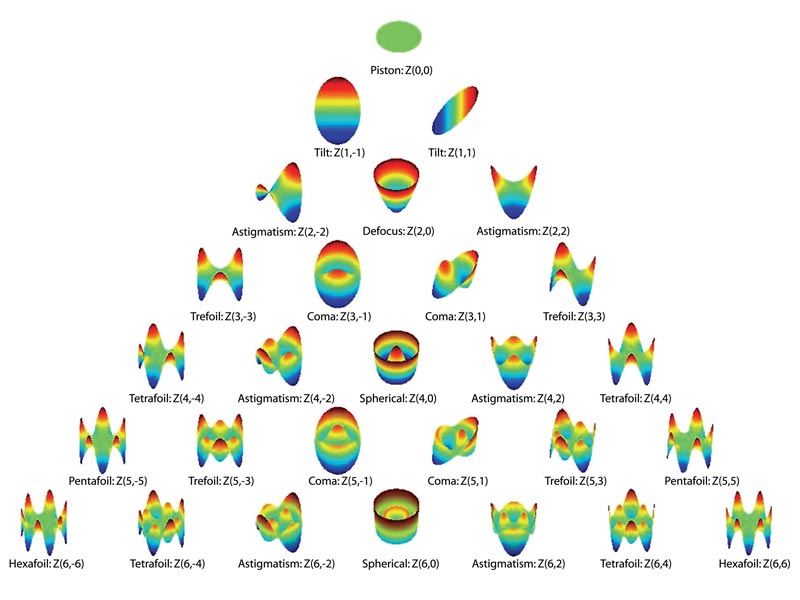
em polinômios de Zernike, um conjunto
ortogonal que permite a separação clara
dos diversos efeitos de aberração.
Os polinômios pares são dados por
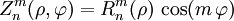
os ímpares por
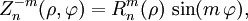
com a parte radial dada por
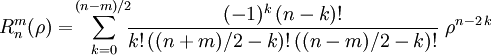 se n-m é par, e
se n-m é par, e
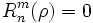 se n-m é impar,
onde m e n são inteiros não negativos, com m>n, φ
o ângulo azimutal em radianos, e ρ a coordenada radial normalizada.
se n-m é impar,
onde m e n são inteiros não negativos, com m>n, φ
o ângulo azimutal em radianos, e ρ a coordenada radial normalizada.
Tutorial
sobre ótica adaptativa de Andrei Tokovin, do CTIO
 SAM (SOAR Adaptive Module) - Módulo de ótica adaptativa do Soar, desenvolvido por Andrei Tokovin. Imagem
do sistema triplo I385 (HIP 85216) com duas componentes a 0,39 e 0,26
segundos de arco, obtida em 2 de outubro de 2009, na banda I. A resolução
é da ordem de 0,1 segundos de arco.
SAM (SOAR Adaptive Module) - Módulo de ótica adaptativa do Soar, desenvolvido por Andrei Tokovin. Imagem
do sistema triplo I385 (HIP 85216) com duas componentes a 0,39 e 0,26
segundos de arco, obtida em 2 de outubro de 2009, na banda I. A resolução
é da ordem de 0,1 segundos de arco.
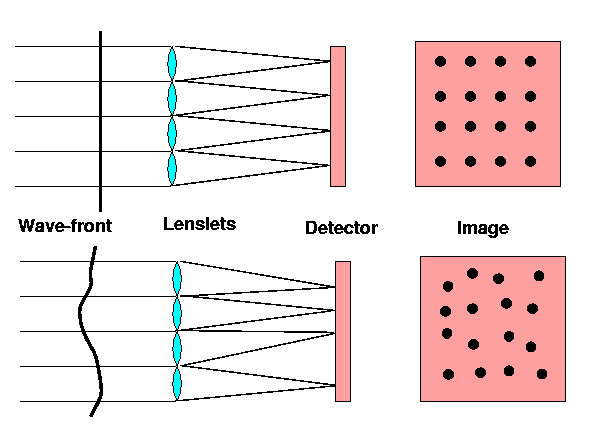 Um sensor de frente de onda para astronomia precisa ser eficiente, trabalhar com luz branca e ser rápido, pois as fontes são fracas.
Um sensor de frente de onda muito utilizado é conhecido como Shack-Hartmann
(Johannes Franz Hartmann (1865-1936), 1900,
Bemerkungen über den Bau und die Justirung von Spektrographen. Zeitung Instrumentenkd, 20, 47;
Roland V. Shack & Ben C. Platt, 1971, Production and use of a lenticular Hartmann screen,
Journal of the Optical Society of America, 61, 656) e utiliza um conjunto
de pequenas lentes para projetar uma imagem
em um CCD e permitir a medida dos deslocamentos da frente da onda.
Se a frente de onda não for plana, as imagens são deslocadas de sua posição regular.
Um sensor de frente de onda para astronomia precisa ser eficiente, trabalhar com luz branca e ser rápido, pois as fontes são fracas.
Um sensor de frente de onda muito utilizado é conhecido como Shack-Hartmann
(Johannes Franz Hartmann (1865-1936), 1900,
Bemerkungen über den Bau und die Justirung von Spektrographen. Zeitung Instrumentenkd, 20, 47;
Roland V. Shack & Ben C. Platt, 1971, Production and use of a lenticular Hartmann screen,
Journal of the Optical Society of America, 61, 656) e utiliza um conjunto
de pequenas lentes para projetar uma imagem
em um CCD e permitir a medida dos deslocamentos da frente da onda.
Se a frente de onda não for plana, as imagens são deslocadas de sua posição regular.
Matematicamente, a imagem observada é a convolução da imagem original,
Io,
com a função que descreve a distorção atmosférica (Φ):
I(x,y) = ∑i,j Io (i,j) Φ(x+i,y+j)
Em 1941,
Andrei Nikolaevich Kolmogorov (1903-1987)
(Doklady Akademii Nauk S.S.S.R, 30, 229) propôs que
em um meio turbulento, a energia cinética dos movimentos
de larga escala é transferida para movimentos com escalas
cada vez menores, até que este processo pare quando
a energia cinética for dissipada por fricção viscosa.
Num estado estacionário, a dissipação de energia
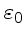 deve ser igual à taxa de produção de
energia turbulenta.
Seguindo este raciocínio, Kolmogorov
assumiu que a velocidade
deve ser igual à taxa de produção de
energia turbulenta.
Seguindo este raciocínio, Kolmogorov
assumiu que a velocidade 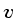 do movimento é proporcional
à escala
do movimento é proporcional
à escala 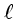 e à taxa de produção e
dissipação de energia
e à taxa de produção e
dissipação de energia
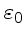 .
Como nas escalas maiores
.
Como nas escalas maiores
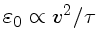 ,
onde
,
onde 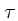 é o tempo característico
é o tempo característico
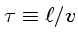 ,
Em uma análise espectral (de Fourier) da energia cinética em função
de um número de onda
,
Em uma análise espectral (de Fourier) da energia cinética em função
de um número de onda
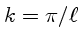 ,
a energia
,
a energia 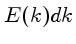 entre
entre
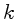 e
e 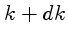 é proporcional a
é proporcional a 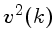 , logo
conhecida como a lei de Kolmogorov, que só é valida longe das bordas
, logo
conhecida como a lei de Kolmogorov, que só é valida longe das bordas
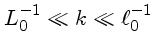 , onde
, onde 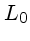 é a escala externa,
geralmente a escala da região que dá origem à turbulência,
e
é a escala externa,
geralmente a escala da região que dá origem à turbulência,
e  a escala na qual a dissipação por viscosidade ocorre.
Neste modelo, a intensidade no ponto r
é dada por P(r)=exp[-3.44(λr/r0)5/3], onde r0 é a escala de coerência atmosférica, o parâmetro de Fried,
representando a escala característica da atmosfera.
Este modelo é
a base da Ótica Adaptativa,
e resulta em uma imagem com
a escala na qual a dissipação por viscosidade ocorre.
Neste modelo, a intensidade no ponto r
é dada por P(r)=exp[-3.44(λr/r0)5/3], onde r0 é a escala de coerência atmosférica, o parâmetro de Fried,
representando a escala característica da atmosfera.
Este modelo é
a base da Ótica Adaptativa,
e resulta em uma imagem com
Point Spread Function=seeing=0.98λ/r0
Para λ=5000 Å e r0=10 cm → PSF=1".
Para um ótimo sítio, r0=30 cm, e PSF=0.3".
A razão Strehl para a PSF atmosférica é igual a um telescópio ideal de diâmetro r0.
Gráfico dos polinômios, de Lakshminarayanan V., Fleck A., Zernike polynomials: a guide, Journal of Modern Optics, 2011, vol. 58, p. 545.
Tutorial de
Andrei A. Tokovinin (CTIO) sobre ótica adaptativa
Páginas do Gemini sobre ótica adaptativa.
O Natural Guide System precisa de estrelas mais brilhantes que m=13, e o laser no GN tem 10W. MCAO laser 31W.
Página, em inglês, sobre aberrações óticas.
Página sobre ótica adaptativa multiconjugada do Gemini
Ótica Adpativa no ESO. Estão desenvolvendo o 4LGSF, com 4 lasers de 20 W.


Próxima: Detectores
Volta: Astrometria
Anterior: Telescópios
©
Modificada em 30 nov 2018

 A
ótica adaptativa
consiste no
ajuste do secundário ou terciário (deformáveis, corretores de fase)
em alta freqüência,
de 50 Hz a 10 mil Hz,
para compensar em tempo real as deformações introduzidas
no feixe pela atmosfera da Terra.
Os espelhos deformáveis têm centenas de pequenos pistões (atuadores),
acionados eletrônicamente, que ajustam a altura da superfície
refletora por alguns mícrons em alguns microsegundos,
retardando ou adiantando da radiação naquele ponto.
A
ótica adaptativa
consiste no
ajuste do secundário ou terciário (deformáveis, corretores de fase)
em alta freqüência,
de 50 Hz a 10 mil Hz,
para compensar em tempo real as deformações introduzidas
no feixe pela atmosfera da Terra.
Os espelhos deformáveis têm centenas de pequenos pistões (atuadores),
acionados eletrônicamente, que ajustam a altura da superfície
refletora por alguns mícrons em alguns microsegundos,
retardando ou adiantando da radiação naquele ponto.
 Uma estrela de magnitude visual
V = 0 tem um fluxo observado de
Uma estrela de magnitude visual
V = 0 tem um fluxo observado de
![]() =3,69 ×109 erg cm-2 s-1 Å-1
que corresponde a
cerca de 1000 fótons cm-2 s-1 Å-1.
Para ótica adaptativa, precisamos detectar fótons em vários píxeis
do detector de frente de onda a cada exposição de milésimos de segundos,
mas existem poucas estrelas tão brilhantes no céu, principalmente
dentro do campo de alguns minutos de arco de um telescópio de grande porte
[John Norris Bahcall (1934-2005) & Raymond M. Soneira (1980) Astrophysical
Journal Supplement Series, 44, 73]
Nos telescópios de 8 a 10 m atuais, somente estrelas mais brilhantes que R=15 podem ser usadas como
estrelas de referência e somente cerca de 5% do céu tem estrelas tão brilhantes próximas.
=3,69 ×109 erg cm-2 s-1 Å-1
que corresponde a
cerca de 1000 fótons cm-2 s-1 Å-1.
Para ótica adaptativa, precisamos detectar fótons em vários píxeis
do detector de frente de onda a cada exposição de milésimos de segundos,
mas existem poucas estrelas tão brilhantes no céu, principalmente
dentro do campo de alguns minutos de arco de um telescópio de grande porte
[John Norris Bahcall (1934-2005) & Raymond M. Soneira (1980) Astrophysical
Journal Supplement Series, 44, 73]
Nos telescópios de 8 a 10 m atuais, somente estrelas mais brilhantes que R=15 podem ser usadas como
estrelas de referência e somente cerca de 5% do céu tem estrelas tão brilhantes próximas.

![$P(\vec{r}) = \frac{\pi D^2}{4 \lambda^2}
[\frac{2J_1(\pi D\vert\vec{r}\vert/\lambda)}{\pi D\vert\vec{r}\vert/\lambda)}]^2
\eqno{1}$](psf.png)
 O algorítmo de controle usa a aberração medida em tempo real para
calcular as deformações que produziriam uma imagem sem qualquer aberração.
A luz do objeto científico também é corrigida pelo espelho
deformável, mas direcionada para a câmara científica.
O algorítmo de controle usa a aberração medida em tempo real para
calcular as deformações que produziriam uma imagem sem qualquer aberração.
A luz do objeto científico também é corrigida pelo espelho
deformável, mas direcionada para a câmara científica.
 Imagem de Urano no Observatório Keck, com telescópio de 10 m de diâmetro, de Urano, sem ótica adaptativa (esquerda) e com
ótica adaptiva (direita).
Imagem de Urano no Observatório Keck, com telescópio de 10 m de diâmetro, de Urano, sem ótica adaptativa (esquerda) e com
ótica adaptiva (direita).


 Quando a luz
de comprimento de onda λ
passa por uma abertura, como o espelho primário de um
telescópio de diâmetro D, ela sofre difração e
os máximos da luz difratada ocorrem para ângulos
θmáximo tais que:
Quando a luz
de comprimento de onda λ
passa por uma abertura, como o espelho primário de um
telescópio de diâmetro D, ela sofre difração e
os máximos da luz difratada ocorrem para ângulos
θmáximo tais que:





![]()
![]()
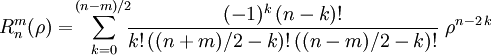 se n-m é par, e
se n-m é par, e
![]() se n-m é impar,
onde m e n são inteiros não negativos, com m>n, φ
o ângulo azimutal em radianos, e ρ a coordenada radial normalizada.
se n-m é impar,
onde m e n são inteiros não negativos, com m>n, φ
o ângulo azimutal em radianos, e ρ a coordenada radial normalizada.



 SAM (SOAR Adaptive Module) - Módulo de ótica adaptativa do Soar, desenvolvido por Andrei Tokovin. Imagem
do sistema triplo I385 (HIP 85216) com duas componentes a 0,39 e 0,26
segundos de arco, obtida em 2 de outubro de 2009, na banda I. A resolução
é da ordem de 0,1 segundos de arco.
SAM (SOAR Adaptive Module) - Módulo de ótica adaptativa do Soar, desenvolvido por Andrei Tokovin. Imagem
do sistema triplo I385 (HIP 85216) com duas componentes a 0,39 e 0,26
segundos de arco, obtida em 2 de outubro de 2009, na banda I. A resolução
é da ordem de 0,1 segundos de arco.
 Um sensor de frente de onda para astronomia precisa ser eficiente, trabalhar com luz branca e ser rápido, pois as fontes são fracas.
Um sensor de frente de onda muito utilizado é conhecido como Shack-Hartmann
(Johannes Franz Hartmann (1865-1936), 1900,
Bemerkungen über den Bau und die Justirung von Spektrographen. Zeitung Instrumentenkd, 20, 47;
Roland V. Shack & Ben C. Platt, 1971, Production and use of a lenticular Hartmann screen,
Journal of the Optical Society of America, 61, 656) e utiliza um conjunto
de pequenas lentes para projetar uma imagem
em um CCD e permitir a medida dos deslocamentos da frente da onda.
Se a frente de onda não for plana, as imagens são deslocadas de sua posição regular.
Um sensor de frente de onda para astronomia precisa ser eficiente, trabalhar com luz branca e ser rápido, pois as fontes são fracas.
Um sensor de frente de onda muito utilizado é conhecido como Shack-Hartmann
(Johannes Franz Hartmann (1865-1936), 1900,
Bemerkungen über den Bau und die Justirung von Spektrographen. Zeitung Instrumentenkd, 20, 47;
Roland V. Shack & Ben C. Platt, 1971, Production and use of a lenticular Hartmann screen,
Journal of the Optical Society of America, 61, 656) e utiliza um conjunto
de pequenas lentes para projetar uma imagem
em um CCD e permitir a medida dos deslocamentos da frente da onda.
Se a frente de onda não for plana, as imagens são deslocadas de sua posição regular.
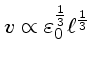
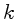 e
e 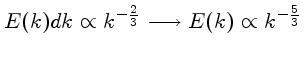
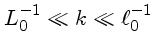 , onde
, onde