Conjunto Completo de Funções

Duas funções são ortogonais se o produto interno entre elas é nulo:

$$\int_{x_1}^{x_2} f(x)g(x)dx = 0$$

e são normalizadas se o produto da função consigo mesmo for igual a 1:

$$\int_{x_1}^{x_2} f(x)f(x)dx = 1$$

Um conjunto de funções $\{h_i(x)\}$ é ortonormal se suas funções forem ortogonais e normalizadas:

$$\int_{x_1}^{x_2} h_i(x)h_j(x)dx = \delta_{ij}$$

onde $\delta_{ij}$ é o delta de Kronecker. O produto interno de duas funções complexas é definido como:

$$\int_{x_1}^{x_2} f(x)^*g(x)dx$$

onde $f(x)^*$ é o complexo conjugado de $f(x)$, de modo que a relação de ortonormalidade para um conjunto de funções complexas é:

$$\int_{x_1}^{x_2} h_i^*(x)h_j(x)dx = \delta_{ij}$$

Um conjunto de funções $\{h_i(x)\}$ é chamado de completo se, para qualquer função bem comportada $f(x)$, existir um comjunto de números $a_i$,

$$f(x)=\sum_i a_i h_i(x)$$

tal que

$$\int_{x_1}^{x_2} \Big(f(x)-\sum_i a_i h_i(x)\Big)^2 dx = 0$$

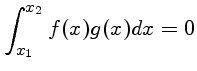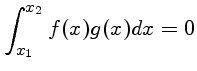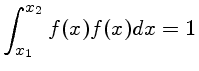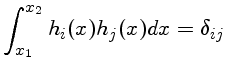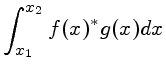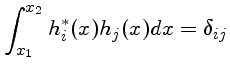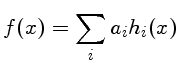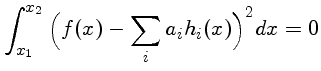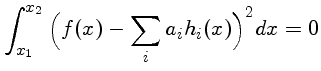
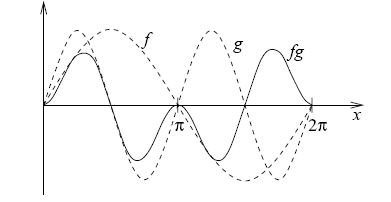
O conjunto de funções senos é ortonormal. No gráfico temos f=sen x e g=sen 2x. A integral sobre um ciclo é nula.

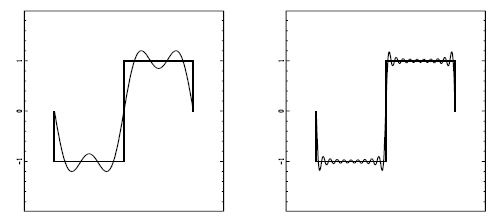
À esquerda mostramos a soma dos dois primeiros termos da série de Fourier fitada a uma função degrau. À direita, a soma dos 10 primeiro termos.

Volta: Transformadas de Fourier