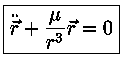 (1)
(1)
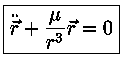 (1)
(1)
Multiplicando-se vetorialmente a equação (1) por ![]() :
:
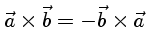 .
A parte da direita de (4) pode ser escrita como:
.
A parte da direita de (4) pode ser escrita como:
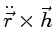 ,
pode ser escrito como:
,
pode ser escrito como:
Juntando os dois lados, a equação (4) pode então ser escrita como:
Até agora encontramos dois vetores constantes,
![]() e
e ![]() , e
um escalar constante,
ε, de modo que já
temos 7 integrais.
Entretanto, elas não são todas independentes. Por exemplo, como
, e
um escalar constante,
ε, de modo que já
temos 7 integrais.
Entretanto, elas não são todas independentes. Por exemplo, como ![]() está no plano da órbita, e
está no plano da órbita, e ![]() em um plano perpendicular a este,
em um plano perpendicular a este, ![]() ·
·![]() =0.
=0.
Multiplicando-se (4a) escalarmente por ![]() ,
temos:
,
temos:
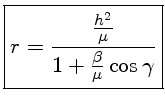
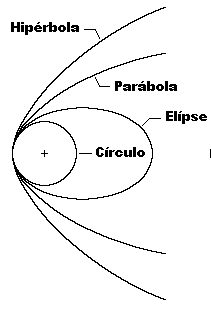
Esta é a equação de uma cônica (círculo, elipse, parábola ou hipérbole) com foco na origem, em coordenadas polares. As cônicas foram estudadas pelo matemático grego Apolônio de Perga (c. 262 a.C.- c. 190 a.C.) em 200 a.C.
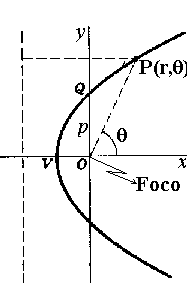
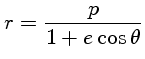
 Somente para β/μ<1 o movimento é finito, e
a órbita é uma elipse, ou um círculo (e=0).
Somente para β/μ<1 o movimento é finito, e
a órbita é uma elipse, ou um círculo (e=0).
Note que ![]() é mínimo quando γ=0 (θ=0 na equação da cônica),
isto é, na direção de
é mínimo quando γ=0 (θ=0 na equação da cônica),
isto é, na direção de ![]() ,
provando que
,
provando que ![]() aponta na direção do pericentro.
aponta na direção do pericentro.
Lembrando que μ = G(m + M), e comparando com a equação da elipse (ver Apêndice),
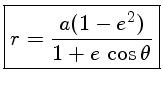
Se a excentricidade e = β/μ ≥ 1, o movimento é infinito, isto é, não se repete. Se e = 1 o corpo se move em uma parábola, e se e > 1 em uma hipérbole, o que não é o caso dos planetas, mas às vezes dos cometas e asteróides.
Vamos determinar a excentricidade e. Da equação
(4a)
que introduziu
![]() temos:
temos:
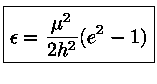
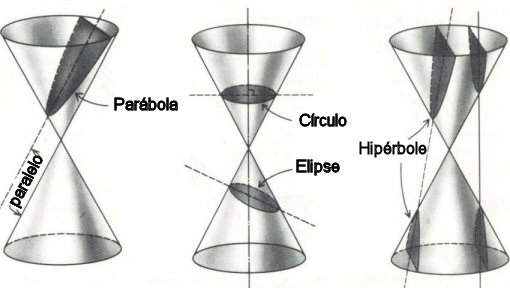
Resumindo, a lei das órbitas elípticas dos planetas é uma consequência do tipo de força que atua entre os planetas e o Sol. Newton mostrou que as únicas órbitas possíveis para um corpo interagindo gravitacionalmente com outro são as secções cônicas: círculo, elipse, parábola ou hipérbole, nomes dados por Apolônio de Perga.
Um círculo pode ser pensado como uma elipse com e = 0 e a = b. Uma parábola pode ser pensada como uma elipse com e = 1 e a = ∞. Uma hipérbole pode ser pensada como uma elipse com e > 1 e a < 0.
Se o corpo tiver movimento periódico, como os planetas, sua trajetória será circular ou elíptica; se o movimento for não periódico, como é o caso de alguns cometas e asteróides, a trajetória será parabólica ou hiperbólica. O fator decisivo sobre o tipo de órbita é a energia do sistema, detalhado adiante. A órbita circular é a de menor energia possível, mas requer que as condições iniciais do movimento sejam perfeitas, o que dificilmente acontece na natureza.
O termo apside refere-se à menor ou maior distância do objeto ao foco.
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)