Coordenadas Equatoriais

Dia

Movimento Diurno

Passagem Meridiana

Sistemas de Coordenadas

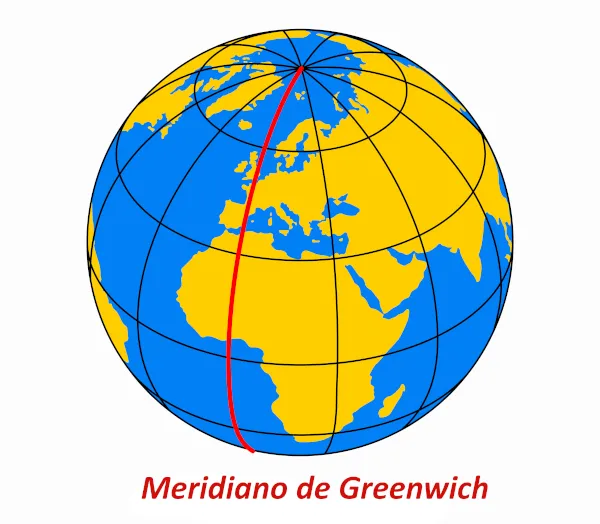
Para determinar a posição de um astro no céu, precisamos definir um sistema de coordenadas. Nesse sistema, vamos utilizar apenas coordenadas angulares, sem nos preocuparmos com as distâncias dos astros. A posição do astro será determinada através de dois ângulos de posição, um medido sobre um plano fundamental, e o outro medido perpendicularmente a ele. Antes de entrarmos nos sistemas de coordenadas astronômicas, convém recordarmos o sistema de coordenadas geográficas, usadas para medir posição sobre a superfície da Terra. Nesse sistema as coordenadas são latitude e a longitude.

• longitude geográfica (λ): é o ângulo medido ao longo do equador da Terra, tendo origem em um meridiano de referência (o meridiano de Greenwich), e extremidade no meridiano do lugar. Na Conferência Internacional Meridiana, realizada em Washington em outubro de 1884, foi definida como variando de 0 a +180° (Leste de Greenwich) e de 0 a -180° (Oeste). Na convenção usada em astronomia, varia entre -12h (Oeste) e +12h (Leste), usando a conversão de 15°=1 hora, devido à rotação da Terra em um dia (360°/24 h=15°/h).
  
  

• latitude geográfica (Φ): ângulo medido ao longo do meridiano do lugar, com origem no equador e extremidade no zênite do lugar. Varia entre -90° e +90°. O sinal negativo indica latitudes do hemisfério sul e o sinal positivo hemisfério norte.
  
  
• Definição astronômica de latitude: A latitude de um lugar é igual à altura do pólo elevado (h_P).
  

As coordenadas geográficas não são iguais às magnéticas. O polo norte magnético foi definido em 1600 pelo físico e matemático inglês Sir William Gilbert (1544-1603) como o ponto onde o campo aponta na vertical. Entretanto o campo geomagnético não é um simples dipolo, o que faz com que o polo magnético médio não seja igual ao polo geomagnético, e muda com o tempo devido à mudanças no núcleo da Terra. Em 2024, o polo norte geomagnético esta localizado em latitude 85,958° N e longitude 141,945° O (na costa ao norte do Canadá), movendo-se entre 37 e 72 km/ano enquanto o polo sul geomagnético está localizado em latitude 63,897 S e longitude 135,221 L, entre a Antártica e a Austrália, movendo-se entre 5 e 9 km/ano.

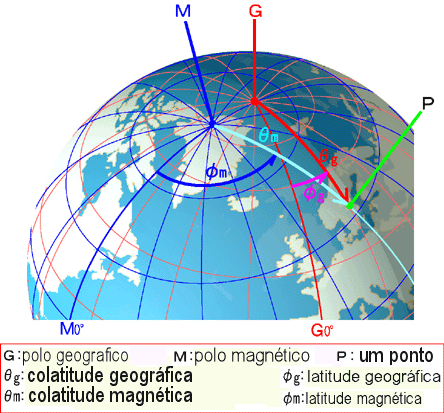
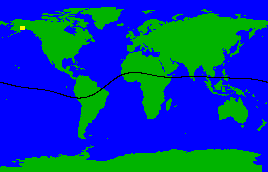equador geomagnético.

Coordenadas Astronômicas

Foto tirada pela espaçonave Clementina, mostrando a Lua, a coroa do Sol nascendo atrás da Lua, e os planetas Saturno, Marte e Mercúrio.

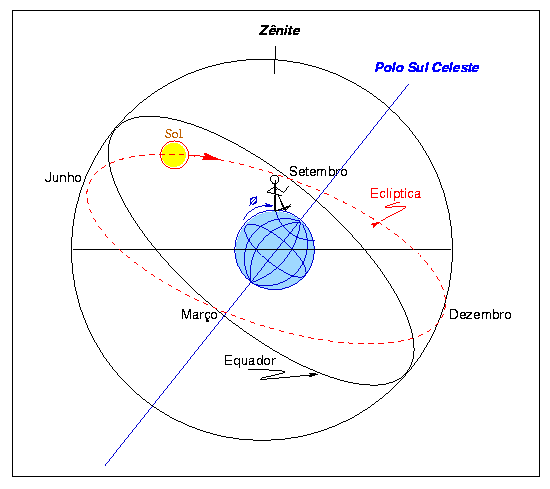
O plano da eclíptica é o plano imaginário contendo a órbita da Terra em volta do Sol e está inclinado 23,5° em relação ao equador. Durante o ano, a posição aparente do Sol está neste plano, assim como todos os planetas estão próximos deste plano, pois foram formados no disco proto-planetário.

O Sistema Horizontal

O Sistema Horizontal utiliza como plano fundamental o Horizonte celeste. As coordenadas horizontais são azimute e altura.

• Azimute (A): é o ângulo medido sobre o horizonte, no sentido horário (NLSO), com origem no Norte geográfico e extremidade no círculo vertical do astro. O azimute varia entre 0° e 360°.
  0° ≤ A ≤ 360°

• Altura (h): é o ângulo medido sobre o círculo vertical do astro, com origem no horizonte e extremidade no astro. A altura varia entre -90° e +90°. O complemento da altura se chama distância zenital (z). Assim, a distância zenital é o ângulo medido sobre o círculo vertical do astro, com origem no zênite e extremidade no astro. A distância zenital varia entre 0° e 180°:
  (h + z=90°)
  -90° ≤ h ≤ +900°
  0° ≤ z ≤ 180°

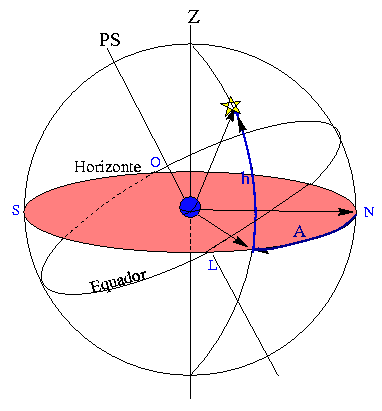
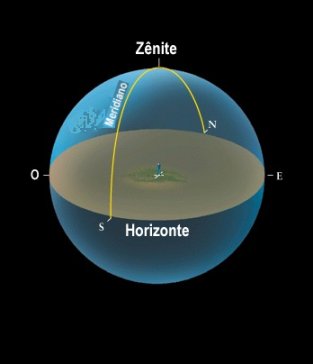
O sistema horizontal é um sistema local, no sentido de que é fixo na Terra. As coordenadas azimute e altura (ou azimute e distância zenital) dependem do lugar e do instante da observação, e não são características do astro.

O Sistema Equatorial Celeste

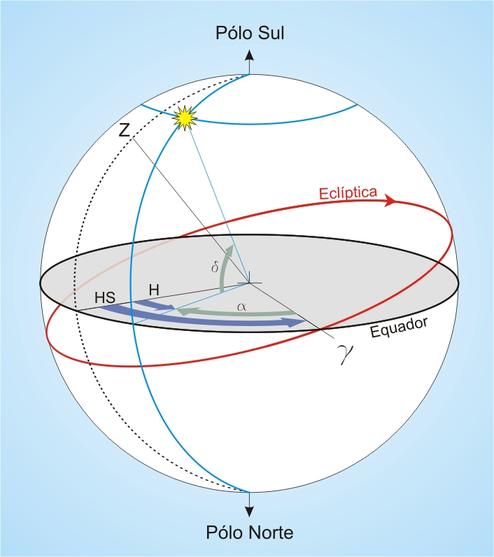
O Sistema Equatorial Celeste utiliza como plano fundamental o Equador celeste, projeção do equador da Terra ao céu. Suas coordenadas são a ascensão reta e a declinação.

• Ascensão reta (α ou AR): ângulo medido sobre o equador, com origem no meridiano que passa pelo Ponto de Áries, e extremidade no meridiano do astro. A ascensão reta varia entre 0h e 24h (ou entre 0° e 360°) aumentando para leste.
  0h ≤ α ≤ 24h

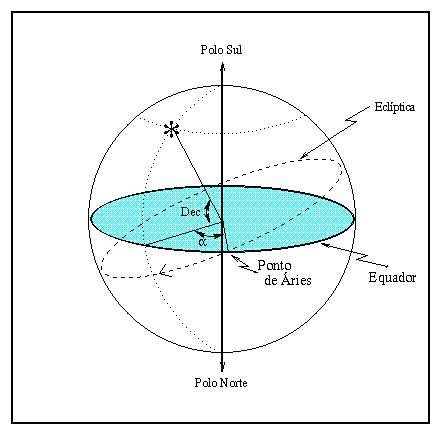
  O Ponto de Áries, também chamado Ponto Gama (), ou Ponto Vernal, é um ponto do equador, ocupado pelo Sol no equinócio de primavera do hemisfério norte, isto é quando o Sol cruza o equador vindo do hemisfério sul (geralmente em 22 de março de cada ano). Estava na constelação de Áries há dois mil anos.

• Declinação (δ): ângulo medido sobre o meridiano do astro (perpendicular ao equador), com origem no equador e extremidade no astro. A declinação varia entre -90° e +90°. O complemento da declinação se chama distância polar Δ (δ + Δ=90°).
  -90° ≤ δ ≤ +90°

O sistema equatorial celeste é fixo na esfera celeste e, portanto, suas coordenadas não dependem do lugar e instante de observação. A ascensão reta e a declinação de um astro permanecem praticamente constantes por longos períodos de tempo (veja Precessão).

Sistema Equatorial Horário

Nesse sistema o plano fundamental continua sendo o Equador, mas a coordenada medida ao longo do equador não é mais a ascensão reta, e sim uma coordenada não constante chamada ângulo horário. A outra coordenada continua sendo a declinação.

• ângulo horário (H): ângulo medido sobre o equador, com origem no meridiano local e extremidade no meridiano do astro. Varia entre -12h e +12h. O sinal negativo indica que o astro está a leste do meridiano, e o sinal positivo indica que ele está a oeste do meridiano.

-12h ≤ H ≤ +12h

Tempo Sideral

O sistema equatorial celeste e o sistema equatorial horário, juntos, definem o conceito de tempo sideral. O tempo sideral, assim como o tempo solar, é uma medida do tempo, e aumenta ao longo do dia.

• Hora sideral (HS): ângulo horário do ponto Áries. Pode ser medida a partir de qualquer estrela, pela relação: HS=H_* + α_*
  
• Dia Sideral: é o intervalo de tempo decorrido entre duas passagens sucessivas do ponto γ pelo meridiano do lugar (Sul-Zênite-Norte).
  
• Dia Solar: é o intervalo de tempo decorrido entre duas passagens sucessivas do Sol pelo meridiano do lugar. É 3^m56^s mais longo do que o dia sideral. Essa diferença é devida ao movimento de translação da Terra em torno do Sol, de aproximadamente 1 grau (4 minutos) por dia (360°/ano=0,986°/dia). Como a órbita da Terra em torno do Sol é elíptica, a velocidade de translação da Terra em torno do Sol não é constante, causando uma variação diária de 1° 6' (4^m27^s) em dezembro, e 53' (3^m35^s) em junho.
  

Movimento Diurno dos Astros

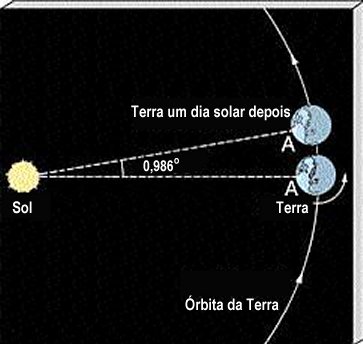
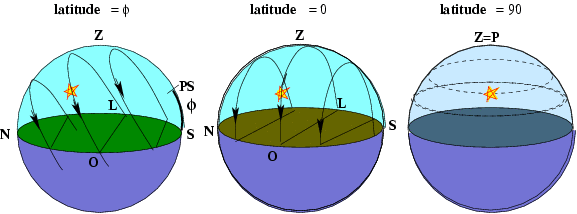
O movimento diurno dos astros, de leste para oeste, é um reflexo do movimento de rotação da Terra, de oeste para leste. Ao longo do dia, todos os astros descrevem no céu arcos paralelos ao Equador. A orientação desses arcos em relação ao horizonte depende da latitude do lugar.

• 1. Nos pólos (Φ=±90°): Todas as estrelas do mesmo hemisfério do observador permanecem 24 h acima do horizonte (não têm nascer nem ocaso), e descrevem no céu círculos paralelos ao horizonte. As estrelas do hemisfério oposto nunca podem ser vistas.

• 2. No equador (Φ=0): Todas as estrelas nascem e se põem, permanecendo 12h acima do horizonte e 12h abaixo dele. A trajetória das estrelas são arcos perpendiculares ao horizonte. Todas as estrelas do céu (dos dois hemisférios) podem ser vistas ao longo do ano.

• 3. Em um lugar de latitude intermediária: Algumas estrelas têm nascer e ocaso, outras permanecem 24h acima do horizonte, outras permanecem 24h abaixo do horizonte. As estrelas visíveis descrevem no céu arcos com uma certa inclinação em relação ao horizonte, a qual depende da latitude do lugar.

Passagem Meridiana de um Astro

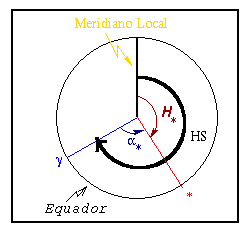
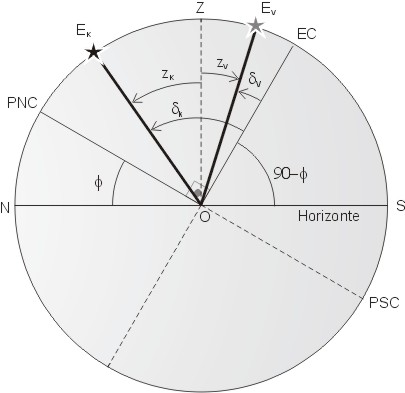Chama-se passagem meridiana ao instante em que o astro cruza o meridiano local. Durante o seu movimento diurno, o astro realiza duas passagens meridianas, ou duas culminações: a culminação superior, ou passagem meridiana superior, ou ainda máxima altura (porque nesse instante a altura do astro atinge o maior valor), e a passagem meridiana inferior, ou culminação inferior.

No instante da passagem meridiana superior,
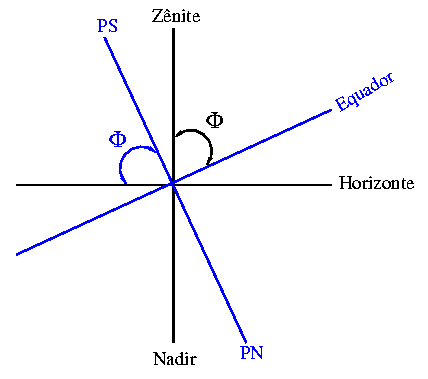
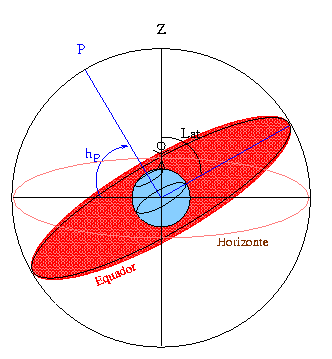
Φ=δ_k-z_k ou
Φ=δ_v+z_v,
já que o ângulo entre o equador celeste (EC) e o zênite (Z) é a latitude do local, Φ, ou seja, cumpre-se a seguinte relação entre a distância zenital z, a declinação δ, e a latitude do local Φ:

$z = \pm (\delta - \phi)$

onde o sinal + vale se a culminação é feita ao norte do zênite (z_K) e o sinal - se a culminação é feita ao sul do zênite (z_V).
Por exemplo, a galáxia de Andrômeda tem declinação de +41°. Em Porto Alegre, com latitude -30°, qual é sua altura máxima? Pela relação anterior, obtemos que sua distância zenital é de z=±[41-(-30)]°=±71°. Como a altura é o complemento da distância zenital, a altura na passagens meridiana é 90°-71°=19°, pois ela passa ao norte do zênite. Portanto, a altura máxima é 19°. Como esta galáxia tem ascenção reta próxima de 0h, qual é a melhor época para observá-la? Por definição, o Sol está com AR=0h próximo de 20 de março. A melhor época para observer um objeto celeste com AR=0h é 6 meses depois, quando o Sol está em 12h e, portanto, à meia noite a AR=0h passa pelo meridiano superior.

Estrelas Circumpolares

Estrelas circumpolares são aquelas que não têm nascer nem ocaso, descrevendo seu círculo diurno completo acima do horizonte. Portanto, as estrelas circumpolares fazem as duas passagens meridianas acima do horizonte. Para uma certa estrela com declinação δ ser circumpolar em um lugar de latitude Φ deve se cumprir a relação:

com δ e Φ de mesmo sinal.

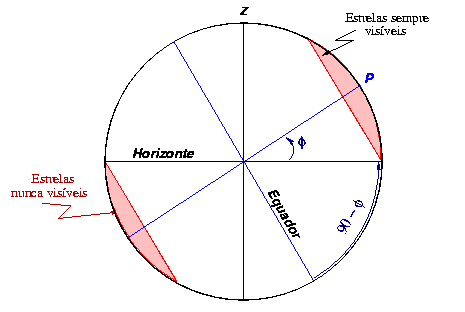
Por exemplo, a estrela mais brilhante da constelação do Cruzeiro do Sul (Acrux, α Crucis) tem declinação de -65°. Em Porto Alegre, como a latitude é -30°, essa relação indica:

|65 °| $\geq$ 90°-|30°| = 60°

verdadeiro porque tanto a declinação quanto a latitude têm o mesmo sinal, negativo neste caso. Essa estrela é circumpolar em Porto Alegre, isto é, está sempre acima do horizonte. A estrela Polar, que está próxima ao Polo Norte, nunca é visível para latitudes Sul.

Para derivar as relações entre os sistemas de coordenadas, é necessário utilizar-se a Trigonometria Esférica, também detalhada no hipertexto de Geodésica.

Nenhuma projeção de uma esfera em um plano é perfeita. A projeção de Mercator, proposta por Gerhardus Mercator in 1569, é sobre um plano (x,y), com coordinadas: x = λ, e y = ln[tan(π/4 + φ/2)], onde φ é a latitude, em radianos, e λ a longitude, em radianos.

Questionário e Auto Teste

Simulação em Java de Walter Fendt: Polo Celeste e Posição das Estrelas
Calcule o melhor dia para observar um objeto

Posições do Sol
Astronomia e Astrofísica