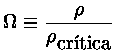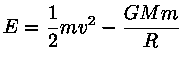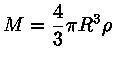A Densidade Crítica do Universo
A
velocidade de escape
é definida como:
e a Lei de Hubble é:
Definindo a densidade equivalente à
velocidade de escape como
aquela correspondente à densidade crítica:
obtemos:
ou
A abundância observada de deutério, e também a de hélio,
indicam que a densidade bariônica (de matéria normal) não
pode ser maior do que 0,1 da densidade crítica. Entretanto
o movimento das galáxias em cúmulos de galáxias requer
que a densidade total seja pelo menos 0,2 da densidade crítica.
Parte da matéria escura precisa ser exótica.
Portanto sabemos que a densidade de matéria (e energia) atualmente
é próxima da densidade crítica, mas
não existe evidência observacional de que a densidade
total seja igual à densidade crítica.
Problema da Planicidade
Entretanto, temos o problema da planicidade (flatness problem),
se o Universo não for plano.
Suponha que
em um certo momento do Universo a densidade de matéria
seja 0,5 da densidade crítica. Quando o Universo
se expande por um fator de 2, a densidade crítica
diminui por um fator de 4, pois depende de
H2 e
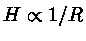 para energia total não nula,
mas a densidade de matéria
diminui por um fator de 8, pois depende de
para energia total não nula,
mas a densidade de matéria
diminui por um fator de 8, pois depende de
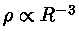 .
Estamos usando r=R, a distância entre as galáxias. Logo
.
Estamos usando r=R, a distância entre as galáxias. Logo
diminui de 0,5 para 0,25 quando o Universo se expande por um fator de 2.
Como o Universo se expandiu por um fator de 1000
desde que sua temperatura era de 3000 K, a
época da recombinação (captura dos elétrons
formando átomos), o fato da densidade atual
ser próxima da densidade crítica indica
que era igual a 1 mais próximo do que uma parte em 1000
naquela época, e muito mais próximo de 1 ainda
para épocas anteriores.
Por exemplo, quando o Universo tinha 1 segundo,
época do início das reações
nucleares, a igualdade é de uma parte em
1015, e para 1 nanosegundo,
10-9 segundos, a igualdade é
de uma parte em 1047.
Portanto nosso Universo
iniciou com a energia cinética muito próximo
da energia gravitacional, levando à suspeita
de que a densidade deve ser exatamente
igual à densidade crítica, isto é,
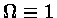 ,
que é um Universo plano. Neste caso a
densidade crítica também depende de R-3.
De outra maneira seria apenas uma mera coincidência que
nós estejamos observando justamente quando a
diferença da planicidade começa a ser significativa.
Se o Universo é plano então a energia total
é nula, e uma pequena flutuação
estatística da energia do vácuo poderia
formar toda a matéria (1080 partículas)
existentes no Universo.
Flutuações quânticas no vácuo podem
vir de flutuações dos campos dos bósons,
dos infinitos níveis de energia negativa dos férmions,
o chamado mar de Dirac, e ainda de algumas teorias dos
campos de Higgs, que podem ter energia negativa ou positiva.
Os modelos inflacionários predizem
,
que é um Universo plano. Neste caso a
densidade crítica também depende de R-3.
De outra maneira seria apenas uma mera coincidência que
nós estejamos observando justamente quando a
diferença da planicidade começa a ser significativa.
Se o Universo é plano então a energia total
é nula, e uma pequena flutuação
estatística da energia do vácuo poderia
formar toda a matéria (1080 partículas)
existentes no Universo.
Flutuações quânticas no vácuo podem
vir de flutuações dos campos dos bósons,
dos infinitos níveis de energia negativa dos férmions,
o chamado mar de Dirac, e ainda de algumas teorias dos
campos de Higgs, que podem ter energia negativa ou positiva.
Os modelos inflacionários predizem 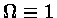 porque a expansão inflacionária é
tão gigantesca que qualquer que fosse a
geometria antes da inflação, ela é
plana após a expansão. Uma outra vantagem
da inflação é que ela ocorre
após a formação dos monopolos
magnéticos, preditos pelas teorias de Grande
Unificação e, portanto, dilui a
densidade destes para números muito pequenos.
porque a expansão inflacionária é
tão gigantesca que qualquer que fosse a
geometria antes da inflação, ela é
plana após a expansão. Uma outra vantagem
da inflação é que ela ocorre
após a formação dos monopolos
magnéticos, preditos pelas teorias de Grande
Unificação e, portanto, dilui a
densidade destes para números muito pequenos.
A energia total E
de uma galáxia de massa m
a uma
distância R, deslocando-se com velocidade v
em um campo gravitacional dado por uma massa M,
é dada por:
Usando-se a Lei de Hubble v=H R
e escrevendo a massa M
em função da densidade de massa:
podemos derivar
a equação de Friedmann:
para o caso geral de energia E.
Para matéria não relativística,
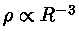 e o primeiro termo decresce mais rapidamente que o segundo
termo (termo de curvatura) e, portanto, o segundo domina para R grande.
Deste modo, se a energia
E
não for nula, H2 é proporcional a R-2.
Entretanto, se a densidade for igual à densidade crítica,
o primeiro termo domina sobre o termo de curvatura, que torna-se nulo, já que
E=0 se a velocidade for igual à velocidade de escape, por definição.
e o primeiro termo decresce mais rapidamente que o segundo
termo (termo de curvatura) e, portanto, o segundo domina para R grande.
Deste modo, se a energia
E
não for nula, H2 é proporcional a R-2.
Entretanto, se a densidade for igual à densidade crítica,
o primeiro termo domina sobre o termo de curvatura, que torna-se nulo, já que
E=0 se a velocidade for igual à velocidade de escape, por definição.
 Cosmologia
Cosmologia
Volta: Astronomia e Astrofísica
©
Modificada em 12 ago 2003
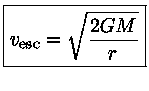
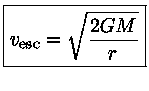
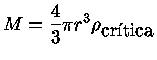
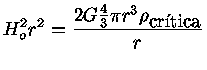
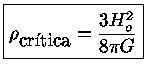
![]() para energia total não nula,
mas a densidade de matéria
diminui por um fator de 8, pois depende de
para energia total não nula,
mas a densidade de matéria
diminui por um fator de 8, pois depende de
![]() .
Estamos usando r=R, a distância entre as galáxias. Logo
.
Estamos usando r=R, a distância entre as galáxias. Logo