
| Tipos | Dispersão | Resolução | Grisma | Redução |
|---|
Na espectroscopia, os espectros são obtidos pela dispersão ou singularizarão das ondas de luz de uma fonte em seus diferentes comprimentos. Ou seja, a espectroscopia separara a contribuição dos diferentes comprimentos de onda provenientes de uma fonte.
Na espectroscopia, os espectros obtidos pela dispersão da luz permitem que obtenhamos o fluxo da fonte em função do comprimento de onda, F(λ).A
quantidade de informação existente em um espectro, F(λ),
é muito maior do que aquela de uma imagem, na
qual o espectro está integrado em um amplo domínio de
λ (λ1<λ<λ2)
e pesado pela função de transmissão do filtro
e telescópio, Φ(λ).
![]()
onde F(λo)
é o fluxo no comprimento de onda efetivo.
A função de transmissão Φ(λ) mede a fração da luz da fonte que é detectada em cada comprimento de onda.
A integração em comprimento de onda em uma imagem leva necessariamente a uma perda de informação, pois estamos obtendo um sinal integrado, sem saber a forma real do espectro da fonte. Com espectros estelares, por exemplo, podemos determinar as condições físicas e químicas na atmosfera das estrelas, como temperatura, gravidade superficial, ventos estelares, composição química, etc., algo que é muito menos preciso quando temos apenas medidas fotométricas em algumas bandas, ou seja, magnitudes e cores.
Em compensação, é mais fácil detectar sinal em um detector somando-se as contribuições dentro de um domínio de comprimentos de onda. Ou seja, é necessário mais tempo de exposição para construirmos uma dada razão sinal/ruído para cada λ individualmente.
E esse compromisso entre a quantidade de informação obtida e a rapidez com que se obtém o sinal que carrega essa informação que faz da fotometria e da espectroscopia técnicas complementares e amplamente utilizadas.
A refração da luz foi estudada em 1621 pelo matemático e físico holandês Willebrord Snell (1591-1626) e descrita pelo filósofo francês René Descartes (1596-1650) no seu livro Dioptrics de 1637. Já no primeiro artigo de Isaac Newton (1642-1726) em 1672, no Philosophical Transactions of the Royal Society, 6, 3075, e no Lectures opticae de 1669 na Universidade de Cambridge, ele descreve como usou um prisma para dispersar a luz e separá-la em suas cores, explicando o arco-iris. Depois observou Vênus e estrelas de primeira magnitude, observando o espectro contínuo. Newton descreveu que o poder dispersivo do prisma estava relacionado com o índice de refração do vidro.
Em 1801, Thomas Young (1773-1809) foi o primeiro a usar uma rede de difração, com 500 linhas por polegada, e observando as quatro primeiras ordens da luz do Sol dispersada, encontrou senβ ∝ n, n=1,2,3,..., onde β é o ângulo de difração, e estimou que o espectro visível ia de 424 nm a 675 nm (1802, Philosophical Society of the Royal Society, 92, 12).
 O fabricante de vidros alemão
Joseph von Fraunhofer (Frauenhofer)
(1787-1826) continuou as experiências com
redes de difração, construindo redes com até 300 linhas por mm e,
em uma série de artigos de 1817 a 1824
(Denkschriften der Münch Akademie der Wissenschaften, 5, 193;
Edinburgh Philosophical Journal, 10, 26)
usando telescópios de 2,5 a 10 cm de diâmetro,
contou 574 linhas escuras
no espectro solar, chamadas depois de linhas de Fraunhofer.
Para 324 destas linhas, Fraunhofer deu o nome de letras maiúsculas:
A, B, C ...
para as linhas mais fortes e minúsculas para as mais fracas,
começando com A no vermelho,
identificadas
com os elementos químicos em 1856 por
Gustav Robert Kirchhoff (1824-1887)
[Abhandlungen der Berliner Akademie Part I, p. 63 (1861),
p. 227 (1862), Part II, p. 225 (1863)].
O fabricante de vidros alemão
Joseph von Fraunhofer (Frauenhofer)
(1787-1826) continuou as experiências com
redes de difração, construindo redes com até 300 linhas por mm e,
em uma série de artigos de 1817 a 1824
(Denkschriften der Münch Akademie der Wissenschaften, 5, 193;
Edinburgh Philosophical Journal, 10, 26)
usando telescópios de 2,5 a 10 cm de diâmetro,
contou 574 linhas escuras
no espectro solar, chamadas depois de linhas de Fraunhofer.
Para 324 destas linhas, Fraunhofer deu o nome de letras maiúsculas:
A, B, C ...
para as linhas mais fortes e minúsculas para as mais fracas,
começando com A no vermelho,
identificadas
com os elementos químicos em 1856 por
Gustav Robert Kirchhoff (1824-1887)
[Abhandlungen der Berliner Akademie Part I, p. 63 (1861),
p. 227 (1862), Part II, p. 225 (1863)].

Fraunhofer também observou linhas nos espectros das estrelas
Sírius, Castor, Pollux, Capella, Betelgeuse e Procyon.
Ela já usava uma fenda para definir as linhas, que são diretamente imagens
da fenda em cada comprimento de onda.
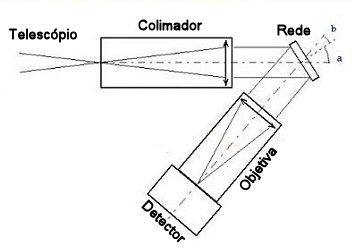
Os primeiros controles de temperatura e flexão foram feitos por William Wallace Campbell (1862-1938) (1898, Astrophysics Journal, 8, 123), no Observatório Lick (Califórnia) e Henri Alexandre Deslandres (1853-1948) (1898, Bulletin Astronon., 15, 49), no Observatório de Paris. Tanto flexão quanto variações de temperatura podem causar deslocamentos nas linhas durante a exposição, com o telescópio em movimento, borrando as linhas e levando a erros na determinação de centro e forma da linha. A variação de temperatura causa mudanças no índice de refração do prisma, e é uma consideração importante por causa das variações de temperatura durante a noite. Johannes Franz Hartmann (1865-1936), de Postdam, já tinha determinado uma mudança da ordem de 0,3 Å/C em Hγ, para prismas de quartzo cristalino (flint), que corresponde a uma velocidade radial de 20 km/s/C. Para comparar, lembre que o efeito de Júpiter sobre o Sol é de 12 m/s.
Uma maneira de aumentar a resolução de um espectrógrafo é aumentar a distância entre a objetiva e o detector. O desenvolvimento do espectrógrafo coudé (dobrado) foi feito por Maurice Loewy (1833-1907), em Paris (1883, Comptes Rendus de l'Academie de Sciences, Paris, 96, 735), para um telescópio refrator de 27 cm, com dois espelhos de 45° enviando a luz pelo eixo polar. O primeiro espectrógrafo coudé em um telescópio refletor foi projetado por George Ellery Hale (1868-1938) (1912, Publications of the Astronomical Society of the Pacific, 24, 223) e Walter Adams (1876-1956), no Mount Wilson 60" (1,5 m) (1911, Astrophysical Journal, 35, 163), com um prisma de 63°. O espectrógrafo coudé foi desenvolvido para aumentar a resolução, aumentando a distância focal, sem ser dominado pela flexão no colimador. Colocando-se espelhos no eixo do telescópio, aumenta-se a distância focal e, portanto, a resolução, sem flexão, mas aumenta-se também a perda de luz pelas reflexões. Por exemplo, se tivermos 6 reflexões antes da luz incidir sobre a rede, considerando uma refletividade de 0,88 para um espelho recém coberto de alumínio, no visual, e uma eficiência de rede com blazing (brilhança) de 70%, obtemos que menos de 0,886×0,7=0,33 da luz incidente chega ao detector. Mas atualmente se consegue uma refletividade de mais de 97,5% em regiões limitadas do espectro. Espelhos com coberturas (coating) diferentes são necessários para cada região espectral.


O espectrógrafo com câmera acromática foi desenvolvido pelo astrônomo alemão Johannes Franz Hartmann (1865-1936) em 1904, e as redes com maior eficiência em uma única ordem (blazing, brilhança, com linhas em ângulo - inclinadas um ângulo apropriado em relação à normal para direcionar a maior parte da luz em uma única ordem, e com formato V) por Clement Jacomini (1856-1940) em 1929 e Robert W. Wood (1868-1955) em 1936 (1937, Nature, 140, 723).
Os meios responsáveis pela dispersão da luz podem ser um prisma ou uma rede de difração. Alternativamente, pode-se singularizar um dado λ (ou conjunto de λs) pelo uso de um interferômetro, como o Brazilian Tunable Filter Imager. Discutiremos esse elementos de dispersão mais adiante.
Em sua
forma mais rudimentar, a espectroscopia faz a luz que incide sobre o plano
focal de um telescópio (ou parte dela) passar por um ou mais
elemento dispersor
antes de chegar a um detector.
Dessa forma, a imagem de cada objeto no detector é substituída
por um espectro. Obtemos, portanto, uma imagem de espectros,
tal como mostrado na figura, obtida como parte de um projeto de classificação espectral de estrelas
(Coryn A. L. Bailer-Jones, Mike Irwin & Ted von Hippel,
1998, Monthly Notices of the Royal
Astronomical Society, 298, 1061).
 Essa técnica
é chamada de
prisma objetivo ou espectroscopia sem fenda. Em geral, os
espectros resultantes da dispersão por um prisma são de baixa dispersão,
ou seja, um grande intervalo dλ
é espalhado
em um ângulo pequeno dθ
(dλ/dθ é grande).
Se os espectros forem de alta dispersão, os vários
espectros formados, dispersos sobre a imagem, tenderão a se superpor,
confundindo a sua analise.
Karl Schwarzchild (1873-1916) publicou em 1913, Publikation der astrophysikalischen Observatoriums Postdam,
23 (Nr 69), 1, a análise teórica do observação com
prisma objetivo.
Essa técnica
é chamada de
prisma objetivo ou espectroscopia sem fenda. Em geral, os
espectros resultantes da dispersão por um prisma são de baixa dispersão,
ou seja, um grande intervalo dλ
é espalhado
em um ângulo pequeno dθ
(dλ/dθ é grande).
Se os espectros forem de alta dispersão, os vários
espectros formados, dispersos sobre a imagem, tenderão a se superpor,
confundindo a sua analise.
Karl Schwarzchild (1873-1916) publicou em 1913, Publikation der astrophysikalischen Observatoriums Postdam,
23 (Nr 69), 1, a análise teórica do observação com
prisma objetivo.
Mais comum em astronomia é a espectroscopia de fenda única, em que apenas a luz que atravessa uma fenda longa posicionada no plano focal do telescópio é selecionada antes de ser dispersada e registrada em um detector. Na espectroscopia de fenda longa é naturalmente muito mais fácil selecionar as fontes a serem dispersas, pois a fenda serve como sistema que só deixa passar a luz daquela(s) fonte(s). Assim, o espectro obtido com uma fenda longa pode ser de alta dispersão (baixos valores de dλ/dθ). Note que a espectroscopia de fenda longa preserva a informação espacial das fontes ao longo da fenda. Ou seja, o plano do detector tem uma direção de dispersão da luz, perpendicular à fenda, e outra, espacial, ao longo da mesma.

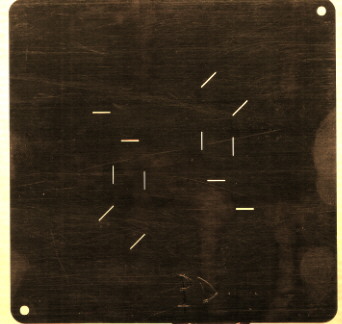

No modo de espectroscopia multi-fenda (MOS - multi object spectrograph) são cortadas várias fendas em uma placa metálica, a qual é posicionada na superfície focal do telescópio. As posições das fendas coincidem com as das fontes cujos espectros desejamos obter. A luz dessas fontes que atravessa cada fenda individualmente é então dispersa, em geral por uma rede de difração, e direcionada, por meio de um sistema óptico à entrada de uma câmera CCD, onde os espectros resultantes são então dispostos ordenadamente. Assim, é possível coletar simultaneamente vários, às vezes centenas, de espectros de fontes situadas no campo do telescópio. Este método foi primeiro usado por Harvey Butcher (1947-) no Kitt Peak em 1980 (Proceedings of the Society of Photo-instrumentation Engineers (SPIE), 331, 296, 1982) e automatizado no CHFT (B. Fort, Y. Mellier, J.P. Picet, Y. Rio & G. Lelievre, 1986, Proceedings of the Society of Photo-instrumentation Engineers (SPIE), 627, 321) e ESO (B. Buzzoni, B. Delabre, H. Dekker et al., 1987, European Southern Observatory Messenger, 47, 55).
O espectrógrafo BOSS do Sloan Digital Sky Survey utiliza um sistema de multi-fendas, com 1000 fendas (640 fendas no espectrógrafo do SDSS I e II) em cada placa de alumínio, que alimentam o espectrógrado através de fibras óticas de 2 segundos de arco (3" no SDSS I e II). Os espectros do SDSS vão de 3600Å (azul) a 10500Å (infravermelho próximo) (3800Å a 9200Å no I e II) (1 Å=10-10m). A luz de cada objeto passa por um separador de feixes antes de ser enviada aos espectrógrafos, um para a parte vermelha e outro para a parte azul, e são imageados em dois CCDs de 4096×4096 pixeis. Em junho de 2017 ocorreu a décima quarta liberação de dados (data release) do SDSS, com 4,8 milhões de espectros.
O primeiro data release do LAMOST (Large Sky Area Multi-Object Fiber Spectroscopic Telescope) do Guo Shou Jing Telescope, um Schmidt com 6 m de espelho primário e 4 m efetivo, com 4000 fibras cobrindo um campo de 5°, ocorreu em 20 de agosto de 2012, com 493 000 espectros com S/R>10 de objetos com 13<g<20.5 mag, imageados em 32 cameras usando CCDs EEV de 4096×4096, com R=1800. O DR3, em junho de 2017 tem mais de 5,7 milhões de espectros de estrelas.

Outro sistema de espectroscopia multi-objetos usa um espectrógrafo que posiciona extremidades de fibras ópticas na superfície focal do telescópio, sendo que as outras extremidades das fibras, pelas quais se dá a saída da luz coletada, encaminham a luz ao sistema de dispersão e detecção do espectro.


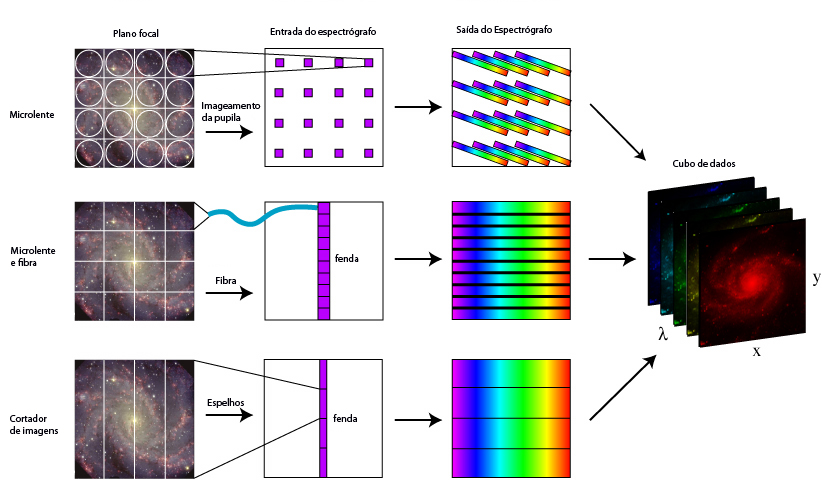
O SIFS (Soar Integral Field Spectrograph), construído pelo Laboratório Nacional de Astrofísica e Instituto Astronômico e Geofísico da Universidade de São Paulo, coordenado por Clemens Gneiding, Jacques Lépine e Beatriz Barbuy, tem 1300 fibras, operando de 3200 a 8 000 Å, com R=5000 a 20 000, cobrindo um campo de 8″×15″, com microlentes de 0,30″. Opera com 5 redes VPH (Volume Phase Holographic grating).
 Em 1949 o americano George Russell Harrison
(1898-1979) desenvolveu a rede échelle, com
alto ângulo de blazing
(Journal Optical Society of America, 39, 522),
que levou à construção dos espectrógrafos échelle,
em 1951 por
A. Keith Pierce
(1918-2005),
Robert R. McMath
(1891-1962)
e Orren Mohler (1908-1985), na Universidade de Michigan, para espectroscopia
solar, com uma resolução R=λ/Δλ=250 000 (Astronomical Journal, 56, 137).
A partir de 1965, espectrógrafos échelles foram desenvolvidos
para os focos coudé e Nasmyth
[Ivan
Mikheevich Kopylov (1928-2000) & Nikolay V. Steshenko,
1965, Proceedings of the Crimean Astrophysics Observatory, 33, 308;
Y. Fujita, 1966, Vistas in Astronomy, 7, 71).
Em 1967, Daniel Schroeder (1933-) (Applied Optics, 6, 1976)
desenvolveu um espectrógrafo Cassegrain échelle para um telescópio
pequeno, o 91 cm da Universidade de Wisconsin.
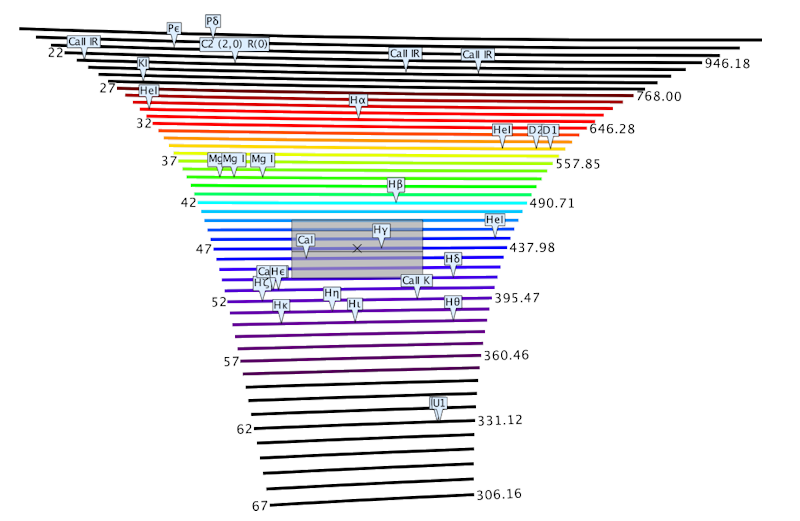
Diferente das redes com a maior parte da luz em uma única ordem,
as redes échelles têm número de linhas pequeno, tipicamente 31,6
ou 79 linhas/mm, operando simultaneamente em várias ordens
(cerca de 100 ordens para a rede de 31,6 linhas/mm e cerca de 40 ordens
para a rede com 79 linhas/mm).
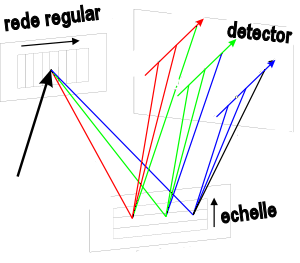
A separação de ordens é feita com um prisma, grisma ou rede
de difração convencional, produzindo uma pequena dispersão na
direção ortogonal àquela da rede échelle
(Simulador
de ordens no Keck).
Em 1949 o americano George Russell Harrison
(1898-1979) desenvolveu a rede échelle, com
alto ângulo de blazing
(Journal Optical Society of America, 39, 522),
que levou à construção dos espectrógrafos échelle,
em 1951 por
A. Keith Pierce
(1918-2005),
Robert R. McMath
(1891-1962)
e Orren Mohler (1908-1985), na Universidade de Michigan, para espectroscopia
solar, com uma resolução R=λ/Δλ=250 000 (Astronomical Journal, 56, 137).
A partir de 1965, espectrógrafos échelles foram desenvolvidos
para os focos coudé e Nasmyth
[Ivan
Mikheevich Kopylov (1928-2000) & Nikolay V. Steshenko,
1965, Proceedings of the Crimean Astrophysics Observatory, 33, 308;
Y. Fujita, 1966, Vistas in Astronomy, 7, 71).
Em 1967, Daniel Schroeder (1933-) (Applied Optics, 6, 1976)
desenvolveu um espectrógrafo Cassegrain échelle para um telescópio
pequeno, o 91 cm da Universidade de Wisconsin.
Diferente das redes com a maior parte da luz em uma única ordem,
as redes échelles têm número de linhas pequeno, tipicamente 31,6
ou 79 linhas/mm, operando simultaneamente em várias ordens
(cerca de 100 ordens para a rede de 31,6 linhas/mm e cerca de 40 ordens
para a rede com 79 linhas/mm).
A separação de ordens é feita com um prisma, grisma ou rede
de difração convencional, produzindo uma pequena dispersão na
direção ortogonal àquela da rede échelle
(Simulador
de ordens no Keck).
 Nos anos 1960 as redes holográficas (VPH) foram produzidas por
vários grupos, com a interferência de lasers monocromáticos,
mas somente em 1998 Sam Barden, James A. Arns e Willis S. Colburn
(Proceedings of the Society of Photo-Instrumentation
Engineers, SPIE, 3355, 866) propuseram
seu uso astronômico, e hoje são usadas por exemplo no
espectrógrado Goodman do Soar, construído por
J. Christopher Clemens,
com altíssima eficiência, pois opera no regime de
Bragg
[Sir
William Henry Bragg (1862-1942)], prêmio
Nobel com seu filho
Sir
William Lawrence Bragg (1890-1971)],
onde a maior parte da potência difratada está em uma
única ordem.
Nos anos 1960 as redes holográficas (VPH) foram produzidas por
vários grupos, com a interferência de lasers monocromáticos,
mas somente em 1998 Sam Barden, James A. Arns e Willis S. Colburn
(Proceedings of the Society of Photo-Instrumentation
Engineers, SPIE, 3355, 866) propuseram
seu uso astronômico, e hoje são usadas por exemplo no
espectrógrado Goodman do Soar, construído por
J. Christopher Clemens,
com altíssima eficiência, pois opera no regime de
Bragg
[Sir
William Henry Bragg (1862-1942)], prêmio
Nobel com seu filho
Sir
William Lawrence Bragg (1890-1971)],
onde a maior parte da potência difratada está em uma
única ordem.
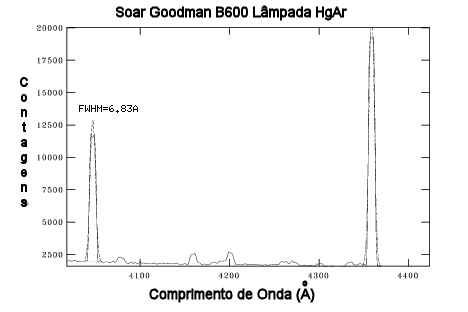
As redes VPH têm uma camada de gelatina na qual o índice de refração muda nas linhas na rede, produzido por regiões de diferentes índices de refração. Como operam no limite de Bragg, sua eficiência chega a 95% em primeira ordem. Podem operar tanto em transmissão quanto em reflexão. O espectrógrafo Goodman, do Soar, opera de 3200 a 8500 Å, com R=λ/Δλ=1400 (rede de 300 linhas/mm com fenda de 0,45″) a 10100 (rede de 2100 linhas/mm com fenda de 0,45″), e imageamento em um campo de 7,2′×7,2′, sobre um CCD Fairchild 4096×4096 pixeis, com 15 μm/pixel (0,15″/pixel). A eficiência total do Goodman, com a rede de 2100 l/mm, é de 29%, e a resolução de 0,17 Å/pixel, cobrindo cerca de 700 Å. Existe interferência no CCD (fringing) acima de 6500Å com o CCD azul (blue camera).
O espectrógrafo echelleSTELES (SOAR Telescope Echelle Spectrograph) foi construído pelo LNA para o Soar, opera de 3000Å a 8900Å em uma só exposição, com uma rede echelle R4 e 2 CCDs de 4096×2048. A eficiência total projetada é de 5% em 3000Å e 15% de 3800Å a 8000Å e R=50 000, similar ao ECHARPE, para o 1,6 do Observatório do Pico dos Dias.
O Ohio State InfraRed Imager/Spectrometer (OSIRIS) não está mais sendo oferecido no SOAR. Tem um detector de 1024×1024 píxeis, com modos de baixa-resolução (R~1200) e alta-resolução (R~3000) em fenda longa, e um mode de baixa resolução de dispersão cruzada de fenda curta, operando de 1,0 a 2,2 μm.
No Gemini, o principal espectrógrafo ótico é o GMOS (Gemini Multiobject Spectrograph), com uma versão no Gemini Sul optimizada no azul (27% em 5700 Å com a rede B600)e no Gemini Norte optimizada no vermelho (28% em 7000 Å com a R831). No Gemini Sul é possível orientar a fenda no ângulo paralático. Os GMOS operam de 3600 Å a 9400 Å no modo de fenda longa e de multi-fendas (máscaras cortadas a laser), obtendo espectroscopia e imageamento em um campo de 5,5 minutos de arco. Cada GMOS tem também uma Unidade de Campo Integral, que pode obter espectros de uma área de 35 segundos de arco, com resolução espacial de 0,2 segundos de arco (fibras). Veja na página de instrumentos do Gemini os espectrógrafos infra-vermelho disponíveis. No Gemini norte temos o imageador NIRI (1 a 5μm, com espectroscopia grisma, 1024×1024 InSb - antimoneto de índio), o espectrógrafo de campo integral NIFS (1 a 2,5 μm 2048×2048 HgCdTe), o espectrógrafo com fenda longa do Gemini Norte (1 a 5μm, 1024×1024 InSb) e com dispersão cruzada GNIRS (0,9 a 2,5 μm, Aladdin III InSb), enquanto no Gemini Sul temos o espectrógrafo de alta resolução Phoenix (1 a 5μm, 1024×1024 InSb), e o espectrógrafo multi-objeto Flamingos-2 (0,95 a 2,4 μm 2048×2048 HgCdTe).
No CFHT temos o ESPaDOnS: Echelle SpectroPolarimetric Device for the Observation of Stars, com R=68 0000 de 370 a 1050 nm.
Em La Silla, no telescópio de 3,6 m do ESO, o espectrógrafo échelle HARPS, High Accuracy Radial velocity Planet Searcher cobre de 378 nm a 691 nm, R=115 0000 e, observando simultaneamente com uma lâmpada de Th-Ar, alcança precisão de 0,9 m/s.
A página de instrumentos do ESO Paranal lista os instrumentos disponíveis no observatório de Cerro Paranal, onde estão os VLTs, como o FORS2, FOcal Reducer/low dispersion Spectrograph 2 com R=260 a 2600 de 3300 Å a 1,1 μm, o UVES um espectrógrafo echelle de dispersão cruzada que opera desde o corte atmosférico de 3000 Å até o limite vermelho do CCD, próximo de 1,1 μm com R=80 000 a 110 000, e o XSHOOTER um espectrógrafo que observa simultaneamente do azul - 3000Å ao infravermelho - 2,5 μm, com R=3300 a 9100, além de vários espectrógrafos infravermelhos. O espectrógrafo echelle CRIRES cobre de 0,95 a 5,2 μm, com 4 detectores Aladdin (InSb) e 4096×512 pixeis. ISAAC é um imageador e espectrógrafo de 1 a 5 μm, com um detector 1024×1024 Hawaii Rockwell (HgCdTe 1-2,5 μm) e um 1024×1024 Aladdin (3 a 5 μm). SINFONI, um espectrógrafo de campo integral no infravermelho próximo (1,1 a 2,45 μm), com um detector Hawaii 2RG 2048×2048. KMOS, um espectrógrafo multi-objeto no infravermelho próximo (0,8 a 2,5 μm), com 24 IFUS e 3 Teledyne HgCdTe com substrato removido, 18 μm pixeis, Hawaii 2RG 2048×2048, com R=2000 a 4200. NaCo, imageador, polarímetro, coronógrafo e espectrógrafo assistido por ótica adaptativa, no ótico e infravermelho próximo (0,85 a 2,5 μm), com um detector Aladdin III (InSb - 1024×1026 pixeis)
A vantagem dos sistemas multi-objeto, seja por fendas ou diretamente por fibras é clara: a eficiência na geração de espectros. Por outro lado, nem sempre há, no campo do telescópio, fontes em número suficiente para terem seus espectros coletados e detectados em um CCD, por exemplo. Isso vai depender da abertura do telescópio, da razão focal (campo por ele coberto), da sensitividade do detector, e da densidade de fontes no campo. Além disso, a espectroscopia de fenda única e longa é adequada para obter espectros de objetos espacialmente resolvidos, como galáxias. Ao se alinhar a fenda com o eixo-maior de uma galáxia, por exemplo, obtemos espectros ao longo de todo o eixo, já que a fenda preserva a informação espacial em uma dimensão. A espectroscopia multi-objeto, por alinhar no detector espectros obtidos em diferentes posições no campo do telescópio, não mantém a informação espacial, sendo mais adequada para fontes pontuais. Na verdade, uma das maiores dificuldades da espectroscopia multi-objeto é manter a informação sobre a qual a fenda (ou fibra) que corresponde a cada espectro no detector, isto é, onde a fonte se situa no campo do telescópio.
Iniciemos a discussão levando em conta um sistema simples, que encerra em sua descrição todos os elementos e definições básicos das técnicas de espectroscopia, o prisma.
Este texto está baseado no capítulo 4 do livro Astrophysical Techniques, de Chris R. Kitchin, (4th Ed., 2003, Institute of Physics Publishing, Bristol and Philadelphia) e Astronomical Spectrographs and their History, de John Hearnshaw (2009, Cambridge University Press), e no texto Espectroscopia, de Basilio Santiago.
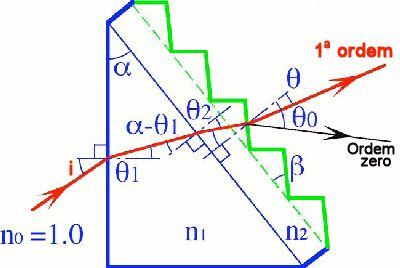
Nosso objetivo inicial é quantificar o desvio θ causado por um prisma sobre a luz de comprimento de onda λ que sobre ele incide. Sabemos, pela lei de Snell, proposta em 1621 por Willebrord Snell (1591-1626) e incluída por René Descartes (1596-1650) no seu livro Dioptrics de 1637, a relação entre os ângulos de incidência i e de refração r quando a luz atravessa o prisma a partir de um meio de índice de refração n1:
n1sen(i) = n2sen(r)
onde n2 é
o índice de refração do prisma, o qual varia com
λ .
A questão é, qual o valor do desvio
θ
após a luz voltar ao ar, sofrendo uma segunda refração
pela fase posterior do prisma? A situação é retratada na figura
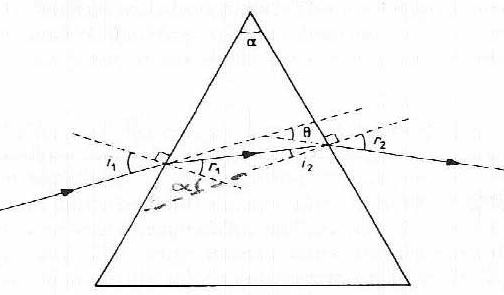
Se as faces anterior (de entrada da luz) e posterior (de saída da luz) do prisma formam um ângulo α entre si, e assumindo que o índice de refração do ar seja n1=1, o ângulo de desvio da luz em um comprimento de onda λ é dado por:
θ = i1+r2-α
onde i1 é o ângulo de incidência de entrada da luz e r2 é o ângulo de refração da luz na saída do prisma de volta para o ar, já que na figura podemos ver que:
θ=(i1-r1)+(i2-r2)
α = r1+r2
onde r1 é o ângulo de refração da luz ao entrar do ar para o prisma e i2 é o ângulo de incidência da luz sobre a face posterior do mesmo.
Podemos então escrever o desvio θ em função apenas de i1, n2 e de α, usando também a lei de Snell:
θ = i1-α+r2
θ = i1-α+arcsen[n2sen(i2)]
θ = i1-α+arcsen[n2sen(α-r1)]
θ = i1 - α + arcsen(n2 sen{α - arcsen[sen(i1)/n2]})
Note que i1 é o ângulo com que fazemos a luz incidir sobre o prisma, e n2 e α são propriedades do mesmo.
Com a expressão acima, podemos então determinar a dispersão dθ/dλ, usando dθ/dλ = (dθ/dn) (dn/dλ), onde n é índice de refração. O segundo termo, dn/dλ, é a dispersão do vidro, e é puramente uma propriedade do material.
A dispersão vai variar com o comprimento de onda, através da dependência de n2(λ). Podemos inclusive procurar determinar quais os valores de α e i1 que, para um determinado intervalo [λ1,λ2], maximizam a dispersão.
Johannes Franz Hartmann (1865-1936) escreveu a variação do índice de refração com o comprimento de onda como:
| Vidro | A | B | C |
|---|---|---|---|
| Crown | 1,477 | 3,20×10-8 | -2,10×10-7 |
| Flint | 1,603 | 2,08×10-8 | 1,43×10-7 |
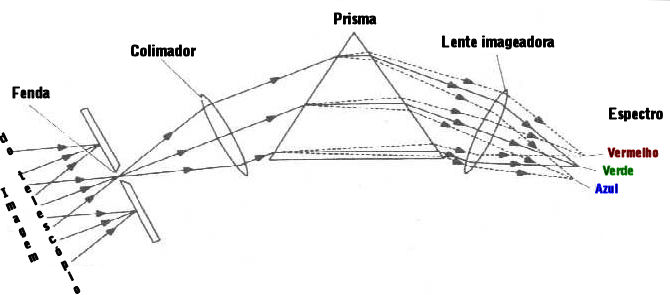
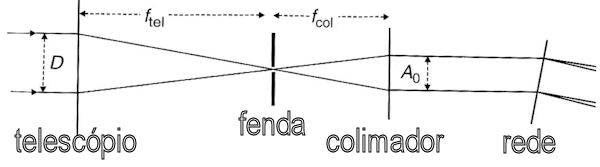
Podemos então pensar no espectro formado no plano do detector como sendo um conjunto infinito de imagens monocromáticas da fenda de entrada da luz e amplificadas pelo sistema óptico. A largura da imagem da fenda no detector, W, será
W = sf2/f1
onde f1 e f2 são, respectivamente, as distâncias focais do colimador e da lente imageadora e s é a largura da fenda.
A escala linear com que valores de λ são mapeados no detector ao longo da direção de dispersão x, é dada por
dλ/dx=(1/f2)(dλ/dθ)
É muito importante aqui estabelecer um paralelo com o imageamento. Sabemos que uma imagem em um detector mapeia pontos no céu em um espaço, geralmente um plano, do detector. Falamos então da escala do detector, dθ/dl que nos diz o ângulo no céu compreendido em um elemento de linha dl sobre o detector. No caso de um CCD, vimos que este elemento de linha é simplesmente o lado de um pixel do CCD. No caso de uma placa fotográfica, em geral dθ/dl mede-se em ″/mm.
A escala não deve ser confundida com a resolução da imagem, que é a capacidade de se resolver duas fontes próximas entre si. Na imagem, a escala é limitada pelo tamanho das células da atmosfera em observações ópticas baseadas em solo, que causam o seeing, ou pela abertura da superfície coletora de luz, para observações no limite de difração.
Em espectroscopia, a escala dλ/dx novamente apenas informa como se dá o mapeamento entre comprimento de onda e posição ao longo do espectro formado no detector. Mantendo a analogia com o imageamento puro e simples, podemos definir como resolução espectral a capacidade de se separar duas linhas próximas entre si (ou seja, com comprimentos de onda próximos) no espectro. Ou seja, qual a separação mínima dλ necessária para que as linhas estejam separadas no detector?
No caso ideal em que a imagem que alimenta o prisma seja limitada por difração, teremos que a imagem monocromática correspondente formada no detector será:
W = 1,22f2 λ/D
onde o termo 1,22λ/D é simplesmente o limite de difração de Rayleigh [John William Strutt, 3º Barão Rayleigh (1842-1919)]. Note-se que aqui D é a abertura do feixe colimado que incide sobre o elemento dispersor da luz, ou o tamanho do dispersor (rede), se menor, e não a abertura do telescópio. Essa abertura é sempre bem menor do que o diâmetro do primário do telescópio, o que significa que mesmo no caso de espectroscopia óptica, é possível e desejável alimentar o detector com uma imagem no limite de Rayleigh.
Rayleigh, em 1879 (Philosophical Magazine, 8, 261), deduziu que a distribuição de intensidades I(θ) do padrão de difração de uma abertura retangular de largura D é dada pela função seno cardeal ao quadrado, sinc2:
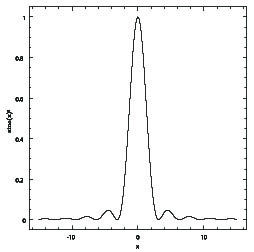
![$I(\theta) = [ \frac{{sen} ( \frac{\pi D {sen} \theta}{\lambda})}
{\frac{\pi D {sen} \theta}{\lambda}} ]^2 $](sinc.png)
Multiplicando a imagem limitada em difração, formada pela óptica do espectrógrafo, pela escala, teremos então a resolução espectral:
Δλ = W dλ/dx=W/f2 dλ/dθ = 1,22 λ/D dλ/dθ
Outra definição importante é o chamado poder resolutor R, dado pela razão entre o comprimento de onda e a resolução espectral:
R = λ/Δλ
Note que a escala espectral, dλ/dx, é expressa em unidades de Å/pixel (CCD) ou Å/mm (placa fotográfica). Já a resolução Δλ é usualmente expressa em Å, nm ou μm. O poder resolutor R é adimensional.Outro parâmetro fundamental de um espectrógrafo é a sua luminosidade, ou transmissão (throughput), definida como a fração dos fótons que chegam ao plano focal do telescópio e são registrados no detector. Parte dos fótons é perdida em reflexões, absorções, espalhamento e vinhetamento (vignetting - redução da intensidade nas bordas). Como a luz que atravessa um prisma sofre uma absorção, proporcional ao caminho atravessado pela luz, quanto maior é a resolução do prisma, proporcional à dimensão da base do prisma, maior é a perda por absorção. Esta é a razão que prismas não são competitivos com redes de difração, especialmente no azul, onde muitos vidros têm altos coeficientes de absorção. Por exemplo, Frank Lawton Olcott Wadsworth (1867-1936) publicou em 1903 (Philosophical Magazine, 5, 355) a descrição do espectrógrafo Bruce do Yerkes Observatory, com três prismas e base de 5,1 cm, com um coeficiente de absorção K3900Å=0,37. O espectrógrafo tem o nome da doadora dos recursos, Catherine Wolfe Bruce (1816-1900).
 A luz em uma direção θ é a interferência (soma) das componentes
de cada fenda. Em geral as fases das ondas de fendas diferentes são
distintas e se cancelam total ou parcialmente.
Quando a diferença de caminho entre as ondas de fendas adjacentes é
igual ao comprimento de onda, λ, as ondas estão em fase.
Isto ocorre para ângulos θmáximo que satisfazem
a relação
dsen(θmáximo)=|n|λ,
onde d é a separação entre as fendas
e n é um inteiro. Portanto os máximos da luz difratada ocorrem
A luz em uma direção θ é a interferência (soma) das componentes
de cada fenda. Em geral as fases das ondas de fendas diferentes são
distintas e se cancelam total ou parcialmente.
Quando a diferença de caminho entre as ondas de fendas adjacentes é
igual ao comprimento de onda, λ, as ondas estão em fase.
Isto ocorre para ângulos θmáximo que satisfazem
a relação
dsen(θmáximo)=|n|λ,
onde d é a separação entre as fendas
e n é um inteiro. Portanto os máximos da luz difratada ocorrem
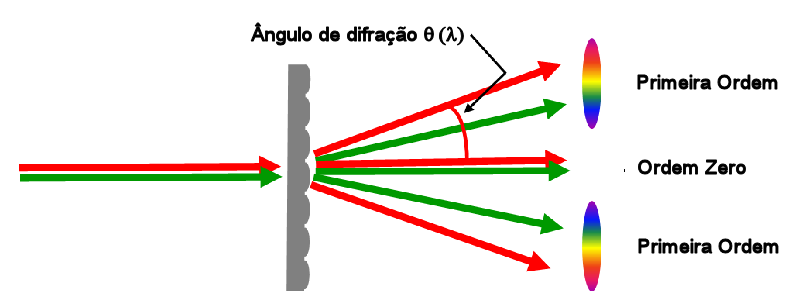
A luz que corresponde à transmissão direta (ou reflexão especular se a rede for de reflexão) é chamada de ordem zero, correspondente a n=0. Outros máximos ocorrem em ângulos representados por n diferentes de zero, que podem ser positivos ou negativos, dependendo da direção em relação ao feixe de ordem zero.
![$I(\theta) = 2I_0[
\frac{{sen} ( \frac{\pi D\, \theta... ...c{\pi D\, \theta}{\lambda}}
\Biggr]^2 [1+\cos(2\pi\Delta/\lambda+2\pi d \theta)/\lambda]$](fr.png)
 Animação de
physics-animation.com mostrando o efeito de aumentar a largura de uma fenda única.
Animação de
physics-animation.com mostrando o efeito de aumentar a largura de uma fenda única.
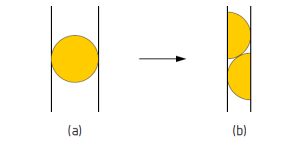
 Animação
mostrando o efeito de aumentar o tamanho de duas fendas,
enquanto a separação entre elas é mantida constante.
Animação
mostrando o efeito de aumentar o tamanho de duas fendas,
enquanto a separação entre elas é mantida constante.
 Animação
mostrando o efeito de aumentar a separação de duas fendas,
enquanto a largura é mantida constante.
Animação
mostrando o efeito de aumentar a separação de duas fendas,
enquanto a largura é mantida constante.
Embora nossa discussão esteja baseada em fendas, se substituirmos
as fendas por pequenos espelhos, os resultados não são alterados.
Desde modo, as redes podem ser de transmissão ou de reflexão. A
maioria dos espectrógrafos astronômicos são feitos com redes
de reflexão.

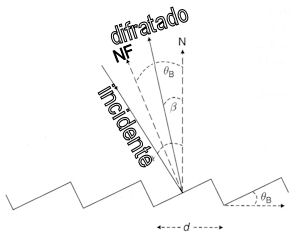 A maioria das redes usadas é de reflexão e inclinando-se o feixe incidente
para que a reflexão seja especular, isto é, na mesma direção do feixe
incidente, aumenta-se a eficiência. Portanto o blazing
da rede é mudar o ângulo das facetas para coincidir com a ordem
que se quer observar, isto é, concentrando a luz em um ângulo sólido
pequeno. Na figura θB é o ângulo de blazing,
N a normal à base da rede e NF a normal à faceta da rede.
A maioria das redes usadas é de reflexão e inclinando-se o feixe incidente
para que a reflexão seja especular, isto é, na mesma direção do feixe
incidente, aumenta-se a eficiência. Portanto o blazing
da rede é mudar o ângulo das facetas para coincidir com a ordem
que se quer observar, isto é, concentrando a luz em um ângulo sólido
pequeno. Na figura θB é o ângulo de blazing,
N a normal à base da rede e NF a normal à faceta da rede.
 [Sir George Biddell Airy (1801-1892)],
produzido pelo telescópio de abertura D.
[Sir George Biddell Airy (1801-1892)],
produzido pelo telescópio de abertura D.
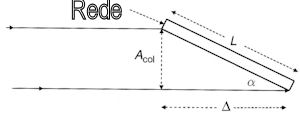 A equação do poder de resolução no
limite de difração é uma conseqüência
direta do princípio da incerteza de Heisenberg, ΔxΔp=h.
A incerteza na posição do fóton
difratado por uma rede de difração de reflexão
é Δx = 2Δ = 2L senθB.
A incerteza no momentum Δp=Δ(h/λ)=(h/λ2)Δλ.
Logo ΔxΔp=[(2hL senθB)/λ2]Δλ=h,
que se torna
λ/(Δλ) = 2L senθB/λ, e
A equação do poder de resolução no
limite de difração é uma conseqüência
direta do princípio da incerteza de Heisenberg, ΔxΔp=h.
A incerteza na posição do fóton
difratado por uma rede de difração de reflexão
é Δx = 2Δ = 2L senθB.
A incerteza no momentum Δp=Δ(h/λ)=(h/λ2)Δλ.
Logo ΔxΔp=[(2hL senθB)/λ2]Δλ=h,
que se torna
λ/(Δλ) = 2L senθB/λ, e
Estas expressões para o poder de resolução ressaltam que um alta resolução depende de:
Arthur Schuster (1851-1934) em seu artigo de 1884 na Enciclopédia Britânica, 9ª edição, 22, 373, demonstrou que a resolução total é a combinação da resolução por difração com a resolução limitada pela fenda,
Como escolher a largura da fenda? Para obter a melhor resolução possível no espectro, use a fenda do tamanho do limite de difração. Mas isto certamente ocasionará perda de luz nas bordas da fenda, de modo que se o objeto for fraco ou se estiver interessado em espectrofotometria, utilize a fenda maior, que inclua toda a luz da estrela, cerca de 2 vezes o tamanho da imagem (disco de seeing) pelo menos. Isto levará à resolução limitada pela fenda, mas incluirá a maior parte da luz no espectro.
A resolução necessária depende da ciência: 500 pode ser suficiente para uma procura de objetos com linhas de emissão, 1000 para medir os redshifts de quasares distantes, 2500 para classificação espectral de estrelas, 10 mil para medir o perfil da linha de estrelas, 25 mil para análise de abundâncias químicas, e 100 mil quando linhas interestelares, com seus múltiplos componentes, precisam ser resolvidas.
Em geral considera-se que as nuvens são cinza, isto é, que a extinção causada por nuvens não afeta a forma do espectro, somente sua intensidade. Desta forma pode-se obter espectroscopia mesmo com nuvens, mas não espectrofotometria. A espectrofotometria necessita que toda a luz seja observada, pois o fluxo pode ser usado para determinar o ângulo sólido da estrela, já que fluxo é proporcional a R2/d2, onde R é o raio do objeto e d sua distância. Naturalmente para se obter o fluxo real da estrela é necessário medir estrelas de calibração espectrofotométricas em várias massas de ar, para determinar a extinção e a sensibilidade do instrumento em cada comprimento de onda. Mesmo quando só estamos interessados nas razões de linha, é necessário calibrar por fluxo, para que as variações do contínuo ao longo da linha não introduzam incertezas. As estrelas padrões espectrofotométricas em geral são calibradas em caixas de 50 Å ou 16 Å. Quanto menor o tamanho da caixa, melhor. Quatro anãs brancas quentes, G 191-B2B, GD 153 e GD 71 e HZ 43, as padrões espectrofotométricas primárias do Telescópio Espacial Hubble, estão calibradas em caixas de 1 Å. Se possível, observe estas padrões para poder aplicar uma correção fina ao espectro final, normalizando o espectro observado da padrão com o seu espectro dela, observado com o mesmo instrumento, mesma rede e mesmo ângulo de incidência.
Padrões Espectrofotométricas Primárias do HST
Estrela AR (J2000) Dec B-V V Tipo Tef log g
h m s g ′ ″ (K)
-------------------------------------------------------------------
G191-B2B 05 05 30.6 +52 49 54 -0.326 11.781 DA0 61300 7.50
GD 71 05 52 27.5 +15 53 17 -0.249 13.032 DA1 32300 7.73
GD 153 12 57 02.4 +22 01 56 -0.286 13.346 DA1 38500 7.67
HZ 43 13 16 22.0 +29 05 57 -0.302 12.914 DA1 50000 8.00

O espectrógrafo HARPS (High Accuracy Radial-Velocity Planet Searcher), instalado no telescópio de 3,6 m New Technology Telescope do ESO, alcança precisão de 0,9 m/s. Ele usa uma grande rede échelle R4 (837×208 mm), com dispersão cruzada por um grisma FK5, atingindo uma resolução de 115 mil. Uma exposição de Th-Ar é registrada junto ao espectro estelar. Todo o espectrógrafo está instalado dentro de um grande tanque de vácuo.
Para manter a resolução da rede, é necessário que o detector tenha pelo menos dois píxeis por elemento de resolução, de acordo com o teorema de Nyquist [Harry Nyquist (1889-1976), Transactions of the American Institute of Electral Engineers, 47, 617, 1928]. Outra preocupação é com o ruído de leitura, já que a contagem em cada píxel de um espectro é baixa para objetos fracos, além do número total de píxeis necessários para observar todo o espectro, mantendo a resolução.
Já a capacidade de se separar duas linhas em um espectro é dada pela resolução espectral.
Se uma linha é bem resolvida em um espectro, ou seja, não tem outras linhas a ela superpostas, então podemos tentar medir o fluxo dessa linha, dado pela expressão
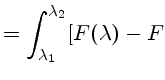 contínuo
contínuoOu seja, o fluxo da linha é uma medida da área em excesso ou em falta, com relação ao contínuo, correspondente àquela linha. Por essa definição, se a linha for de emissão, como no espectro de uma nebulosa ou disco de acresção, por exemplo de um núcleo ativo de galáxia, F(λ)>Fcontínuo, de forma que Flinha>0. Se a linha for de absorção, como tipicamente se encontra em espectros estelares, teremos F(λ)<Fcontínuo, de forma que Flinha<0. Podemos inverter a ordem dos termos no integrando do fluxo de linha, de forma a fazê-lo sempre positivo.
Uma definição semelhante, que mede o fluxo de uma linha, é a chamada largura equivalente, W ou EW. Ela é dada pela expressão
![$W = \int_{\lambda_1}^{\lambda_2} {\frac{[F(\lambda)-F_{\mbox{contínuo}}]}
{F_{\mbox{contínuo}}}}
d\lambda$](W.png)
Notem que
W contem essencialmente a mesma informação que o fluxo da linha. A
diferença é que F(λ) é medido
em unidades de fluxo (como W/m2,
por exemplo).
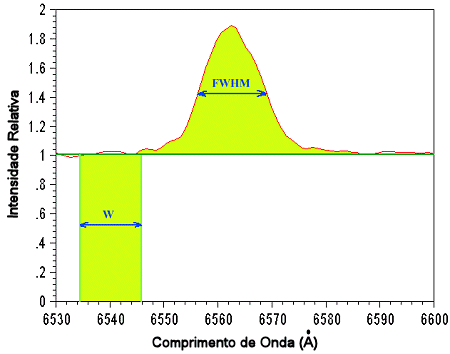
A interpretação
da largura equivalente é a largura
que uma linha de forma retangular teria, contendo o mesmo fluxo que a linha
que se está medindo. Vale notar também que a inversão da ordem
dos termos do integrando na definição de W agora faz com que
W>0 no caso de linhas de absorção e W<0 para linhas de emissão.
Mas reiteramos que o sinal pode ser modificado por uma
simples inversão da subtração no integrando, de forma que
o sinal não é muito relevante nessas medidas.
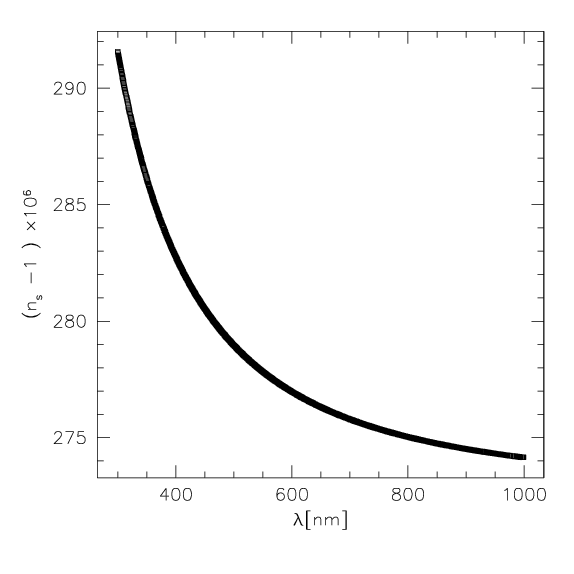 O índice de refração do ar, mostrado na figura, depende do comprimento
de onda, de modo que cada ponto do objeto aparece como um
pequeno espectro, perpendicular ao horizonte.
O índice de refração do ar, mostrado na figura, depende do comprimento
de onda, de modo que cada ponto do objeto aparece como um
pequeno espectro, perpendicular ao horizonte.
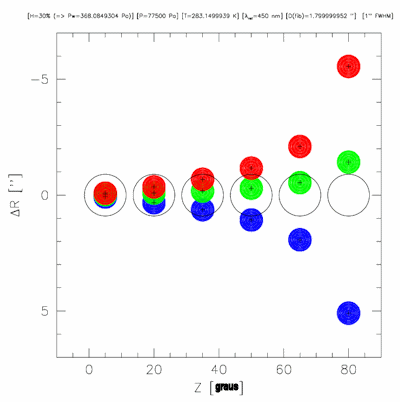
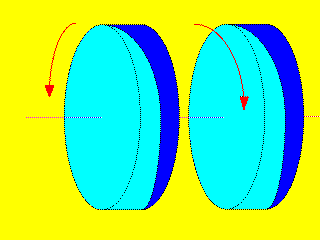 Usando-se dois primas acimentados juntos, com mesmo ângulo mas índices
de refração diferentes, obtem-se
um dubleto de faces planas. A luz de comprimento de onda intermediário passa
sem desvio, enquanto a luz de comprimentos de ondas curtos e longos
são desviados para compensar a dispersão atmosférica.
Para permitir o ADC de compensar em massas de ar distintas, a correção
é feita em dois destes dubletos, cada um produzindo metade da correção.
Os dois dubletos precisam girar independemente, de modo que quando estão
em orientações opostas eles produzem dispersão nula, enquanto
a máxima dispersão ocorre quando estão alinhados.
Usando-se dois primas acimentados juntos, com mesmo ângulo mas índices
de refração diferentes, obtem-se
um dubleto de faces planas. A luz de comprimento de onda intermediário passa
sem desvio, enquanto a luz de comprimentos de ondas curtos e longos
são desviados para compensar a dispersão atmosférica.
Para permitir o ADC de compensar em massas de ar distintas, a correção
é feita em dois destes dubletos, cada um produzindo metade da correção.
Os dois dubletos precisam girar independemente, de modo que quando estão
em orientações opostas eles produzem dispersão nula, enquanto
a máxima dispersão ocorre quando estão alinhados.
Mesmo usando filme antireflexivo em todas as superfícies, as perdas de luz das melhores ADC são da ordem de 10%, por causa da absorção do vidro e perdas por reflexão nas 4 superfícies. Se não houver correção, a perda pode chegar a 100%, se a imagem no comprimento de onda de interesse não estiver na fenda, ou se estamos guiando o telescópio com uma estrela de cor muito diferente do objeto.
No SOAR, a ADC do SOI ainda não entá em operação. No Gemini, a ADC do GMOS
também não está operacional. O ADC do Goodman está nominalmente em operações.
A redução de dados de espectroscopia começa com a redução das imagens CCDs normais: overscan, bias, flat, mas com um cuidado extra na normalização do flatfield, já que a iluminação das lâmpadas ou céu não é nada homogênea com o comprimento de onda. A tarefa do IRAF noao.twodspec.longslit.response é utilizada para determinar a sensibilidade do detector à lâmpada, para a normalização. Para a observação de objetos extensos também há problemas com a iluminação desigual da lâmpada, se flat de lâmpada, e existe a tarefa noao.twodspec.longslit.illumination para corrigir o flat, se houve medidas de flat de céu (skyflats).
 Espectro da estrela padrão HR 5501.
Espectro da estrela padrão HR 5501.
Primeiro é preciso informar a direção de dispersão na imagem. Para o Soar, NOAO e Gemini, a direção é 2 e para o ESO é 1. Isto é feito com epar apextract:
dispaxis,i,h,1,1,2,"Dispersion axis (1=along lines, 2=along columns)"
Para definir a forma da fenda, é recomendável utilizar-se uma imagem com boa exposição em todos os comprimentos de onda, por exemplo da estrela padrão. Deve-se utilizar um polinômio de baixa ordem para a fitagem da forma e, de preferência, funções polinomiais como Legendre [Adrien-Marie Legendre (1752-1833)] ou Chebyshev [Pafnuty Lvvich Chebyshev (1821-1894)], e não splines, que podem divergir nas bordas.
 Espectro de uma estrela anã branca
Espectro de uma estrela anã branca
Defina a abertura que inclui toda a luz da estrela: tecle n com o cursor no centro da abertura, ou m para que o IRAF calcule o centróide. d apaga a abertura. l define a borda inferior (lower) no ponto do mouse, e u define a borda superior (upper). Para definir a região de céu (background), tecle b. As barras mostradas mostram as regiões usadas. Tecle s para setar novas regiões, teclando s nas extremidades da região próxima à abertura onde queres medir o céu. Tecle f para fitar e a linha pontilhada mostra o valor fitado. z apaga as regiões selecionadas. Tecle q para voltar para a janela de definição de abertura, e q para sair do modo de definição da abertura. O gráfico mostra agora a abertura fitada ao longo do espectro, com + para os dados e a linha pontilhada para o ajuste. Atente que o eixo y- em geral mostra somente poucos píxeis. Para mudar a ordem do ajuste para um polinômio de 4a ordem, por exemplo, tecle :or 4 (não se esqueça dos :). Tecle f para fitar. Não use polinômios mais altos. Apague os pontos muito fora da curva, teclando d e fitando novamente com f. Tecle q para sair da janela da fitagem da abertura. Responda às perguntas para extrair e plotar o espectro.
Quando for definir a abertura de uma estrela fraca, lembre-se que a forma da fenda não muda e, portanto, se a função fitada divergir nas bordas por ausência de sinal, force a forma de forma a ficar parecida com a da estrela brilhante. Voce pode usar trace- recenter+ para usar a forma da fenda obtida em uma fitagem anterior, por exemplo da estrela padrão, recentrada no espectro atual, mas a refração atmosférica pode alterar levemente a forma, especialmente se a fenda não está orientada no ângulo paralático, isto é, perpendicular ao horizonte.

Ao extrair o espectro dos objetos, faz-se a subtração do céu,
escolhendo-se uma região afastada da estrela.
 Espectro da Lâmpada de HgAr
Espectro da Lâmpada de HgAr
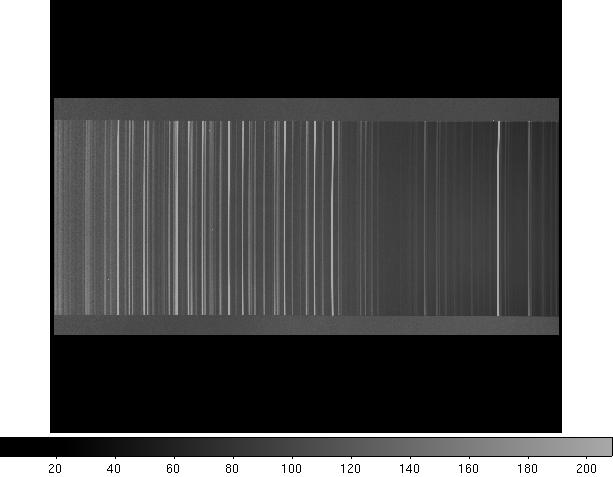 Espectro da Lâmpada de Cobre
Espectro da Lâmpada de Cobre
Após extrair os espectros dos objetos, extraia o espectro da
lâmpada correspondente, obtida com o telescópio na mesma posição
do objeto para que não haja mudança de flexão no espectrógrafo,
e utilizando a fenda definida pela estrela.
Execute o apall sem fitar a fenda (trace- recenter-),
e sem a subtração do céu, no caso das lâmpadas,
já que há exposição da lâmpada em toda a imagem (background-).
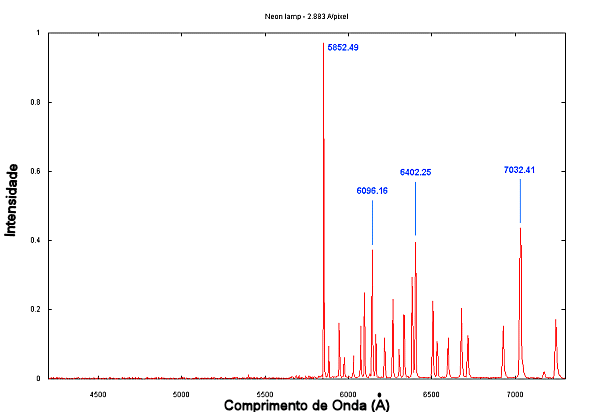
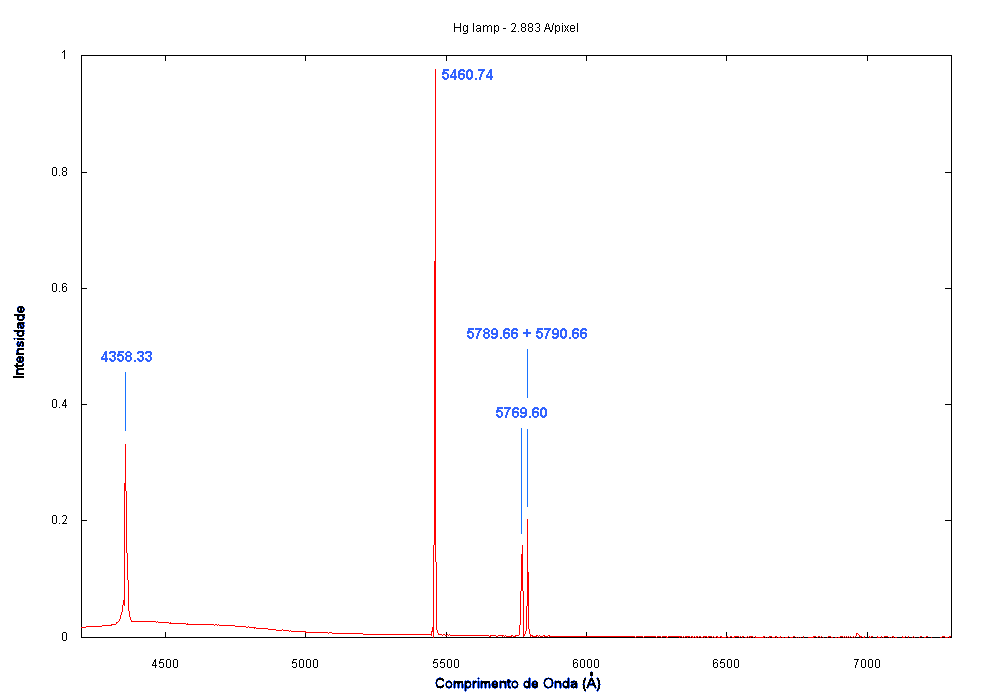 É necessário também ter um arquivo com a tabela das linhas existentes
para a lâmpada, por exemplo, CuHgHeAr.dat. Cuide para que
o arquivo só tenha linhas dos elementos da lâmpada, ou seja muito cuidadoso em só utilizar linhas
dos elementos da lâmpada.
Após marcar algumas linhas, principalmente as linhas mais fortes
próximas das bordas do detector, com
o comando m, use o comando f para
que o IRAF ajuste (fit) um polinômio, novamente
de preferência funções polinomiais como Legendre ou
Chebyshev, e não splines, de baixa ordem.
O comando r mostra os resíduos.
Lembre-se que ? lista os comandos. Veja se há alguma linha muito
discrepante na fitagem e apague-a, se necessário. O comando q
sai da fitagem e volta ao gráfico das linhas, onde o comando
:labels coord mostra os comprimentos de onda das linhas identificadas.
O comando l fita automaticamente as próximas linhas,
usando o polinômio fitado, e use o comando f para
uma nova fitagem, usando as novas linhas identificadas,
o comando r mostra os resíduos. Veja se há alguma linha muito
discrepante na fitagem e apague-a, se necessário.
No gráfico das linhas, pode-se expandir o gráfico e estimar a largura
de cada linha da lâmpada, o que nos dá uma medida da resolução do
espectro e uma idéia do valor aceitável para o resíduo de cada linha.
Entre z seguido de múltiplos + para examinar cada linha.
Quando estiver satisfeito com as linhas identificadas, entre q
para sair do identify.
É necessário também ter um arquivo com a tabela das linhas existentes
para a lâmpada, por exemplo, CuHgHeAr.dat. Cuide para que
o arquivo só tenha linhas dos elementos da lâmpada, ou seja muito cuidadoso em só utilizar linhas
dos elementos da lâmpada.
Após marcar algumas linhas, principalmente as linhas mais fortes
próximas das bordas do detector, com
o comando m, use o comando f para
que o IRAF ajuste (fit) um polinômio, novamente
de preferência funções polinomiais como Legendre ou
Chebyshev, e não splines, de baixa ordem.
O comando r mostra os resíduos.
Lembre-se que ? lista os comandos. Veja se há alguma linha muito
discrepante na fitagem e apague-a, se necessário. O comando q
sai da fitagem e volta ao gráfico das linhas, onde o comando
:labels coord mostra os comprimentos de onda das linhas identificadas.
O comando l fita automaticamente as próximas linhas,
usando o polinômio fitado, e use o comando f para
uma nova fitagem, usando as novas linhas identificadas,
o comando r mostra os resíduos. Veja se há alguma linha muito
discrepante na fitagem e apague-a, se necessário.
No gráfico das linhas, pode-se expandir o gráfico e estimar a largura
de cada linha da lâmpada, o que nos dá uma medida da resolução do
espectro e uma idéia do valor aceitável para o resíduo de cada linha.
Entre z seguido de múltiplos + para examinar cada linha.
Quando estiver satisfeito com as linhas identificadas, entre q
para sair do identify.

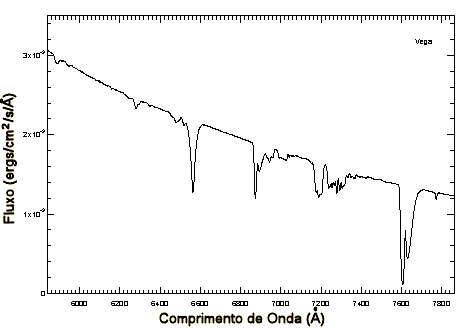 Utilize a tarefa standard e
sensfunc nas medidas de estrela padrão
para calcular a sensibilidade do espectrógrafo, e em seguida
calibre o espectro do objeto com esta curva de sensibilidade,
usando calibrate,
corrigindo também por massa de ar. Somente após estas correções
é possível somar os espectros do mesmo objeto, utilizando por
exemplo a tarefa scombine. Se houver mais de dois espectros
do mesmo objeto, é possível fazer a rejeição dos píxeis discrepantes,
por exemplo com o avsigclip.
Utilize a tarefa standard e
sensfunc nas medidas de estrela padrão
para calcular a sensibilidade do espectrógrafo, e em seguida
calibre o espectro do objeto com esta curva de sensibilidade,
usando calibrate,
corrigindo também por massa de ar. Somente após estas correções
é possível somar os espectros do mesmo objeto, utilizando por
exemplo a tarefa scombine. Se houver mais de dois espectros
do mesmo objeto, é possível fazer a rejeição dos píxeis discrepantes,
por exemplo com o avsigclip.
Cada tarefa do IRAF escreve uma linha no logfile, e o splot no splot.log. Algumas tarefas, como o noao.imred.ccdred sobre-escrevem as imagens iniciais, se nenhum nome de saída (output) for dado. Outras, como o mscred.ccdproc criam um backup (bkuproot=Raw/ por default) com as imagens originais. Algumas tarefas escrevem seus parâmetros e resultados dos ajustes no diretório database/.
O manual de introdução ao IRAF é o primeiro passo.
Os
tutoriais do IRAF
em espectroscopia de fenda longa estão em
http://iraf.noao.edu/iraf/web/tutorials/doslit/doslit.html,
http://www.twilightlandscapes.com/IRAFtutorial/IRAFintro_06.html.
Espectroscopia de Campo Integral (IFUS)
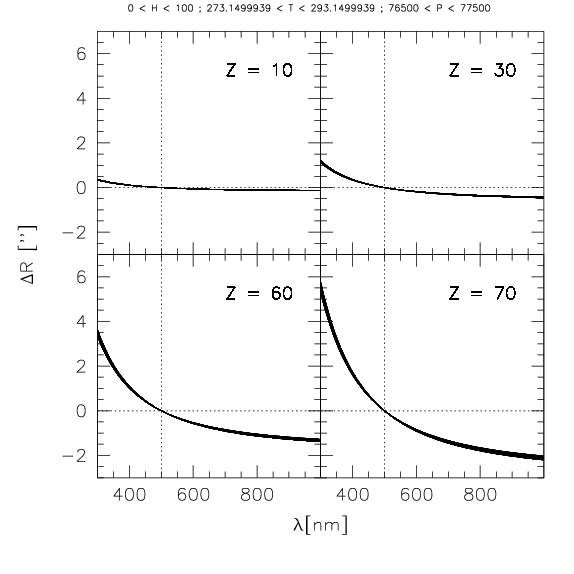
Como a refração atmosférica depende do comprimento de onda, a imagem de cada ponto em comprimentos
de onda diferentes aparece em posições diferentes no plano focal do telescópio. Se o instrumento
não dispõe de um bom ADC (corretor de dispersão atmosférica),
é preciso corrigir por isto:
É crucial escolher uma padrão espectrofotométrica que não seja variável. A padrão
LTT 4816=BPM 37093, é uma anã branca pulsante, embora de baixa
amplitude. As linhas vermelhas, no gráfico abaixo, mostram linhas fortes do céu, incluindo as linhas de O2 A e B de Fraunhofer, que muitas vezes contaminam o espectro resultante porque não são completamente subtraídas com o céu. Nestes espectros, somente as linhas
de H, como as marcadas em preto, são da estrela.
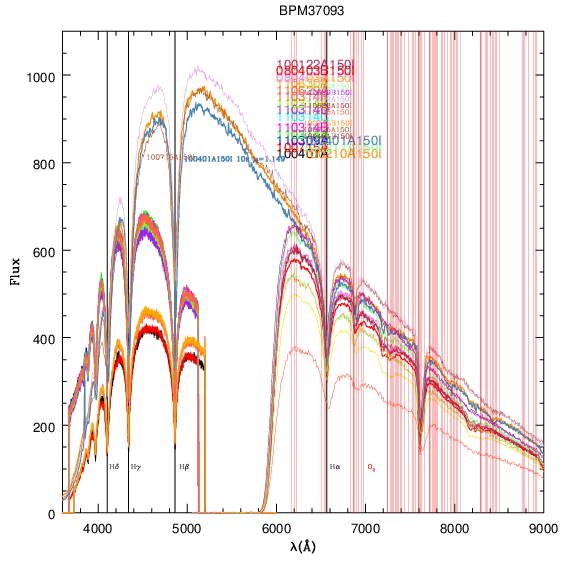
Para reduzir espectros do ESO, pode-se usar o Reflex, que administra as receitas em Python, e gera os espectros extraídos e, se houverem dados de estrelas padrõoes no intervalo de até sete dias das observações, calibra em fluxo. Para o macOS, recomenda-se a instalação pelo MacPorts.
Por exemplo, para reduzir espectros do
FORS,
use
a receita
e o tutorial.
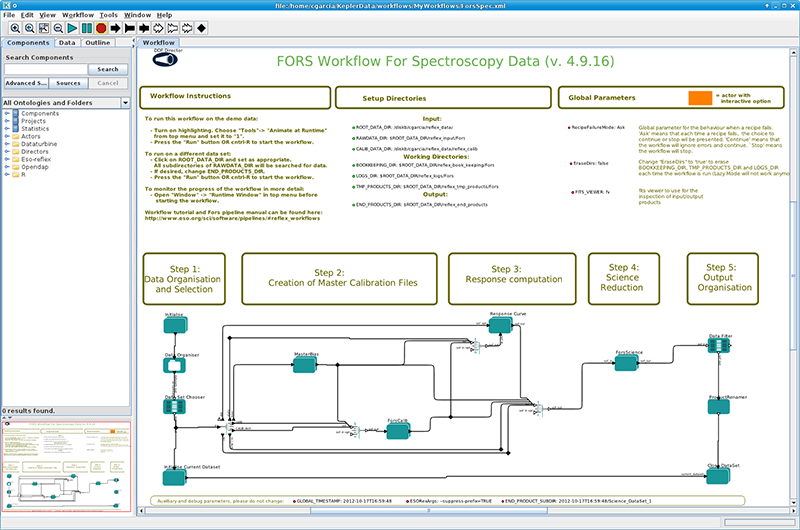
Linhas do céu com o UVES
Em outubro de 2011 os CCDs do GMOS-N foram
substituídos por deep depletion e2v e
novas curvas de calibração foram
obtidas.
Em setembro de 2015 os
CCDs e2V foram substituidos por Hamamatsu, com maior eficiência entre 5500 e 10 000 Å,
primeiro no sul e depois no norte, porém com outras instabilidades ainda presentes, e que mudam quando há ciclos de temperatura no instrumento.
Espectro da Anã Marrom Gliese 570 D e suas linhas moleculares.
Espectrógrafo clássico (em inglês)
Abaixo de 3200Å, a absorção do ozônio atmosférico aumenta rapidamente,
de modo que observações de espectros entre 2000 e 3000Å requerem observações
em altitudes de no mínimo 40 a 50 km. Entre 1000 e 2000Å o absorção
por oxigênio molecular (O2) torna-se ainda mais opaca que a do ozônio,
e as observações requerem no mínimo 100 km de altura. Abaixo de 912Å,
a absorção pelo hidrogênio neutro interestelar torna o meio interestelar opaco
[Sir Robert Wilson (1927-2002)
& Alexander Boksenberg (1936-), 1969, Ultraviolet Astronomy, Annual Review of Astronomy and Astrophysics, 7, 421].
SOAR - Goodman Spectrograph Data Reduction Pipeline
Silicon Immersion Grating
Planejando um espectrógrafo com CD (em inglês)
![]() Telescópios e Instrumentos
Telescópios e Instrumentos
![]() Astronomia e Astrofísica
Astronomia e Astrofísica
![]()
Modificada em 11 jun 2018