


| Tycho | Kepler | Elipses | Galileo |
A Teoria Heliocêntrica conseguiu dar explicações mais simples e naturais para os fenômenos observados (por exemplo, o movimento retrógrado dos planetas), porém Copérnico não conseguiu prever as posições dos planetas de forma precisa, assumindo que as órbitas eram circulares, nem conseguiu provar que a Terra estava em movimento.



Três anos após a morte de Copérnico, nasceu o dinamarquês Tycho Brahe (1546-1601), o último grande astrônomo observacional antes da invenção do telescópio. Usando instrumentos fabricados por ele mesmo, Tycho fez extensivas observações das posições de planetas e estrelas, com uma precisão em muitos casos melhor do que 1 minuto de arco (1/30 do diâmetro aparente do Sol). No seu livro Astronomia instauratae mechanica, de 1598, ele descreve como desenvolveu e utilisou quatro tipos diferentes de esferas armilares, melhores do que as de Hiparcos e as de Ptolomeu, descritas no Syntaxis de Ptolomeu. Tycho podia medir diretamente as coordenadas eclípticas ou equatorias dos objetos celestes, com as esferas, enquanto seus outros instrumentos mediam coordenadas horizontais (altura e azimute). Sua maior esfera armilar tinha 2,6 metros de diâmetro, e ele descreveu que a maior fonte de erro era a flexão e deslocamento dos círculos (armillae, em latim), devido ao seu próprio peso.
O excelente trabalho de Tycho como observador lhe propiciou o patrocínio do rei da Dinamarca, Frederic II (1534-1588), e assim Tycho pode construiu seu próprio observatório, na pequena ilha báltica de Hven (entre Dinamarca e Suécia).

Após a morte do rei, entretanto, seu sucessor se desentendeu com Tycho e retirou seus privilégios. Assim, em 1597 Tycho foi forçado a deixar a Dinamarca, e foi trabalhar como astrônomo da corte para o imperador da Bohemia, em Praga.
Tycho Brahe não acreditava na hipótese heliocêntrica de Copérnico, mas foram suas observações dos planetas que levaram às leis de Kepler do movimento planetário.
Em 1600 (um ano antes de sua morte), Tycho contratou para ajudá-lo na análise dos dados sobre os planetas, colhidos durante 20 anos, um jovem e hábil matemático alemão chamado Johannes Kepler (1571-1630).

Quando Tycho morreu, Kepler "herdou" seu posto e seus dados, a cujo estudo se dedicou pelos 20 anos seguintes.
O planeta para o qual havia o maior número de dados era Marte. Kepler conseguiu determinar as diferentes posições da Terra após cada período sideral de Marte, e assim conseguiu traçar a órbita da Terra. Encontrou que essa órbita era muito bem ajustada por um círculo excêntrico, isto é, com o Sol um pouco afastado do centro.

Kepler conseguiu também determinar a órbita de Marte, mas ao tentar ajustá-la com um círculo não teve sucesso. Ele continuou insistindo nessa tentativa por vários anos, e em certo ponto encontrou uma órbita circular que concordava com as observações com um erro de 8 minutos de arco. Mas sabendo que as observações de Tycho não poderiam ter um erro desse tamanho (apesar disso significar um erro de apenas 1/4 do tamanho do Sol), Kepler descartou essa possibilidade.
Finalmente, passou à tentativa de representar a órbita de Marte com uma oval, e rapidamente descobriu que uma elipse ajustava muito bem os dados. [O indiano Aryabhata I (476-550), escreveu em seu tratado de astronomia e matemática, Aryabhatiya, que as órbitas dos planetas em torno do Sol deveriam ser elipses]. A posição do Sol coincidia com um dos focos da elipse. Ficou assim explicada também a trajetória quase circular da Terra, com o Sol afastado do centro.


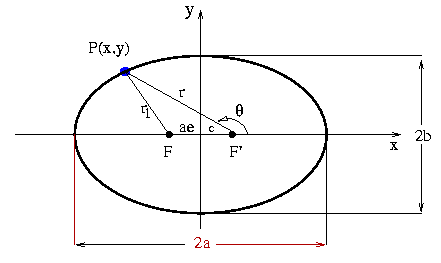
![]()
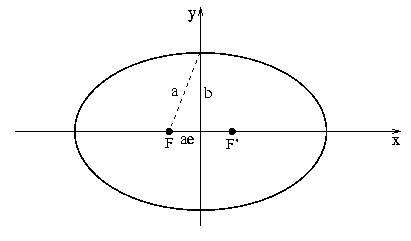
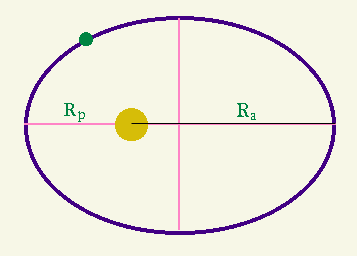
 A órbita de cada planeta é uma elipse, com o Sol em um dos focos.
Como consequência da órbita ser elíptica, a distância do Sol
ao planeta varia ao longo de sua órbita.
A órbita de cada planeta é uma elipse, com o Sol em um dos focos.
Como consequência da órbita ser elíptica, a distância do Sol
ao planeta varia ao longo de sua órbita.
Sendo P o período sideral do planeta, a o semi-eixo maior da órbita, que é igual à distância média do planeta ao Sol, e K uma constante, podemos expressar a 3a lei para os planetas do Sistema Solar como:
![]()
Se medimos P em anos (o período sideral da Terra), e a em unidades astronômicas (a distância média da Terra ao Sol), então K = 1, e podemos escrever a 3a lei como:
![]()
A tabela abaixo mostra como fica a ![]() Lei de Kepler para os planetas
visíveis a olho nu.
Lei de Kepler para os planetas
visíveis a olho nu.
| Planeta | Semi-eixo | Período | ||
|---|---|---|---|---|
| Maior (UA) | (anos) | a3 | P2 | |
| Mercúrio | 0,387 | 0,241 | 0,058 | 0,058 |
| Vênus | 0,723 | 0,615 | 0,378 | 0,378 |
| Terra | 1,000 | 1,000 | 1,000 | 1,000 |
| Marte | 1,524 | 1,881 | 3,537 | 3,537 |
| Júpiter | 5,203 | 11,862 | 140,8 | 140,7 |
| Saturno | 9,534 | 29,456 | 867,9 | 867,7 |

Galileo começou suas observações telescópicas em 1609, usando um telescópio construído por ele mesmo. Não cabe a Galileo o crédito da invenção do telescópio, no entanto. Lentes e óculos já eram conhecidos desde cerca de 1350, e Galileo tinha ouvido falar do telescópio construído pelo holandês Hans Lippershey (1570-1619) em 1608. Galileo soube desse instrumento em 1609, e, sem ter visto o telescópio de Lippershey, construiu o seu próprio, com aumento de 3 vezes, ainda em 1609. Em seguida ele construiu outros instrumentos, e o melhor tinha aumento de 30 vezes.
Galileo usou o telescópio para observar sistematicamente o céu, fazendo várias descobertas importantes, como:
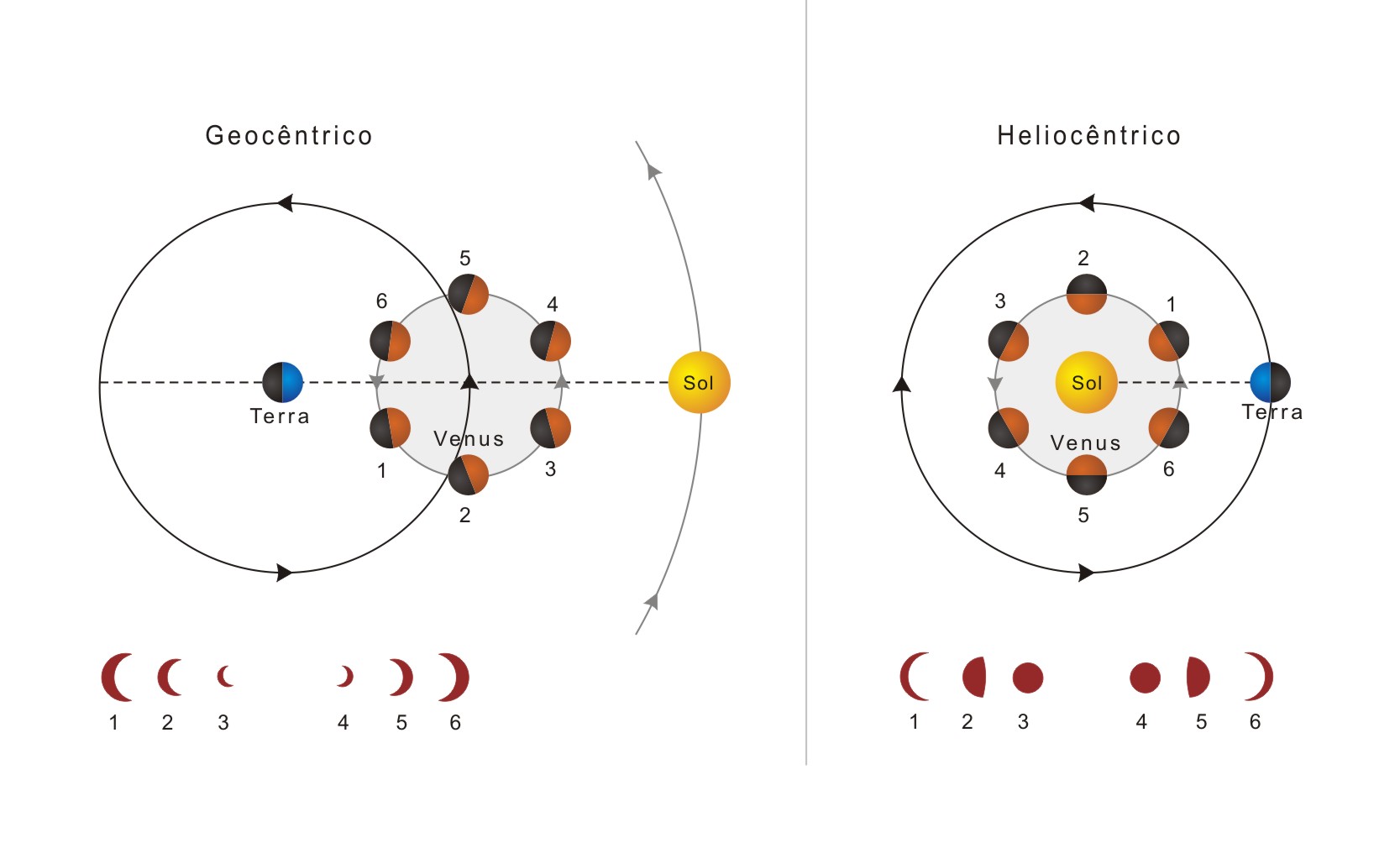
 Essa descoberta também foi fundamental porque, no sistema ptolomaico, Vênus
está sempre mais próximo da Terra do que o Sol, e como Vênus está
sempre próximo do Sol, ele nunca poderia ter toda sua face
iluminada voltada para nós (fase cheia) e,
portanto, deveria sempre aparecer como nova ou no máximo
crescente. Ao ver que Vênus muitas vezes aparece em fase quase
totalmente cheia, Galileo concluiu que ele viaja ao redor do Sol,
passando às vezes pela frente dele
e outras vezes por trás dele,
e não revolve em torno da Terra.
Essa descoberta também foi fundamental porque, no sistema ptolomaico, Vênus
está sempre mais próximo da Terra do que o Sol, e como Vênus está
sempre próximo do Sol, ele nunca poderia ter toda sua face
iluminada voltada para nós (fase cheia) e,
portanto, deveria sempre aparecer como nova ou no máximo
crescente. Ao ver que Vênus muitas vezes aparece em fase quase
totalmente cheia, Galileo concluiu que ele viaja ao redor do Sol,
passando às vezes pela frente dele
e outras vezes por trás dele,
e não revolve em torno da Terra.
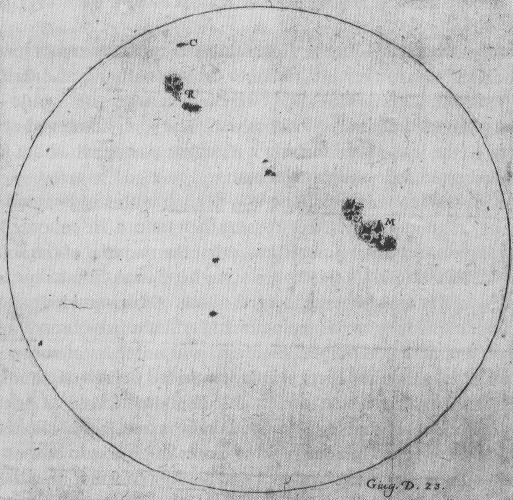
 As descobertas de Galileo proporcionaram grande quantidade de evidências em
suporte ao sistema heliocêntrico. Por causa disso, ele foi
chamado a depor ante a Inquisição Romana, sob acusação de
heresia, e
obrigado a se retratar.
Apenas em 1980, o Papa João Paulo II
[Karol Joseph Wojtyla (1920-2005)]
ordenou um re-exame do processo contra
Galileo, o que acabou por eliminar os últimos vestígios de
resistência, por parte da igreja Católica, à revolução Copernicana.
Galileo foi perdoado em 31 de outubro de 1992.
As descobertas de Galileo proporcionaram grande quantidade de evidências em
suporte ao sistema heliocêntrico. Por causa disso, ele foi
chamado a depor ante a Inquisição Romana, sob acusação de
heresia, e
obrigado a se retratar.
Apenas em 1980, o Papa João Paulo II
[Karol Joseph Wojtyla (1920-2005)]
ordenou um re-exame do processo contra
Galileo, o que acabou por eliminar os últimos vestígios de
resistência, por parte da igreja Católica, à revolução Copernicana.
Galileo foi perdoado em 31 de outubro de 1992.
![]() Simulação das Leis de Kepler
Simulação das Leis de Kepler
![]() Newton
Newton
![]() Astronomia e Astrofísica
Astronomia e Astrofísica
![]()