Próxima: Lei de Wien

Apêndice: Teoria da Radiação

Em 1900, o físico alemão Max K.E.L. Planck (1858-1947) postulou que a energia eletromagnética só pode se propagar em quanta discretos, ou fótons, cada um com energia E = h$\nu$. Com esta quantização da energia, ele pode derivar a intensidade de um campo de radiação.

A intensidade específica monocromática (energia por unidade de comprimento de onda, por segundo, por unidade de área, e por unidade de ângulo sólido) de um corpo que tem uma temperatura uniforme T e está em equilíbrio termodinâmico com sua própria temperatura (isto é, é opaco) é chamada B_$\lambda$(T) e é dada pela Lei de Planck:

B_$\lambda$(T)d$$\lambda$$ = - $${\frac{cE}{4\pi}}$$dn_b(p),

onde E é a energia da partícula, e dn_b(p) é a distribuição de momentum p de Bose-Einstein de um gás de bósons de spin s:

dn_b(p) = $${\frac{(2s+1)}{exp[(E-C)/kT]-1}}$$$${\frac{4\pi p^2dp}{h^3}}$$,

onde

C $$\equiv$$ $${\frac{\mu}{kT}}$$,

sendo $\mu$ o potencial químico, é um número real que depende da densidade de partículas (número de partículas por unidade de volume N), e é obtido integrando-se:

N = $$\int^{\infty}_{0}$$n(p)dp.

O termo (2s + 1) representa o número de partículas (estados independentes) possíveis com mesma energia E, e o termo h³ é necessário devido ao princípio da incerteza de Heisenberg que define o menor tamanho possível da célula para o produto do volume de espaço e de momentum.

Para um fóton, que é um bóson de massa zero e spin 1, E = h$\nu$, p = h$\nu$/c, $\lambda$ = c/$\nu$ e C = 0. Com estes valores se pode obter:

$$\boxed$$B_$\lambda$(T)=$${\frac{2hc^2}{\lambda^5}}$$$${\frac{1}{e^{hc/\lambda kT}-1}}$$,

onde h = 6, 63×10^-27ergs/s é a constante de Planck, e k = 1, 38×10^-16ergs/K é a constante de Boltzmann [(em honra ao austríaco Ludwig Boltzmann (1844-1906)].

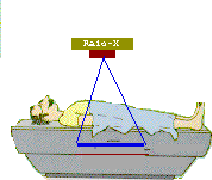
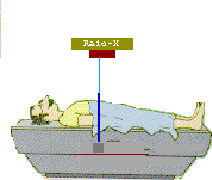Esta intensidade específica não depende de qualquer propriedade do corpo a não ser sua temperatura. Qualquer corpo em equilíbrio termodinâmico emitirá fótons com uma distribuição de comprimentos de onda dada pela Lei de Planck acima. Esta radiação, chamada de radiação de corpo negro, não depende da direção de emissão, e não é polarizada.

Imagens
Subsections

• Lei de Wien
• Lei de Stefan-Boltzmann

Próxima: Lei de Wien