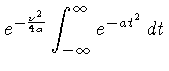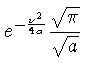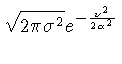


Próxima: Restauração da Imagem
Volta: Transformadas de Fourier
Anterior: Rotação
Gaussiana
Uma função gaussiana é definida como:
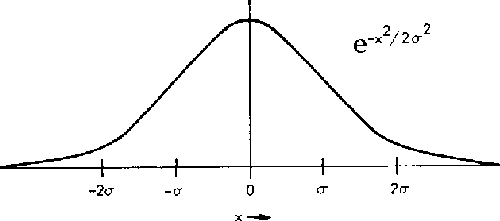
como na figura abaixo,
e 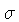 mede a meia largura a uma altura de 1/e.
mede a meia largura a uma altura de 1/e.
A área da curva sob a gaussiana é dada por:
Na teoria de probabilidades, a distribuição normal é
dada por:
que é uma função gaussiana normalizada para área unitária.
O termo 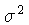 é chamado de variança, e
é chamado de variança, e 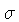 é o desvio médio padrão.
é o desvio médio padrão.
A gaussiana tem uma propriedade muito útil; a convolução
de duas funções gaussianas é também uma gaussiana.
onde
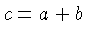
e
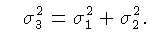
A gaussiana resultante da convolução de duas gaussianas é alargada - seu desvio padrão médio é
a raiz quadrada da soma das varianças originais. A gaussiana
é utilizada para modelar o efeito de largura do feixe, e sistemas
ópticos sobre a imagem.
Note que nesta derivação utilizamos a frequência 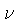 linear,
e não angular
linear,
e não angular
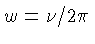 .
.



Próxima: Restauração da Imagem
Volta: Transformadas de Fourier
Anterior: Rotação
©
Modificada em 25 maio 2008
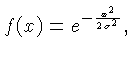
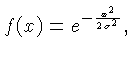
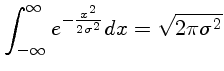
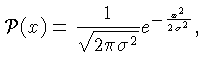
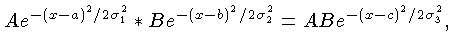
![$\displaystyle {\cal{F}}\left[e^{-\frac{x^2}{2\sigma^2}}\right] \equiv {\cal{F}}\left[e^{-ax^2}\right]$](img370.gif)
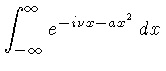
![$\displaystyle \int_{-\infty}^\infty
\exp\left[-a\left(x+\frac{i\nu }{2a}\right)^2 - \frac{\nu ^2}{4a}\right]\,dx$](img372.gif)