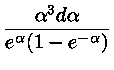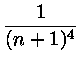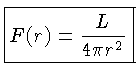

Volta: Apêndice: Teoria da Radiação
Anterior: Lei de Wien
Lei de Stefan-Boltzmann
O fluxo (energia por unidade de área, por segundo) de
um corpo negro de temperatura T é dado por:
F = 2
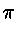
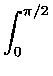
cos
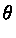
sin
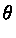
d
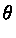
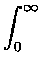 B
B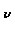
(
T)
d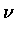
=
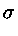 T4
T4,
onde
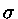 = 5, 67×10-5ergs cm-2 K-4 s-1
é a constante de Stefan-Boltzmann, já que:
e definindo-se
alpha
= 5, 67×10-5ergs cm-2 K-4 s-1
é a constante de Stefan-Boltzmann, já que:
e definindo-se
alpha 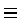
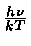 ,
,
| B(T) |
= |
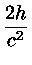 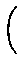 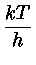 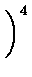 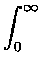 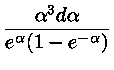 |
(1.1) |
| |
= |
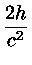  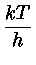 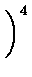 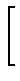 6 6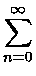 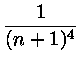 ![$\displaystyle \left.\vphantom{6 \sum_{n=0}^\infty
\frac{1}{(n+1)^4}}\right]$](img37.gif) |
(1.2) |
| |
= |
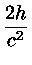  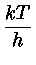 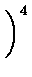 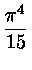 . . |
(1.3) |
A energia que atinge o detector por unidade de área e de tempo,
por definição de
fluxo, é de:
onde r é a distância da fonte ao detector.


Volta: Apêndice: Teoria da Radiação
Anterior: Lei de Wien
 Imagens
Imagens

kepler@if.ufrgs.br
Modificada em 1999-10-29
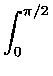 cos
cos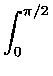 cos
cos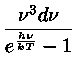 ,
,