FIS2001 - Lista de Exercícios 1

Esfera celeste, Sistemas de coordenadas, Movimento anual do Sol, Fases da Lua, Eclipses

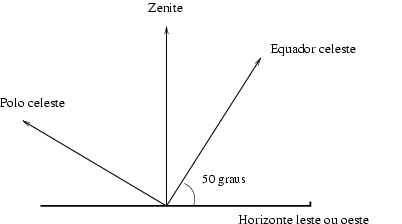
1. Como os círculos diúrnos das estrelas são sempre paralelos ao equador, se eles fazem um ângulo de 50 ^o com o horizonte, é porque o equador encontra-se inclinado de 50 ^o em relação ao horizonte (ver ilustração abaixo). Logo o equador faz um ângulo de 40^o com o Zênite, e o pólo elevado faz um ângulo de 40^o com o horizonte. Como a latitude do lugar é igual à algura do pólo elevado (= ângulo que o pólo elevado faz com o horizonte) que é igual à declinação do zênite ( ângulo entre o equador e o zênite), por qualquer uma das definições vemos que neste caso a latitude é 40^o
2. o pólo sul, a uma altura de 40^o

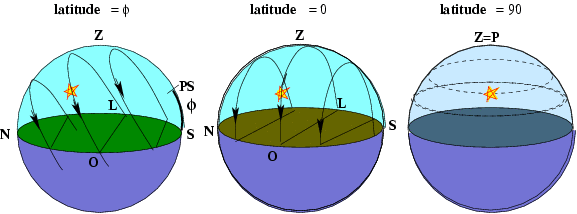
1. A altura do pólo é igual à latitude do local. No Equador, Φ=0°, h_P=0^o, o pólo está no horizonte. No pólo o zênite está no pólo, e o equador no horizonte.
2. 0^o
3. As estrelas giram em torno do polo, que está no horizonte. Todas nascem e se põem perpendiculamente ao horizonte
4. não

São aquelas que têm declinação negativa (pertencem ao hemisfério sul), e maior do que 31^o (90^o - 59^o), ou seja, Canopus, Acrux e Rigelkent.

São aquelas que têm declinação negativa, e maior em módulo do que 60^o (90^o - 30^o): Rigelkent e Acrux.

É aquela que tem a declinação mais próxima da latitude de Porto Alegre, ou seja, Antares.

Em um dia a terra percorre aproximadamente um grau em torno do sol (pois em 365,25 dias percorre 360 graus). Com isso, a terra deve girar um grau a mais em torno de seu eixo para retornar à mesma posiçao relativa ao sol, e assim completar 1 dia solar. O tempo que ela leva para girar 1 grau em torno de seu eixo é de 4 minutos (pois leva 24h para girar 360 graus). Ver figura abaixo.
2. O ângulo entre o equador e o zênite, em Montreal, é 48^°. Portanto o equador fica a uma altura de 90^° - 48^° = 42^o. O Sol, no verão ,e stá 23,5^o ao norte do equador. Portanto, em relação ao horizonte, sua altura é
  h_max = 42^o + 23,5^o = 65,5^o
3. Se em Porto Alegre a máxima altura do Sol, no verão, é 83,5 ^o, calcula a razão entre a insolação recebida em Montreal, no verão, com a insolação recebida em Porto Alegre, no verão. I_M/I_PA = sen 65,5^o/sen 83,5^o = 0,916
4. (a) em Montreal
  As diferenças entre inverno e verão seriam bem mais acentuadas, pois Montreal estaria a apenas a 9^o do círculo polar Ártico (que estaria à latitude de 57^o), portanto as noites no inverno seriam ainda mais longas, e ainda mais curtas no verão.
  (b) em uma cidade localizada no equador
  No equador a diferença não seria tão grande, pois os dias continuariam a ter 12h todo o ano, apenas a máxima altura do Sol variaria de 90^o a 57^o, comparada com a variação real de 90^o a 66,5^o.

(a) Porque nas outras fases lunares, o sol, a terra e a lua não se encontram alinhados. (b)Na lua nova ocorre eclipse solar e na lua cheia ocorre eclipse lunar. (c)Porque existe uma inclinaçao de 5 graus entre o plano da órbita da lua e a eclíptica. (d) Haveriam eclipses solares e lunares.