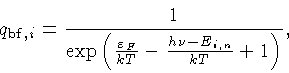Próxima: Transições Livre-Livre
Volta: Opacidades
Anterior: Opacidades
As transições ligado-livres somente ocorrem se a radiação tiver
freqüência superior àquela necessária para remover o elétron
da camada em que ele se encontra, para um átomo de um elemento
presente no meio. Se designarmos 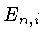 como a energia do átomo
ou íon de tipo
como a energia do átomo
ou íon de tipo 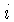 , a partir do nível de energia de número
quântico
, a partir do nível de energia de número
quântico 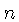 , então a absorção ocorrerá
para os fótons com freqüência superior a
, então a absorção ocorrerá
para os fótons com freqüência superior a
onde 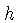 é a constante de Planck. O excesso de energia do
fóton,
é a constante de Planck. O excesso de energia do
fóton,
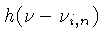 , aparecerá como energia cinética
do elétron emitido. Em 1923 Kramers derivou a fórmula
para o coeficiente de absorção ligado-livre e livre-livre
para transições por raio-X, por elétron na camada
, aparecerá como energia cinética
do elétron emitido. Em 1923 Kramers derivou a fórmula
para o coeficiente de absorção ligado-livre e livre-livre
para transições por raio-X, por elétron na camada 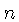 . Para freqüências acima da freqüência de corte, o
coeficiente de absorção por partícula será dado por:
. Para freqüências acima da freqüência de corte, o
coeficiente de absorção por partícula será dado por:
|
|
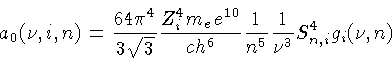 |
(1.63) |
para 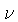 em Hertz.
em Hertz.
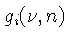 é o fator de
Gaunt,
que precisa ser calculado usando-se a mecânica quântica, e representa
a correção quântica à derivação semi-clássica de Kramers.
O fator de
Gaunt foi publicado por
John Arthur Gaunt (1904-1944)
que
fora estudante de Ralph Howard Fowler (1889-1944),
em 1930,
no artigo Continuous Absorption, no
Philosophical Transactions of the Royal Society of London, Series A, 229, 163,
para várias situações.
Esta correção é próxima de um e varia lentamente com a freqüência.
O fator correção
é o fator de
Gaunt,
que precisa ser calculado usando-se a mecânica quântica, e representa
a correção quântica à derivação semi-clássica de Kramers.
O fator de
Gaunt foi publicado por
John Arthur Gaunt (1904-1944)
que
fora estudante de Ralph Howard Fowler (1889-1944),
em 1930,
no artigo Continuous Absorption, no
Philosophical Transactions of the Royal Society of London, Series A, 229, 163,
para várias situações.
Esta correção é próxima de um e varia lentamente com a freqüência.
O fator correção 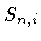 , chamado de
fator de escudamento
( screening factor),
leva em conta que a carga real vista pelas partículas é
, chamado de
fator de escudamento
( screening factor),
leva em conta que a carga real vista pelas partículas é
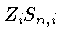 , menor do que
, menor do que 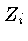 , pois os elétrons livres formam
uma nuvem entre os íons, reduzindo sua carga efetiva.
Este fator também corrige pela redução da carga nuclear efetiva devido
à existência, se for o caso, de elétrons em camadas mais internas do que
a em considereção, e mesmo de outros elétrons na mesma camada.
, pois os elétrons livres formam
uma nuvem entre os íons, reduzindo sua carga efetiva.
Este fator também corrige pela redução da carga nuclear efetiva devido
à existência, se for o caso, de elétrons em camadas mais internas do que
a em considereção, e mesmo de outros elétrons na mesma camada.
Para o ionização do hidrogênio a partir do estado fundamental
onde 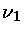 é a freqüência de referência (limite de Lyman),
e o fator de Gaunt varia de 0,797 para 912Å, a 0,515 para 9,12Å.
é a freqüência de referência (limite de Lyman),
e o fator de Gaunt varia de 0,797 para 912Å, a 0,515 para 9,12Å.
Como um exemplo,
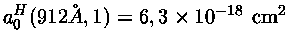 ,
já que a freqüência correspondente a
,
já que a freqüência correspondente a
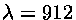 Å é
Å é
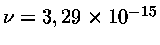 Hz.
Hz.
Entre as bordas de absorção, isto é, para n=constante,
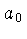 varia aproximadamente como
varia aproximadamente como 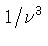 .
.
Se o gás estiver parcialmente degenerado, um fator adicional
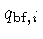 precisa ser introduzido para levar em conta
que a célula do espaço de fase correspondente ao estado final (livre)
do elétron pode já estar ocupada por outro elétron.
precisa ser introduzido para levar em conta
que a célula do espaço de fase correspondente ao estado final (livre)
do elétron pode já estar ocupada por outro elétron.
ou seja, podemos substituir o fator de Gaunt acima por





Próxima: Transições Livre-Livre
Volta: Opacidades
Anterior: Opacidades
©
Modificada em 3 abril 2009
![]() como a energia do átomo
ou íon de tipo
como a energia do átomo
ou íon de tipo ![]() , a partir do nível de energia de número
quântico
, a partir do nível de energia de número
quântico ![]() , então a absorção ocorrerá
para os fótons com freqüência superior a
, então a absorção ocorrerá
para os fótons com freqüência superior a
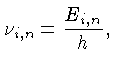
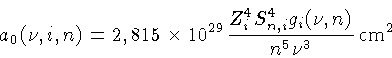
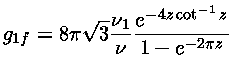
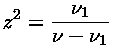
![]() ,
já que a freqüência correspondente a
,
já que a freqüência correspondente a
![]() Å é
Å é
![]() Hz.
Hz.
![]() varia aproximadamente como
varia aproximadamente como ![]() .
.
![]() precisa ser introduzido para levar em conta
que a célula do espaço de fase correspondente ao estado final (livre)
do elétron pode já estar ocupada por outro elétron.
precisa ser introduzido para levar em conta
que a célula do espaço de fase correspondente ao estado final (livre)
do elétron pode já estar ocupada por outro elétron.