
 A teoria eletrofraca padrão, desenvolvida independentemente por
Sheldon Glashow (1932-),
Steven Weinberg (1933-2021) &
Abdus Salam (1926-1996)
preve que os neutrinos não têm massa.
Isto ocorre por que o modelo padrão, baseado no grupo unitário SU3, contém somente neutrinos orientados pela regra da mão esquerda.
Sem contrapartes orientados pela regra da mão direita, não é possível adicionar um termo de massa renormalizável
ao modelo padrão.
Teorias de grande unificação (GUT) baseadas em grandes
grupos, como o grupo unitário SU5 ou o grupo ortogoinal SO10, geralmente prevêm neutrinos com massa.
Partículas Majorama [Ettore Majorana (1906-1938), 1937, Nuovo Cimento, 14, 171] são indistingüíveis de suas
antipartículas, enquanto partículas de Dirac são diferentes de suas antipartículas. Os neutrinos de
Dirac podem ter momentum magnético, mas os Majorana não.
No artigo de 2014,
Constraining the neutrino magnetic dipole moment from white dwarf pulsations,
publicado no Journal of Cosmology and Astroparticle Physics, Issue 08, article id. 054,
Alejandro Hugo Córsico, Leandro Gabriel Althaus, Marcelo
Miguel Miller Bertolami, S.O. Kepler & Enrique Garcia-Berro,
usam a taxa de variação do período de pulsação da anã branca DBV PG 1351+489 para colocar limite no momento de dipolo magnético do neutrino,
comparáveis aos limites estabelecidos pela função de luminosidade
das anãs brancas e pelo diagrama cor-magnitude do aglomerado
globular M5 observados.
Ralph Asher Alpher (1921-2007),
James W. Follin Jr. (1920-2007),
e Robert C. Herman (1922-1997), em 1953, no Physical Review, 92, 1347,
explicitaram que a natureza da espécie de neutrinos
(Dirac versus Majorana) afeta a razão de congelamento de nêutrons-para-prótons,
n/p, e portanto a abundância primordial de hélio.
A massa máxima do neutrino pode ser estimada da diferença de
massa entre o trítio e o
3He.
No decaimento do trítio, a massa do neutrino limita a energia máxima
do 3He,
que é 65,4 eV para os átomos neutros, mas precisamos corrigir pela energia dos elétrons, que
chega a 27,2 eV para o trítio e 40,8 eV (25%) ou 48,4 eV (1,4%), em relação ao estado
fundamental, que ocorre em 70% dos casos.
O limite para a massa do neutrino do
elétron, pelo decaimento do trítio é
2,2 eV, com 95% de certeza
(Neutrino muon: m < 170 keV,
neutrino tau: m < 15.5 MeV).
A teoria eletrofraca padrão, desenvolvida independentemente por
Sheldon Glashow (1932-),
Steven Weinberg (1933-2021) &
Abdus Salam (1926-1996)
preve que os neutrinos não têm massa.
Isto ocorre por que o modelo padrão, baseado no grupo unitário SU3, contém somente neutrinos orientados pela regra da mão esquerda.
Sem contrapartes orientados pela regra da mão direita, não é possível adicionar um termo de massa renormalizável
ao modelo padrão.
Teorias de grande unificação (GUT) baseadas em grandes
grupos, como o grupo unitário SU5 ou o grupo ortogoinal SO10, geralmente prevêm neutrinos com massa.
Partículas Majorama [Ettore Majorana (1906-1938), 1937, Nuovo Cimento, 14, 171] são indistingüíveis de suas
antipartículas, enquanto partículas de Dirac são diferentes de suas antipartículas. Os neutrinos de
Dirac podem ter momentum magnético, mas os Majorana não.
No artigo de 2014,
Constraining the neutrino magnetic dipole moment from white dwarf pulsations,
publicado no Journal of Cosmology and Astroparticle Physics, Issue 08, article id. 054,
Alejandro Hugo Córsico, Leandro Gabriel Althaus, Marcelo
Miguel Miller Bertolami, S.O. Kepler & Enrique Garcia-Berro,
usam a taxa de variação do período de pulsação da anã branca DBV PG 1351+489 para colocar limite no momento de dipolo magnético do neutrino,
comparáveis aos limites estabelecidos pela função de luminosidade
das anãs brancas e pelo diagrama cor-magnitude do aglomerado
globular M5 observados.
Ralph Asher Alpher (1921-2007),
James W. Follin Jr. (1920-2007),
e Robert C. Herman (1922-1997), em 1953, no Physical Review, 92, 1347,
explicitaram que a natureza da espécie de neutrinos
(Dirac versus Majorana) afeta a razão de congelamento de nêutrons-para-prótons,
n/p, e portanto a abundância primordial de hélio.
A massa máxima do neutrino pode ser estimada da diferença de
massa entre o trítio e o
3He.
No decaimento do trítio, a massa do neutrino limita a energia máxima
do 3He,
que é 65,4 eV para os átomos neutros, mas precisamos corrigir pela energia dos elétrons, que
chega a 27,2 eV para o trítio e 40,8 eV (25%) ou 48,4 eV (1,4%), em relação ao estado
fundamental, que ocorre em 70% dos casos.
O limite para a massa do neutrino do
elétron, pelo decaimento do trítio é
2,2 eV, com 95% de certeza
(Neutrino muon: m < 170 keV,
neutrino tau: m < 15.5 MeV).
Um reator nuclear com potência térmica de 2800 MW emite cerca de
![]() /s,
com energias até 8 MeV, vindos principalmente (69%) do decaimento do
/s,
com energias até 8 MeV, vindos principalmente (69%) do decaimento do ![]() . As oscilações
entre os neutrinos tipo i e j são periódicas com um comprimento de onda L, em que a fase
muda por 2π, no vácuo, de
. As oscilações
entre os neutrinos tipo i e j são periódicas com um comprimento de onda L, em que a fase
muda por 2π, no vácuo, de
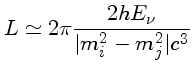
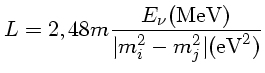
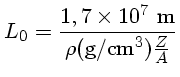
![$ L_m=L\left[1+\left(\frac{L}{L_0}\right)^2+\frac{2L}{L_0}\cos 2\theta\right]^{-\frac{1}{2}}$](img19.png)
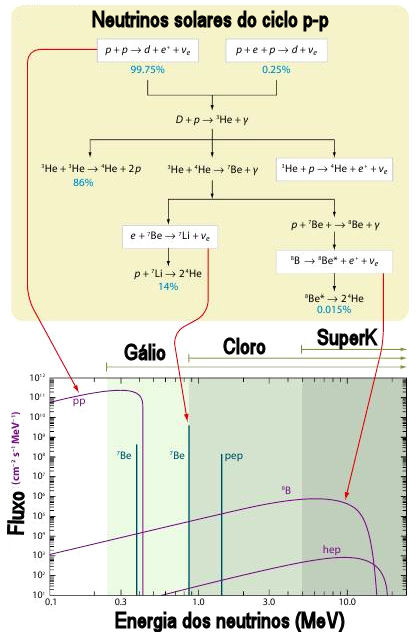
Nos experimentos, os neutrinos são detectados por
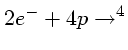 He
HeNo Kamiokande, o elétron espalhado pelo neutrino sai na mesma direção do neutrino incidente, indicando a direção da fonte.
Embora os neutrinos do muon e do taon só interajam por correntes neutras (troca de ![]() ), os
neutrinos dos elétrons interagem com elétrons também por correntes carregadas (troca de
), os
neutrinos dos elétrons interagem com elétrons também por correntes carregadas (troca de
![]() ).
).
Os experimentos solares são compatíveis com oscilações de neutrinos se
![]() -
-![]() eV
eV![]() , desde que
, desde que
![]() .
Ko Abe e colaboradores publicaram em 2011,
no
Physical Review D, 83, 052010, os resultados dos
dados de 2002 a 2010, com um total de 8132 neutrinos detectados no
SuperKamiokande,
concluindo, com
um nível de confiança de 99,99%,
que a não detecção dos neutrinos faltantes somente é consistente
com a oscilaçao de neutrinos, isto é, na transformação dos neutrinos,
após produzidos e antes de serem detectados, de neutrinos de
elétrons para neutrinos de múons ou de táons, com
.
Ko Abe e colaboradores publicaram em 2011,
no
Physical Review D, 83, 052010, os resultados dos
dados de 2002 a 2010, com um total de 8132 neutrinos detectados no
SuperKamiokande,
concluindo, com
um nível de confiança de 99,99%,
que a não detecção dos neutrinos faltantes somente é consistente
com a oscilaçao de neutrinos, isto é, na transformação dos neutrinos,
após produzidos e antes de serem detectados, de neutrinos de
elétrons para neutrinos de múons ou de táons, com
![]() m2,1=7,6±0,02 meV,
com ângulo de mistura sen2θ1,2=0,31±0,01,
enquanto sen2θ1,3<0,060 com 95% de confiança.
Nesta nomenclatura, 1=νe, 2=νμ e 3=ντ.
m2,1=7,6±0,02 meV,
com ângulo de mistura sen2θ1,2=0,31±0,01,
enquanto sen2θ1,3<0,060 com 95% de confiança.
Nesta nomenclatura, 1=νe, 2=νμ e 3=ντ.
Maria Concepion Gonzalez-Garcia, Michele Maltoni e Jordi Salvado, no artigo de revisão de 2011 Updated global fit to three neutrino mixing: status of the hints of θ1,3>0, discutem que ainda não há provas suficientes de que o neutrinos dos elétrons e táons se misturam diretamente.
Se os neutrinos estavam em equilíbrio com os fótons no início do Universo, podemos calcular a densidade de bósons e férmions ultrarelativísticos:
ondeAs densidades de energia são dadas por:
Conseqüentemente, de (1) e (2), enquanto estiverem em equilíbrio, o número de cada neutrino Majorana é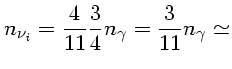
Referências: