Efeito Zeeman

A energia em um campo magnético B em um esfera de raio R é dada por

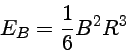
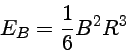
$E_B=\frac{1}{6}B^2 R^3$

A pressão magnética

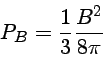
$P_B=\frac{1}{3}\frac{B^2}{8\pi}$

resulta da ordem de $P_B\simeq 1 \times 10^{18}$ dinas/cm

, comparada com a pressão do gás, hidrostática,

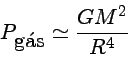
$P_{gás}\simeq \frac{GM^2}{R^4}$

da ordem de $4 \times 10^{23}$ dinas/cm

para o interior de uma anã branca. A densidade de energia potencial magnética é dada por

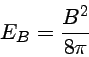
$E_B=\frac{B^2}{8\pi}$

no sistema cgs e

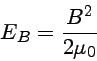
$E_B=\frac{B^2}{2\mu_0}$

no sistema mks, onde $\mu_0$ é a permeabilidade do espaço livre, uma constante valendo $4\pi\times 10^{-7}$ weber/(ampere.metro).

Quando um elétron atômico está em um campo magnético, o Hamiltoniano tem termos adicionais

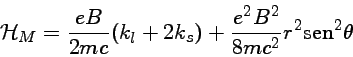
$\cal{H}}_M = \frac{eB}{2mc}(k_l+2 k_s) + \frac{e^2B^2}{8mc^2}r^2 \mbox{sen}^2 \theta$

onde

são os operadores momento angular orbital e de spin projetados ao longo do campo, e

e $\theta$ são coordenadas polares em relação à direção do campo. Como $\Delta s=0$ para transições de dipolo elétrico, o spin não tem efeito no espectro e pode ser ignorado.

O primeiro termo no Hamiltoniano produz tripletos de Lorentz ( $\Delta m_l=0,\pm 1$ , com uma separação da ordem de 10Å/MG em 4500Åe 20,115Å/MG em H $\alpha$ . Para campos acima de 10MG o efeito quadrático precisa ser levado em conta, e o termo linear pode ser comparado com o quadrático

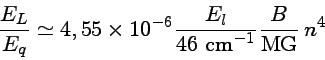
$\frac{E_L}{E_q}\simeq 4,55 \times 10^{-6}\frac{E_l}{\mbox{46 cm$^{-1}$}} \frac{B}{\mbox{MG}}\,n^4$

de modo que para um campo de 10 MG, o termo quadrático é pequeno para H $\alpha$ , mas igual ao efeito linear para H $\gamma$ e dominante para os níveis mais altos. O termo quadrático é sempre positivo, deslocando para o azul.

Para átomos com linhas singletos (S=0), um campo magnético fraco separa cada nível em 2J+1 níveis igualmente espaçados, onde J é o momento angular total (m_l+m_s). De acordo as observações do físico holandês Pieter Zeeman (1865-1943) (1897, "The Effect of Magnetisation on the Nature of Light Emitted by a Substance", Nature, 55, 347) e a explicação teórica de seu professor Hendrik Antoon Lorentz (1853-1928) (1897), os níveis de energia são dados por

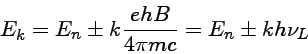
$E_k = E_n \pm k\frac{ehB}{4\pi mc} = E_n \pm k h \nu_L$

para valores de k inteiros entre 0 e J,

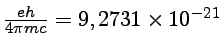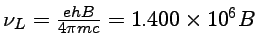é o valor da energia sem o campo magnético, B é a intensidade do campo magnético, o fator $\frac{eh}{4\pi mc}=9,2731 \times 10^{-21}$ ergs/gauss é o momento de Bohr do magnetron, e $\nu_L=\frac{ehB}{4\pi mc}=1.400 \times 10^6 B$ Hz é a freqüência de Larmor de precessão do elétron em torno do campo magnético, para B dado em gauss [Sir Joseph Larmor (1857-1942), 1897, "The Influence of a Magnetic Field on Radiation Frequency". Proceedings of the Royal Society of London, 60, 514, Zeeman e Lorentz receberam o prêmio Nobel de 1902 pela descoberta do efeito Zeeman.

As regras de seleção para as transições permitidas entre os diferentes níveis são $\Delta k=0,\pm 1$ , e um nível com k=0 não pode se combinar com outro nível de k=0. Como o espaçamento é igual para todos os componentes, cada nível de um singleto se separa em tres componentes, a componente $\pi$ com a mesma freqüência inicial, e as duas componentes $\sigma$ deslocadas pela freqüência de Larmor. A componente $\pi$ é plano polarizada no plano contendo a linha de visada e o vetor do campo magnético. As duas componentes $\sigma$ são polarizadas elípticamente. Nas observações na direção do campo magnético, a componente central $\pi$ não é detectada e as duas componentes $\sigma$ serão circularmente polarizadas em direções opostas de rotação, com a de mais baixa freqüência sendo a com rotação horária). Na direção perpendicular ao campo, as três componentes são visíveis, mas a central mostra polarização linear paralela ao campo e as outras duas mostram polarização linear perpendicular ao campo.

A intensidade observada dependerá da intensidade que seria produzida se não houvesse campo magnético, da inclinação $\theta$ do vetor campo magnético com a linha de visada, e das características de polarização do detector. O americano Frederick Hanley Seares (1873-1964) calculou as intensidades dos feixes com polarização circular (1913, Astrophysical Journal, 38, 99). Os campos magnéticos no Sol têm de um a centenas de gauss [Horace Wellcome Babcock (1912-2003) e Harold Delos Babcock (1882-1968), 1955, Astrophysical Journal, 121, 349] e o meio interestelar de $1\mu$ G.

De acordo com George W. Preston (1970, Astrophysical Journal, 160, L143):

$\Delta \lambda_{\mbox{linear}} (\mbox{\AA}) = \pm 4,67 \times 10^{-13} \lambda^2 B$

que corresponde a 20 Å/MG em Hα

Quando o campo é fraco e o spin é diferente de zero, ocorre o efeito Zeeman anômalo, por acoplamento spin-órbita, com os níveis de energia calculados por Thomas Preston (1860-1900) ['Radiation phenomena in a strong magnetic Magnetic Field', Proceedings Royal Society, 63 (1898)] e Alfred Landé (1888-1976) em 1920 e 1923, como

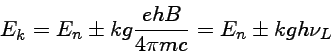
$E_k = E_n \pm kg\frac{ehB}{4\pi mc} = E_n \pm kg h \nu_L$

com o fator de Landé, g, dado por [G.E. Uhlenbeck & S. Goudsmit, Naturwissenschaften 47 (1925) 953; Nature 117 (1926) 264]:

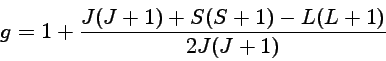
$g = 1 + \frac{J(J+1)+S(S+1)-L(L+1)}{2J(J+1)}$

onde J é o momento angular total, S o momento angular de spin e L o momento angular orbital.

O número de componentes depende de J, L e S dos níveis superiores e inferiores. As observações perpendiculares ao campo mostram a componente $\pi$ linearmente polarizada paralela ao campo e as componentes $\sigma$ linearmente polarizadas perpendicular ao campo, enquanto que as observações paralelas ao campo mostram somente as componentes $\sigma$ , circularmente polarizadas.

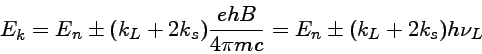
$E_k = E_n \pm (k_L+2k_s)\frac{ehB}{4\pi mc} = E_n \pm (k_L+2k_s) h \nu_L$

onde os números quânticos

assumem valores entre $\pm L$ e $\pm S$ respectivamente, e as regras de seleção são $\Delta k_L=0,\pm 1$ e $\Delta k_S=0$ .

O termo quadrático do deslocamento Zeeman para o hidrogênio (F.A. Jenkins & E. Segré 1939, Physical Review, 55, 52) será da ordem de

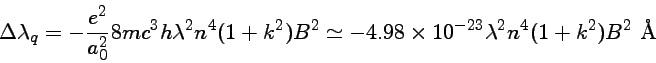
$\Delta \lambda_q \simeq -4,98 \times 10^{-23} \lambda^2 n^4 (1+k^2)B^2~\mbox{\AA}$

onde

é o raio da primeira órbita de Bohr, n o número quântico principal e k o número quântico magnético (m_l+m_s) do nível superior.

Para as linhas de Balmer do hidrogênio, o deslocamento do centróide da componente $\sigma$ ( $m_l=\pm 1$ ) é o dobro daquela da componente $\pi$ (). O deslocamento quadrático da centróide será

$\langle \Delta \lambda_q\rangle = -7,5 \times 10^{-23} \lambda^2 n^4 B^2~\mbox{\AA}$

Por exemplo, $\langle \Delta \lambda_q\rangle=0,25$ Åpara H $\alpha$ e 0,45 Åpara H $\beta$ em um campo de 1 MG.

De acordo com Anders Blom enquanto no sistema não perturbado os números quânticos são n, $\ell$ , $m_\ell$ e , de spin, com os estados degenerados em $m_\ell$ e , na presença de um campo magnético externo os $m_\ell$ e não são mais bons números quânticos, mas sim sua soma, $m=m_\ell + m_s$ . Desta forma, para $\ell=1$ , $m_\ell=\pm 1,0$ e $m_s=\pm 1/2$ , teremos quatro estados, com m=± 3/2 e ± 1/2.

Para um átomo hidrogênico,

$\Delta E_{n\ell m} = E_0 + \Delta E_{rel} + \Delta E_{\ell m}(B) + \Delta E_{Darwin}\delta_{\ell 0}$

onde

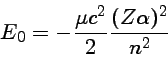
$E_0 = - \frac{\mu c^2}{2} \frac{(Z\alpha)^2}{n^2}$

é a energia não perturbada, $\mu$ a massa reduzida do elétron,

$\Delta E_{rel} = \frac{1}{2}m_e c^2 \frac{(Z\alpha)^2}{n^4}[\frac{3}{4}-\frac{n}{\ell+1/2}]$

Para $\ell=0$ o termo Darwin precisa ser incluído

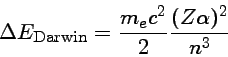
$\Delta E_{Darwin} = \frac{m_e c^2}{2}\frac{(Z\alpha)^2}{n^3}$

e a contribuição linear para a energia devido à interação do campo magnético com o spin-órbita é

$\begin{eqnarray} \Delta E_{\ell m}(B) &=&W [\ell \pm (\ell +1)\frac{B}{B_0}] \quad |m| = \ell+\frac{1}{2}, \ell \neq 0\cr &=&\frac{W}{2}[ 2m\frac{B}{B_0} - 1 \pm \sqrt{(\frac{B}{B_0})^2 + 4m \frac{B}{B_0} + (2\ell+1)^2} \quad |m| = \ell-\frac{1}{2}, \ell \neq 0\cr &=&\pm B \mu_B \quad \ell=0 \end{eqnarray}$

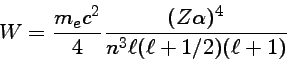onde $W = \frac{m_e c^2}{4} \frac{(Z\alpha)^4}{n^3\ell(\ell+1/2)(\ell+1)}$ e

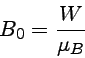
$B_0 = \frac{W}{\mu_B}$

é o campo interno, da ordem de 1 tesla =

gauss para um átomo de hidrogênio. A solução para campo forte $B/B_0 \gg (2\ell+1)$ não depende de $\ell$ ,

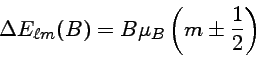
$\Delta E_{\ell m}(B) = B \mu_B (m \pm \frac{1}{2})$

é chamada de efeito Zeeman normal e não depende de $\ell$ , enquanto a solução de campo fraco é chama de efeito Zeeman anômalo. $\mu_B$ é o momento magnético do elétron.

As regras de seleção são

$\Delta m_s = 0 \quad\quad \Delta \ell=1 \quad\quad \Delta m_\ell = 0,\pm 1$

Astronomia e Astrofísica