Escudamento eletrônico
A principal modificação que precisamos fazer à discussão
de reações nucleares apresentada até agora é
a alteração ao potencial de Coulomb entre os reagentes,
devido à presença dos elétrons no meio. Esse problema
é chamado de electron screening.
Considere dois reagentes totalmente ionizados e de mesma carga Z.
Podemos definir o raio de Wigner-Seitz 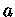 [Eugene Paul Wigner (1902-1995) e Fredrick Seitz (1911-2008)], de modo que
[Eugene Paul Wigner (1902-1995) e Fredrick Seitz (1911-2008)], de modo que
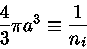 |
(1) |
onde 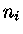 é a densidade de íons, por número. Se
é a densidade de íons, por número. Se
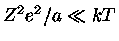 ,
a teoria de Debye-Hückel
[Peter Josef William Debye (1884-1966) e
Erich Hückel (1896-1980)]
nos diz que o potencial eletrostático
de um íon, circundado por uma nuvem de elétrons, é dado por:
,
a teoria de Debye-Hückel
[Peter Josef William Debye (1884-1966) e
Erich Hückel (1896-1980)]
nos diz que o potencial eletrostático
de um íon, circundado por uma nuvem de elétrons, é dado por:
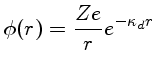 |
(2) |
onde 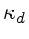 , o inverso do raio de Debye, é dado por:
, o inverso do raio de Debye, é dado por:
![\kappa_d = [\frac{4\pi e^2}{kT}(Z^2n_i+n_e)]^{1/2}](img7.gif) |
(3) |
O efeito da exponencial é o de reduzir a barreira de potencial abaixo
do seu valor coulombiano 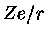 , para um dado valor de
, para um dado valor de 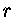 .
Como estamos interessados em calcular como esse potencial modificado
afeta a barreira de penetrabilidade, o valor de
.
Como estamos interessados em calcular como esse potencial modificado
afeta a barreira de penetrabilidade, o valor de 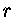 de interesse é da ordem de
de interesse é da ordem de
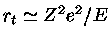 , onde
, onde 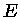 é a energia
cinética para separação infinita. Se usarmos o valor
de
é a energia
cinética para separação infinita. Se usarmos o valor
de 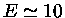 KeV do pico de Gamow,
e Z unitário, obtemos o valor de
KeV do pico de Gamow,
e Z unitário, obtemos o valor de
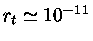 cm. Portanto, para valores pequenos de
cm. Portanto, para valores pequenos de
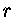 , podemos aproximar
, podemos aproximar
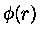 como
como
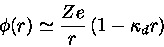 |
(4) |
de modo que a barreira potencial eletrostática
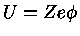 fica reduzida por uma quantia
fica reduzida por uma quantia
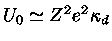 devido à presença da nuvem eletrônica circundante.
Portanto, podemos, em princípio, substituir
devido à presença da nuvem eletrônica circundante.
Portanto, podemos, em princípio, substituir
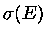 por
por 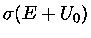 , ou seja
, ou seja
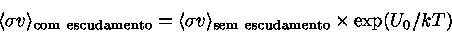 |
(5) |
Como 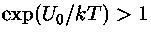 , há aceleração na taxa de
reação nuclear. Por exemplo, para X=0,7 e Y=0,3, isto é,
desprezando os outros íons, obtemos para o ciclo pp no centro do Sol
, há aceleração na taxa de
reação nuclear. Por exemplo, para X=0,7 e Y=0,3, isto é,
desprezando os outros íons, obtemos para o ciclo pp no centro do Sol
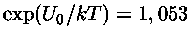 .
Para a reação de prótons com
.
Para a reação de prótons com
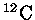 em uma estrela de população I, com
em uma estrela de população I, com 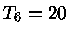 e
e
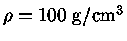 ,
encontramos
,
encontramos
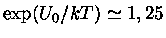 . Portanto, o efeito do
escudamento é significativo.
. Portanto, o efeito do
escudamento é significativo.


 Evolução Estelar
Evolução Estelar
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 22 abril 2008
![]() [Eugene Paul Wigner (1902-1995) e Fredrick Seitz (1911-2008)], de modo que
[Eugene Paul Wigner (1902-1995) e Fredrick Seitz (1911-2008)], de modo que
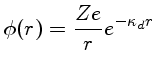
![\kappa_d = [\frac{4\pi e^2}{kT}(Z^2n_i+n_e)]^{1/2}](img7.gif)
![]()