Utilizando a relação entre o tempo próprio (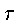 =tempo no
sistema de repouso na coordenada
=tempo no
sistema de repouso na coordenada 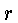 ) e a coordenada temporal
) e a coordenada temporal 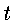 ,
podemos calcular a diferença entre a frequência emitida
em
,
podemos calcular a diferença entre a frequência emitida
em 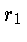 e a frequência recebida em um ponto qualquer
e a frequência recebida em um ponto qualquer 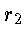 que é dada por
Podemos aproximar esta relação para um ponto
que é dada por
Podemos aproximar esta relação para um ponto
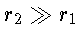 como
e, se o campo gravitacional for fraco
de modo que
e
É necessário identificar r1 = R como o raio da estrela, isto é,
a posição em que a radiação foi emitida. Este avermelhamento
gravitacional causa um deslocamento Doppler no centro das linhas
espectrais equivalente a
Multiplicando-se e dividindo-se pela massa e pelo raio do Sol,
obtemos:
como
e, se o campo gravitacional for fraco
de modo que
e
É necessário identificar r1 = R como o raio da estrela, isto é,
a posição em que a radiação foi emitida. Este avermelhamento
gravitacional causa um deslocamento Doppler no centro das linhas
espectrais equivalente a
Multiplicando-se e dividindo-se pela massa e pelo raio do Sol,
obtemos:
vgr = 0,635
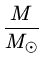
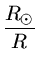
km/s
Para Sírius B, com
M = (1,053±0,028)M , obtém-se
vgr = (89±16) km/s.
, obtém-se
vgr = (89±16) km/s.
O desvio da luz α por um corpo gravitacional de potencial φ
pode ser calculado sabendo-se a distância de maior aproximação r
como
α=4GM/r
onde M é a massa total do sistema.
 Astronomia e Astrofísica
Astronomia e Astrofísica

Próxima: Tolman-Oppenheimer-Volkoff
Volta: Interiores Estelares
Anterior: Schwarzschild
©
Modificada em 10 nov 2001
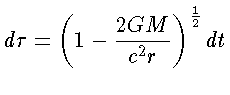
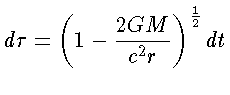
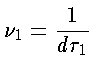
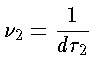
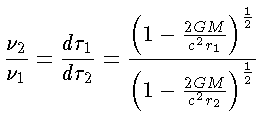
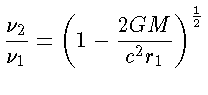
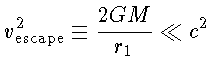
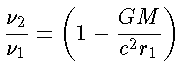
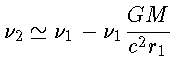
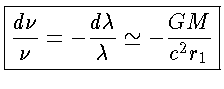
![]()