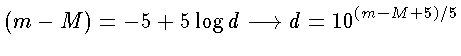
Uma das aplicações mais importantes do diagrama HR é a determinação de distâncias estelares. Suponha, por exemplo, que uma determinada estrela tem um espectro que indique que ela está na sequência principal e tem tipo espectral G2. Sua luminosidade então pode ser encontrada a partir do diagrama HR, e será em torno de 1 L⊙ (M = 4,72). Conhecendo-se sua magnitude aparente m, sua distância pode ser conhecida a partir do seu módulo de distância
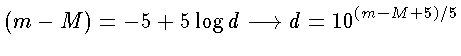
onde (m-M) é o módulo de distância, e
m = magnitude aparente
M = magnitude absoluta
d = distância em parsecs.
Em geral, a classe espectral sozinha não é suficiente para se
conhecer a luminosidade da estrela de forma única. É necessário
conhecer também sua classe de luminosidade.
Por exemplo, um estrela de tipo espectral G2 pode ter uma luminosidade
de
![]() , se for da sequência principal (M = 4,72), ou de
, se for da sequência principal (M = 4,72), ou de
![]() (M = 0), se for uma gigante, ou ainda de
(M = 0), se for uma gigante, ou ainda de
![]() (M = -5),
se for uma supergigante.
(M = -5),
se for uma supergigante.
Esta maneira de se obter as distâncias das estrelas, a partir do seu tipo espectral e da sua classe de luminosidade, é chamada método das paralaxes espectroscópicas.
| Tipo | (B - V)0 | (U - B)0 | Tef | C.B. | MV | Massa
( |
|---|---|---|---|---|---|---|
| O5 | -0,35 | -1,15 | 40000 | 4,00 | -5,8 | 120 |
| B0 | -0,31 | -1,06 | 28000 | 2,80 | -4,1 | 17 |
| B5 | -0,16 | -0,55 | 15500 | 1,50 | -1,1 | 6 |
| A0 | 0,00 | -0,02 | 9900 | 0,40 | 0,7 | 2,9 |
| A5 | 0,13 | 0,10 | 8500 | 0,12 | 2,0 | 2,2 |
| F0 | 0,27 | 0,07 | 7400 | 0,06 | 2,6 | 1,6 |
| F5 | 0,42 | 0,03 | 6580 | 0,00 | 3,4 | 1,25 |
| G0 | 0,58 | 0,05 | 6030 | 0,03 | 4,4 | 1,1 |
| G5 | 0,70 | 0,19 | 5520 | 0,07 | 5,1 | 0,9 |
| K0 | 0,89 | 0,47 | 4900 | 0,19 | 5,9 | 0,8 |
| K5 | 1,18 | 1,10 | 4130 | 0,60 | 7,3 | 0,65 |
| M0 | 1,45 | 1,18 | 3480 | 1,19 | 9,0 | 0,5 |
| M5 | 1,63 | 1,20 | 2800 | 2,30 | 11,8 | 0,15 |