Como se calcula o comprimento da sombra?
Consideremos um corpo luminoso de raio R a uma distância d de uma
esfera opaca de raio R'.
Por semelhança de triângulos temos que:
E portanto a altura do cone de sombra (L) é:
Onde:
- L = comprimento da sombra
- d = distância da fonte à esfera opaca
- R' = raio da esfera opaca
- R = raio da fonte

Como se calcula o raio da sombra da Terra à distância da Lua?

- L = comprimento da sombra
- R' = raio da Terra
- r(l) = raio da sombra a uma distância l da Terra
Novamente por semelhança de triângulos temos que:
E o raio da sombra à distância l da esfera opaca é:

Exemplos de cálculos de eclipses
- Calcular o comprimento médio da sombra da Terra,
considerando-se:
- distância Terra-Sol: 149 600 000 km
- raio da Terra: 6370 km
- raio do Sol: 696 000 km
Como
|
comprimento da sombra = |
distância da fonte × raio da esfera
raio da fonte -
raio da esfera
|
|
|
Obtemos:
|
comprimento da sombra = |
149 600 000 km × 6370 km
696 000 km
- 6370 km
|
|
|
ou
|
comprimento da sombra = 1 381 800 km |
|
- Seja r o raio da Terra, R = 109r o raio do Sol,
d = 23680r a distância entre o Sol e a Terra.
- a) Qual é o comprimento do cone de sombra formado?
|
L = |
d × r
R-r
|
= |
23680 r2
109r-r
|
= 219,26r |
|
- b) Qual é o raio deste cone a uma distância de l = 60r
por onde passa a Lua?
Como
|
r(l) = |
r
L
|
(L-l) = |
r
219,26r
|
(219,26r-60r) = 0,726 r |
|
- c) Sendo rL = r/3,6 o raio da Lua, quantos diâmetros
lunares cabem nessa região da sombra?
|
r(l)/rL = |
0,726 r
r / 3,6
|
= 2,6 |
|
Isto é, na distância da Lua, a umbra da Terra tem 9200 km. A penumbra
tem 16 000 km e como a velocidade da Lua na sua órbita é de
3400 km/hr, um eclipse total da Lua dura cerca de 1h 40m e um eclipse
parcial da Lua dura cerca de 6 h.
A duração e forma dos eclipses dependem da distância instantânea do
Sol e da Lua, que variam devido às órbitas elípticas, e também
dos ângulos no momento do eclipse, que variam devido à inclinação da órbita
da Terra em torno do Sol (obliqüidade da eclíptica=23,5°), e da inclinação
da órbita da Lua (5,2°).
 Órbita dos Planetas
Órbita dos Planetas
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 25 ago 2008


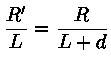
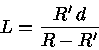


![]() Órbita dos Planetas
Órbita dos Planetas![]() Astronomia e Astrofísica
Astronomia e Astrofísica![]()